Baccalauréat S Asie 21 juin 2018 - Correction Spécialité
Page 10 sur 10
Correction de l'exercice de Spécialité 5 points
On s'intéresse à la figure suivante, dans laquelle $a$, $b$ et $c$ désignent les longueurs des hypoténuses des trois triangles rectangles en O dessinés ci-dessous. 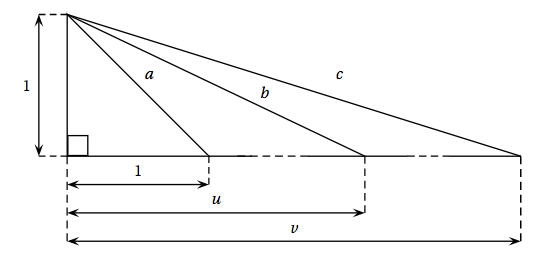
Problème :on cherche les couples de nombres entiers naturels non nuls $(u,~v)$ tels que $ab = c$.
- Modélisation : Démontrer que les solutions du problème sont des solutions de l'équation : \[(E) :\quad v^2 - 2u^2 = 1\quad (v \text{ et }\: u \: \text{ étant des entiers naturels non nuls}).\] On applique le théorème de Pythagore dans le triangle rectangle en $O$ d’hypoténuse de longueur $a$.
- Recherche systématique de solutions de l'équation $(E)$ Recopier et compléter l'algorithme suivant pour qu'il affiche au cours de son exécution tous les couples solutions de l'équation pour lesquels $1 \leqslant u \leqslant 1\;000 $ et $1 \leqslant v \leqslant 1\;000 $. $$\begin{array}{ |l |l| }\hline \text{Pour } u \text{ allant de 1 à } \ldots \text{ faire }& \text{ Au cours de son exécution,}\\ \hspace{0.5cm}\text{Pour } \ldots& \text{ l'algorthme affiche : }\\ \hspace{1cm}\text{ Si }\ldots& 2 \quad 3\\ \hspace{1.5cm}\text{Afficher } u \text{ et } v &12 \quad 17\\ \hspace{1cm}\text{ Fin Si } &70 \quad 99\\ \hspace{0.5cm}\text{ Fin Pour }&408 \quad 577\\ \text{Fin Pour }&\\ \hline \end{array}$$ $$\begin{array}{ |l |l| }\hline \text{Pour } u \text{ allant de 1 à } 1~000 \text{ faire }& \text{ Au cours de son exécution,}\\ \hspace{0.5cm}\text{Pour } v \text{ allant de 1 à } 1~000 \text{ faire }& \text{ l'algorthme affiche : }\\ \hspace{1cm}\text{ Si }v^2-2u^2=1& 2 \quad 3\\ \hspace{1.5cm}\text{Afficher } u \text{ et } v &12 \quad 17\\ \hspace{1cm}\text{ Fin Si } &70 \quad 99\\ \hspace{0.5cm}\text{ Fin Pour }&408 \quad 577\\ \text{Fin Pour }&\\ \hline \end{array}$$
- Analyse des solutions éventuelles de l'équation $(E)$ On suppose que le couple $(u,~v)$ est une solution de l'équation $(E)$.
- Établir que $u < v$. Si le couple $(u,v)$ est une solution de l’équation $(E)$ et que $u \geq v$ alors $2u^2>2v^2$.
- Démontrer que $n$ et $n^2$ ont la même parité pour tout entier naturel $n$. Supposons que $n$ soit pair. Il existe alors un entier naturel $k$ tel que $n=2k$.
- Démontrer que $v$ est un nombre impair. On considère un couple solution $(u,v)$ du problème.
- Établir que $2u^2 =(v-1)(v+1)$. En déduire que $u$ est un nombre pair. On a $v^2-2u^2=1 \iff 2u^2=v^2-1 \iff 2u^2=(v-1)(v+1)$.
Ainsi $2u^2 > v^2$ et $v^2-2u^2<0$.
Cela contredit le fait $v^2-2u^2=1$.
Par conséquent $u<v$.
$\quad$
Par conséquent $n^2=(2k)^2=4k^2=2\left(2k^2\right)$ et $n^2$ est pair.
Supposons que $n$ soit impair. Il existe alors une entier naturel $k$ tel que $n=2k+1$.
Alors $n^2=(2k+1)^2=4k^2+4k+1=2\left(2k^2+2k\right)+1$ et $n^2$ est impair.
Donc $n$ et $n^2$ ont la même parité.
$\quad$
Alors $v^2-2u^2=1 \iff v^2=2u^2+1$.
$v^2$ est donc impair. Par conséquent, d’après la question précédente $v$ l’est aussi.
$\quad$
$v$ est impair donc $v-1$ et $v+1$ sont pairs.
Il existe ainsi un entier naturel $k$ tel que $v-1=2k$ et $v+1=2(k+1)$.
Alors $2u^2=2k\times 2(k+1) \iff u^2=2k(k+1)$.
$u^2$ est donc pair.
D’après la question 3.b. $u$ est par conséquent pair.
$\quad$ - Une famille de solutions On assimile un couple de nombres entiers $(u,~v)$ à la matrice colonne $X = \begin{pmatrix}u\\v\end{pmatrix}$. On définit également la matrice $A = \begin{pmatrix}3&2\\4&3\end{pmatrix}$.
- Démontrer que si une matrice colonne $X$ est une solution de l'équation $(E)$, alors $AX$ est aussi une solution de l'équation $(E)$. Soit $X$ est une solution de l’équation $(E)$.
- Démontrer que si une matrice colonne $X$ est une solution de l'équation $(E)$, alors pour tout entier naturel $n$, $A^n X$ est aussi une solution de l'équation $(E)$. Montrons à l’aide d’un raisonnement par récurrence sur $n$ que si une matrice colonne $X$ est une solution de l’équation $(E)$ alors $A^nX$ est aussi une solution de l’équation $(E)$.
- À l'aide de la calculatrice, donner un couple $(u,~v)$ solution de l'équation $(E)$ tel que $v > 1\;0000 $. $3^2-2\times 2^2=9-8=1$.
$AX=\begin{pmatrix} 3u+2v\\4u+3v\end{pmatrix}$.
$\begin{align*} (4u+3v)^2-2(3u+2v)^2&=16u^2+9v^2+24uv-2\left(9u^2+4v^2+12uv\right) \\
&=16u^2+9v^2+24uv-18u^2-8v^2-24uv \\
&=v^2-2u^2\\
&=1
\end{align*}$
$AX$ est donc une solution de l’équation $(E)$.
$\quad$.
On suppose que la matrice colonne $X$ est une solution de l’équation $(E)$
Initialisation : si $n=0$ alors $A^nX=X$ et donc $A^nX$ est une solution de l’équation $(E)$.
La propriété est vraie au rang $0$.
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$ : $A^nX$ est aussi une solution de l’équation $(E)$.
Montrons qu’elle est encore vraie au rang suivant, c’est-à-dire que $A^{n+1}X$ est une solution de l’équation $(E)$.
$A^{n+1}X=A\left(A^nX\right)$.
$A^nX$ est aussi une solution de l’équation $(E)$ donc d’après la question précédente $A\left(A^nX\right)$ est également une solution de l’équation $(E)$.
la propriété est vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent pour tout entier naturel $n$ la matrice colonne $A^nX$ est aussi une solution de l’équation $(E)$.
$\quad$
Le couple $(2;3)$ est une solution de l’équation $(E)$.
On obtient $A^5X=\begin{pmatrix} 13~860\\19~601\end{pmatrix}$.
D’après la question précédente, le couple $(13~860;19~601)$ est solution de l’équation $(E)$ et $v>10~000$.
$\quad$
On obtient alors : $a^2=1^2+1^1=2$.
On faisant de même dans les deux autres triangles rectangles on peut écrire :
$b^2=1^2+u^2=1+u^2$ et $c^2=1^2+v^2=1+v^2$.
$\quad$
Si $ab=c$ alors $a^2b^2=c^2$.
Par conséquent $2\left(1+u^2\right)=1+v^2$
Soit $2+2u^2=1+v^2$
Et donc $v^2-2u^2=1$.
$\quad$
Les solutions du problème sont par conséquent également les solutions $(u,v)$ de l’équation $(E) : v^2-2u^2=1$ où $u$ et $v$ sont des entiers naturels non nuls.
$\quad$
- Vues: 29025
