Baccalauréat S Nouvelle-Calédonie Wallis et Futuna 28 novembre 2017 - Correction Exercice 1

Page 2 sur 12: Correction Exercice 1

Correction de l'exercice 1 (4 points)

Commun à tous les candidats

Sofia souhaite se rendre au cinéma. Elle peut y aller à vélo ou en bus.

Partie A : En utilisant le bus

On suppose dans cette partie que Sofia utilise le bus pour se rendre au cinéma. La durée du trajet entre son domicile et le cinéma (exprimée en minutes) est modélisée par la variable aléatoire $T_B$ qui suit la loi uniforme sur $[12~;~15]$.

1. Démontrer que la probabilité que Sofia mette entre $12$ et $14$ minutes est de $\dfrac23$.
On veut calculer $p\left(12 \leq T_B \leq 14\right)=\dfrac{14-12}{15-12}=\dfrac{2}{3}$
$\quad$
2. Donner la durée moyenne du trajet.
La durée moyenne du trajet est $E\left(T_B\right)=\dfrac{12+15}{2}=13,5$ min $=13$min $30$s
$\quad$

 

Partie B : En utilisant son vélo

On suppose à présent que Sofia choisit d'utiliser son vélo. La durée du parcours (exprimée en minutes) est modélisée par la variable aléatoire $T_v$ qui suit la loi normale d'espérance $\mu = 14$ et d'écart-type $\sigma=1,5$.

1. Quelle est la probabilité que Sofia mette moins de $14$ minutes pour se rendre au cinéma ? Quelle est la probabilité que Sofia mette entre $12$ et $14$ minutes pour se rendre au cinéma ? On arrondira le résultat à $10^{-3}$.
On veut calculer $p\left(T_V\leq 14\right)=0,5$ car $\mu=14$.
$\quad$
2. Démontrer que la probabilité, arrondie à $10^{-2}$, que Sofia mette entre $12$ et $14$ minutes est de $0,49$.
D’après la calculatrice $p\left(12\leq Tv\leq 14\right)\approx 0,409$
$\quad$

2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$

$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$

 

 

Partie C : En jouant aux dés

Sofia hésite entre le bus et le vélo. Elle décide de lancer un dé équilibré à $6$ faces. Si elle obtient $1$ ou $2$, elle prend le bus, sinon elle prend son vélo. On note :

• $B$ l'évènement « Sofia prend le bus » ;
• $V$ l'évènement « Sofia prend son vélo » ;
• $C$ l'évènement « Sofia met entre 12 et 14 minutes pour se rendre au cinéma ».

 

1. Sachant que Sofia a mis entre $12$ et $14$ minutes pour se rendre au cinéma, quelle est la probabilité, arrondie à $10^{-2}$, qu'elle ait emprunté le bus ?
La probabilité d’obtenir 1 ou 2 avec le dé est $\dfrac{2}{6}=\dfrac{1}{3}$.
Un arbre pondéré représentant la situation est donc :
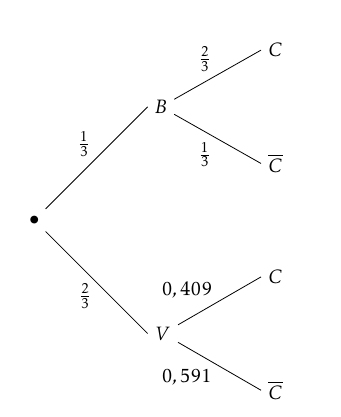D’après la formule des probabilités totales on a :
$\begin{align*} p(C)&=p(B\cap C)+p(V\cap V)\\
&=\dfrac{1}{3}\times \dfrac{2}{3}+\dfrac{2}{3}\times 0,409 \\
&\approx 0,49
\end{align*}$