Baccalauréat S Antilles-Guyane 11 septembre 2013 - Correction de l'Exercice 2

Page 4 sur 10: Correction de l'Exercice 2

Exercice 2 6 points

Commun à tous les candidats

Pour tout réel $k$ strictement positif, on désigne par $f_{k}$ la fonction définie et dérivable sur l'ensemble des nombres réels $\mathbb{R}$ telle que :
\[f_{k}(x) = kx\text{e}^{-kx}.\] On note $\mathcal{C}_{k}$ sa courbe représentative dans le plan muni d'un repère orthogonal $\left(\text{O}, \vec{i}, \vec{j}\right)$.
Partie A : Étude du cas $k = 1$
On considère donc la fonction $f_{1}$ définie sur $\mathbb{R}$ par
\[f_{1}(x) = x\text{e}^{- x}.\]

1. Déterminer les limites de la fonction $f_{1}$ en $- \infty$ et en $+ \infty$. En déduire que la courbe $\mathcal{C}_{1}$ admet une asymptote que l'on précisera.
$\left.\begin{array}{l} \lim\limits_{x \to \1}~\2=\3\\ \lim\limits_{x \to \1}~\4=\5 \end{array}\right\}$ par \8 on obtient: $\lim\limits_{x \to \1}~\6=\7$ $f_1(x) = x\text{e}^{-x}=\dfrac{x}{\text{e}^{x}}$ D'après une limite usuelle , on a $\lim\limits_{x\rightarrow +\infty}\dfrac{\text{e}^{x}}{x} =+\infty$, donc par inverse on obtient : $\lim\limits_{x\rightarrow +\infty}\dfrac{x}{\text{e}^{x}} =0$
   Comme  $\lim\limits_{x\rightarrow +\infty}f_1(x) = 0$; la courbe $\mathcal{C}_1$ possède donc une asymptote horizontale d’équation $y=0$ au voisinage de $+\infty$.

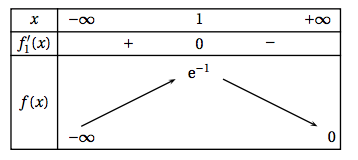
2. Étudier les variations de $f_{1}$sur $\mathbb{R}$ puis dresser son tableau de variation sur $\mathbb{R}$.

$\1 $ est dérivable comme produit de deux fonctions dérivables : 

$\1=uv$ d'où $\1'=u' v+uv' $ avec pour tout réel $x$, dans $D_ \{ \1\}$ :
$$\left\{ \begin{array}{l} u(x)~ =\2 \\ v(x)~ =\3 \end{array}\right.$$ d'où : $$\left\{ \begin{array}{l} u'(x)~ =\4 \\ v'(x)~ =\5 \end{array}\right.$$

Ainsi :
 $$\1'(x)=\left(\4\right) \times \left( \3\right) +\left(\5\right) \times \left( \2\right)$$


$$f_1'(x)=(1-x)\text{e}^{-x}$$
Comme la fonction exponentielle est strictement positive sur $\mathbb{R}$ ; le signe de $f_1′(x)$ ne dépend que de celui de $1-x$. On obtient donc le tableau de variations suivant :


3. Démontrer que la fonction $g_{1}$ définie et dérivable sur $\mathbb{R}$ telle que : \[g_{1}(x) = - (x + 1)\text{e}^{- x}\] est une primitive de la fonction $f_{1}$ sur $\mathbb{R}$.

$\1 $ est dérivable comme produit de deux fonctions dérivables : 

$\1=uv$ d'où $\1'=u' v+uv' $ avec pour tout réel $x$, dans $D_ \{ \1\}$ :
$$\left\{ \begin{array}{l} u(x)~ =\2 \\ v(x)~ =\3 \end{array}\right.$$ d'où : $$\left\{ \begin{array}{l} u'(x)~ =\4 \\ v'(x)~ =\5 \end{array}\right.$$

Ainsi :
 $$\1'(x)=\left(\4\right) \times \left( \3\right) +\left(\5\right) \times \left( \2\right)$$


$$g_1'(x)=(-1+x+1)\text{e}^{-x}=x\text{e}^{-x}=f_1(x)$$
$g_1$ est donc bien une primitive de $f_1$ sur $\mathbb{R}$.
4. Étudier le signe de $f_{1}(x)$ suivant les valeurs du nombre réel $x$.
Comme la fonction exponentielle est strictement positive sur $\mathbb{R}$ ; $f_1(x)$ est du signe de $x$. Donc $f_1(x) < 0$ sur $]-\infty;0[$, $f_1(x) > 0$ sur $]0;+\infty[$ et $f_1(0)=0$.
5. Calculer, en unité d'aire, l'aire de la partie du plan délimitée par la courbe $\mathcal{C}_{1}$, l'axe des abscisses et les droites d'équation $x = 0$ et $x = \ln 10$.
L'aire demandée correspond donc à :
$$\int_0^{\text{ln }10} f_1(x)\text{d}x = \left[-(x+1)\text{e}^{-x}\right]_0^{\text{ln } 10} = – \dfrac{\text{ln }(10) + 1}{10} + 1 = \dfrac{9 – \text{ln }(10)}{10} ~\text{u.a.}$$

Partie B : Propriétés graphiques

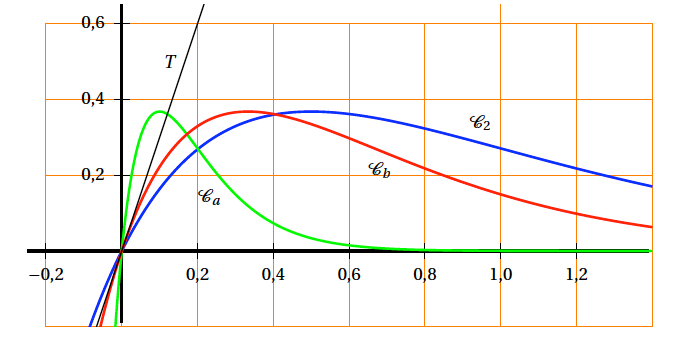
On a représenté sur le graphique ci-dessous les courbes $\mathcal{C}_{2}$, $\mathcal{C}_{a}$ et $\mathcal{C}_{b}$ où $a$ et $b$ sont des réels strictement positifs fixés et T la tangente à $\mathcal{C}_{b}$ au point O origine du repère.

1. Montrer que pour tout réel $k$ strictement positif, les courbes $\mathcal{C}_{k}$ passent par un même point.
$f_1(x) = kx\text{e}^{-kx}$ donc $f_k(0)=0$.
Par conséquent toutes les courbes $\mathcal{C}_k$ passent par l’origine du repère.
2. 1. Montrer que pour tout réel $k$ strictement positif et tout réel $x$ on a \[f'_{k}(x) = k(1 - kx)\text{e}^{- kx}.\]

   $\1 $ est dérivable comme produit de deux fonctions dérivables : 

   $\1=uv$ d'où $\1'=u' v+uv' $ avec pour tout réel $x$, dans $D_ \{ \1\}$ :
   $$\left\{ \begin{array}{l} u(x)~ =\2 \\ v(x)~ =\3 \end{array}\right.$$ d'où : $$\left\{ \begin{array}{l} u'(x)~ =\4 \\ v'(x)~ =\5 \end{array}\right.$$

   Ainsi :
    $$\1'(x)=\left(\4\right) \times \left( \3\right) +\left(\5\right) \times \left( \2\right)$$

   
   $$f_k'(x)=k(1 - kx)\text{e}^{- kx}$$
   
   2. Justifier que, pour tout réel $k$ strictement positif, $f_{k}$ admet un maximum et calculer ce maximum.
   $f_k’(x)$ est donc du signe de $(1-kx)$.
   La fonction $f_k$ est par conséquent croissante sur $\left]-\infty;\dfrac{1}{k}\right]$ et croissante sur $\left[\dfrac{1}{k};+\infty\right[$.
   Elle admet donc un maximum en $\dfrac{1}{k}$ et $f_k\left(\dfrac{1}{k}\right)=\text{e}^{-1}$.
   
   3. En observant le graphique ci-dessus, comparer $a$ et 2. Expliquer la démarche.
   L’abscisse du sommet est $\dfrac{1}{k}$. Graphiquement, on constate que le sommet de $\mathcal{C}_a$ est situé, horizontalement, avant celui de $\mathcal{C}_2$.
   Par conséquent $a > 2$.
   
   4. Écrire une équation de la tangente à $\mathcal{C}_{k}$ au point O origine du repère.

   La tangente $\1$ à $\2$ au point d'abscisse $a= \3$ a pour équation : $$y=\6'(\3)(x-\3)+\6(\3)$$ Ici $a= \3$, on calcule successivement :

   • $\6\left(\3 \right)=\4$
   • $\6'\left (\3\right )=\5$

   Ainsi $\1:y=\5\left (x-\3\right )+\4$

   
   Une équation de la tangente en $O$ est donc $y= kx$.
   5. En déduire à l'aide du graphique une valeur approchée de $b$.
   On constate que le coefficient directeur de $T$ est environ $\dfrac{0,6}{0,2} = 3$. Donc $b=3$.