Baccalauréat S Pondichéry 16 avril 2013 - Correction de l'Exercice 3

Page 6 sur 11: Correction de l'Exercice 3

Exercice 3 5 points

Candidats n'ayant pas suivi l'enseignement de spécialité
Le plan complexe est muni d'un repère orthonormé direct $\left(O,\vec{u},\vec{v}\right)$. On note i le nombre complexe tel que $\text{i}^2 = - 1$.
On considère le point A d'affixe $z_{\text{A}} = 1$ et le point B d'affixe $z_{\text{B}} = \text{i}$.

À tout point $M$ d'affixe $z_{M} = x + \text{i}y$, avec $x$ et $y$ deux réels tels que $y \neq 0$, on associe le point $M'$ d'affixe $z_{M'} = - \text{i}z_{M}$.

On désigne par $I$ le milieu du segment [A$M$].

Le but de l'exercice est de montrer que pour tout point $M$ n'appartenant pas à (OA), la médiane (O$I$) du triangle OA$M$ est aussi une hauteur du triangle OB$M'$ (propriété 1)

et que B$M' = 2 \text{O}I$ (propriété 2).

1. Dans cette question et uniquement dans cette question, on prend
   $z_{M} = 2\text{e}^{- \text{i}\frac{\pi}{3}}$.
   1. Déterminer la forme algébrique de $z_{M}$.
   $Z_M = 2 \left( \cos \left(\dfrac{-\pi}{3}\right) + \text{i} \sin \left(\dfrac{-\pi}{3}\right) \right) = 1 – \text{i} \sqrt{3}$
   2. Montrer que $z_{M'} = - \sqrt{3} - \text{i}$.
   $Z_{M’} = -\text{i}\left(1 - \text{i}\sqrt{3} \right) = -\sqrt{3} - \text{i}$
   3. Déterminer le module et un argument de $z_{M'}$.
      • $|Z_{M’}| = |-\text{i}|\times |Z_M| = 1 \times 2 = 2$
      • $\text{arg }\left( Z_{M’}\right) = \text{arg }(-\text{i}) + \text{arg }\left(Z_M \right) = -\dfrac{\pi}{2} – \dfrac{\pi}{3} = \dfrac{-5\pi}{6} [2\pi]$
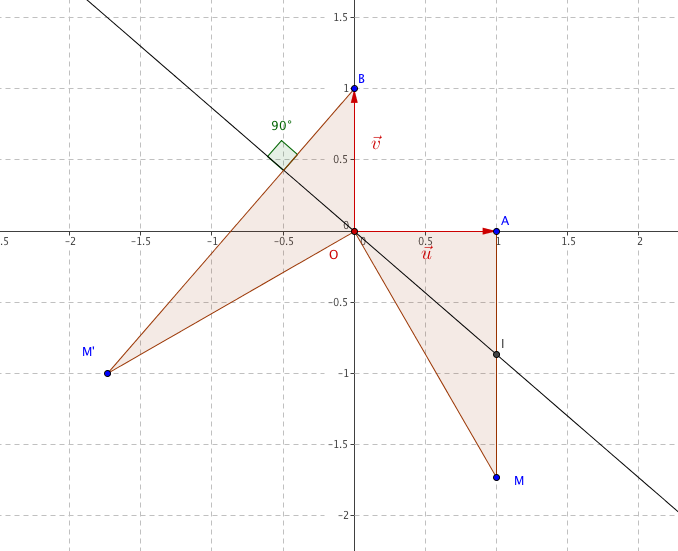
   4. Placer les points A, B, $M, M'$ et $I$ dans le repère $\left(O,\vec{u},\vec{v}\right)$ en prenant 2 cm pour unité graphique.
   
   5. Tracer la droite (O$I$) et vérifier rapidement les propriétés 1 et 2 à l'aide du graphique.
   On constate effectivement que la droite (OI) est bien perpendiculaire à ($M'$) et que B$M'$=2OI.
2. On revient au cas général en prenant $z_{M} = x + \text{i}y$ avec $y \neq 0$.
   1. Déterminer l'affixe du point $I$ en fonction de $x$ et $y$.
   $Z_I = \dfrac{Z_A+Z_M}{2} = \dfrac{1+x}{2} + \text{i}\dfrac{y}{2}$
   2. Déterminer l'affixe du point $M'$ en fonction de $x$ et $y$.
   $Z_{M’} = -\text{i}(x+iy) = -\text{i}x+y$
   3. Écrire les coordonnées des points $I$, B et $M'$.
   Par suite $I\left(\dfrac{1+x}{2};\dfrac{y}{2} \right)$ ; $B(0;1) $ et $M’(y;-x)$
   4. Montrer que la droite (O$I$) est une hauteur du triangle OB$M'$.
   Calculons le produit scalaire $\vec{OI}.\vec{BM’}=\dfrac{1+x}{2} \times y + \dfrac{y}{2} \times (-x-1) = 0;$ Donc (OI) est une hauteur de OB$M′$.
   5. Montrer que B$M' = 2 \text{O}I$.
      • $ BM’ = \sqrt{y^2+(-x-1)^2} = \sqrt{y^2+(x+1)^2}$
      • $OI = \sqrt{\left(\dfrac{1+x}{2} \right)^2 + \left(\dfrac{y}{2} \right)^2} = \dfrac{\sqrt{(1+x)^2+y^2}}{2}$
      • Donc B$M′$=2OI