Baccalauréat S Asie 20 juin 2019 - Correction Exercice 4
Page 8 sur 10
Correction de l'exercice 4 5 points
- On considère dans l'ensemble des nombres complexes l'équation $(E)$ à l'inconnue $z$ : \[z^3 + \left( -2\sqrt{3} + 2\text{i}\right) z^2 + \left(4 - 4\text{i}\sqrt{3}\right) z + 8\text{i} = 0\quad (E). \]
- Montrer que le nombre $-2\text{i}$ est une solution de l'équation $(E)$. $\begin{align*} &(-2\text{i})^3+\left(-2\sqrt{3}+2\text{i}\right)\times (-2\text{i})^2+\left(4-4\text{i}\sqrt{3}\right)\times (-2\text{i})+8\text{i}\\
- Vérifier que, pour tout nombre complexe $z$, on a : \[z^3 + \left( -2\sqrt{3} + 2\text{i}\right) z^2 + \left(4 - 4\text{i}\sqrt{3}\right) z + 8\text{i} = (z + 2i)\left(z^2 - 2\sqrt{3} z + 4\right).\] On a :
- Résoudre l'équation $(E)$ dans l'ensemble des nombres complexes. Un produit de facteurs est nul si, et seulement si, un de ses facteurs au moins est nul.
- Écrire les solutions de l'équation $(E)$ sous forme exponentielle. $-2\text{i}=2\text{e}^{-\text{i}\pi/2}$
=& 8\text{i} -4\left(-2\sqrt{3}+2\text{i}\right)-\left(8\text{i}+8\sqrt{3}\right)+8\text{i}\\
=& 8\text{i}+8\sqrt{3}-8\text{i}-8\text{i}-8\sqrt{3}+8\text{i}\\
=& 0\end{align*}$
$-2\text{i}$ est donc une solution de l’équation $(E)$.
$\quad$
$\begin{align*}& (z+2\text{i})\left(z^2-2\sqrt{3}z+4\right)\\
=& z^3-2\sqrt{3}z^2+4z+2\text{i} z^2-4\text{i}\sqrt{3}z+8\text{i} \\
=& z^3+\left(2\text{i}-2\sqrt{3}\right)z^2+\left(4-4\text{i}\sqrt{3}\right)z+8\text{i}\end{align*}$
$\quad$
Donc $(E)\iff z+2\text{i}=0$ ou $z^2-2\sqrt{3}z+4=0$
$z+2\text{i} =0\iff z=-2\text{i}$
On considère maintenant l’équation $z^2-2\sqrt{3}z+4=0$
$\Delta=\left(-2\sqrt{3}\right)^2-4\times 1\times 4=-4<0$
Les solutions de cette équation sont donc :
$z_1=\dfrac{2\sqrt{3}-2\text{i}}{2}=\sqrt{3}-\text{i}$ et $z_2=\overline{z_1}=\sqrt{3}+\text{i}$
Ainsi les solutions de l’équation $(E)$ sont $-2\text{i}$, $\sqrt{3}+\text{i}$ et $\sqrt{3}-\text{i}$.
$\quad$
$\left|\sqrt{3}+\text{i}\right|=2$ donc $\sqrt{3}+\text{i}=2\left(\dfrac{\sqrt{3}}{2}+\dfrac{\text{i}}{2}\right)=2\text{e}^{\text{i}\pi/6}$
et $\sqrt{3}-\text{i}=2\text{e}^{-\text{i}\pi/6}$
$\quad$
Dans la suite, on se place dans le plan muni d'un repère orthonormé direct d'origine $O$.
- On considère les points A, B, C d'affixes respectives $-2i$, $\sqrt{3} + \text{i}$ et $\sqrt{3} - \text{i}$.
- Montrer que A, B et C appartiennent à un même cercle de centre O dont on déterminera le rayon. Les trois nombres complexes sont tous de module $2$.
- Placer ces points sur une figure que l'on complètera par la suite. Voir figure en fin d’exercice
- On note D le milieu du segment [OB]. Déterminer l'affixe $z_{\text{L}}$ du point L tel que AODL soit un parallélogramme. $D$ est le milieu du segment $[OB]$.
Par conséquent $OA=OB=OC=2$.
Les points $A$, $B$ et $C$ appartiennent donc au cercle de centre $O$ et de rayon $2$.
$\quad$
$\quad$
Ainsi $z_D=\dfrac{z_O+z_B}{2}=\dfrac{\sqrt{3}}{2}+\dfrac{\text{i}}{2}$.
$\quad$
$AODL$ est un parallélogramme
$\iff \vec{AL}=\vec{OD}$
$\iff z_L-z_A=z_D-z_O$
$\iff z_L=z_D+z_A$
$\iff z_L=\dfrac{\sqrt{3}}{2}+\dfrac{\text{i}}{2}-2\text{i}$
$\iff z_L=\dfrac{\sqrt{3}}{2}-\dfrac{3\text{i}}{2}$
$\quad$ - On rappelle que, dans un repère orthonormé du plan, deux vecteurs de coordonnées respectives $(x~;~y)$ et $(x'~;~y')$ sont orthogonaux si et seulement si $xx'+yy' = 0$.
- Soit $\vec{u}$ et $\vec{v}$ deux vecteurs du plan, d'affixes respectives $z$ et $z'$. Montrer que $\vec{u}$ et $\vec{v}$ sont orthogonaux si et seulement si $z \overline{z'}$ est un imaginaire pur. On note $z=x+\text{i} y$ et $z’=x’+\text{i} y’$.
- À l'aide de la question 3. a. , démontrer que le triangle AOL est rectangle en L. L’affixe du vecteur $\vec{OL}$ est $z=\dfrac{\sqrt{3}}{2}-\dfrac{3\text{i}}{2}$
Ainsi
$\begin{align*} z\overline{z’}&=(x+\text{i} y)\left(x’-\text{i} y’\right)\\
&=xx’-\text{i} xy’+\text{i} yx’+yy’ \\
&=xx’+yy’+(x’y-xy’)\text{i}\end{align*}$
Par conséquent :
$z\overline{z’}$ est un imaginaire pur
$\iff xx’+yy’=0$
$\iff \vec{u}$ et $\vec{v}$ sont orthogonaux
$\quad$
L’affixe du vecteur $\vec{AL}$ est $z’=\dfrac{\sqrt{3}}{2}-\dfrac{3\text{i}}{2}+2\text{i}=\dfrac{\sqrt{3}}{2}-\dfrac{3\text{i}}{2}+\dfrac{\text{i}}{2}$.
Ainsi :
$\begin{align*} z\overline{z’}&=\left(\dfrac{\sqrt{3}}{2}-\dfrac{3\text{i}}{2}\right)\left(\dfrac{\sqrt{3}}{2}-\dfrac{\text{i}}{2}\right) \\
&=\dfrac{3}{4}-\dfrac{\sqrt{3}\text{i}}{4}-\dfrac{3\text{i}\sqrt{3}}{4}-\dfrac{3}{4} \\
&=-\text{i}\sqrt{3}\end{align*}$
$z\overline{z’}$ est donc un imaginaire pur. Les vecteurs $\vec{OL}$ et $\vec{AL}$ sont donc orthogonaux et le triangle $AOL$ est rectangle en $L$.
$\quad$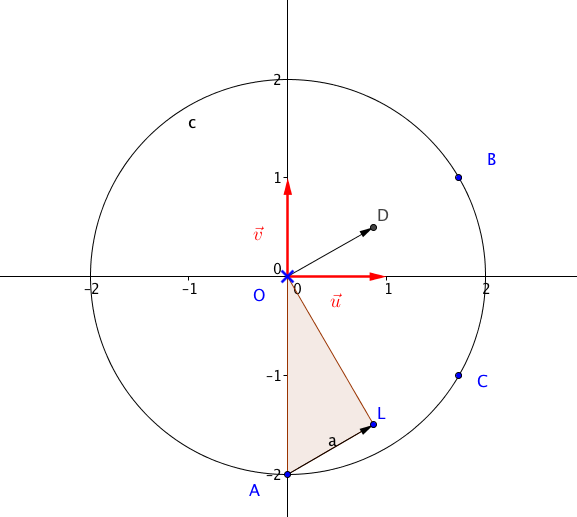
- Vues: 105681
