Baccalauréat S Polynésie 19 juin 2019 - Correction Exercice 4
Page 8 sur 10
Correction de l'exercice 4 5 points
Sur la figure donnée en annexe 2 à rendre avec la copie :
- ABCDEFGH est un parallélépipède rectangle tel que AB $= 12$, AD $= 18$ et AE $= 6$
- EBDG est un tétraèdre.
L'espace est rapporté à un repère orthonormal d'origine A dans lequel les points B, D et E ont pour coordonnées respectives B(12 ; 0 ; 0), D(0 ; 18 ; 0) et E(0 ; 0 ; 6).
- Démontrer que le plan (EBD) a pour équation cartésienne $3x + 2y + 6z - 36 = 0$. Montrons que les coordonnées des points $E, B$ et $D$ sont solutions de l’équation fournie.
-
- Déterminer une représentation paramétrique de la droite (AG). On a $\vec{AG}(12;18;6)$.
- En déduire que la droite (AG) coupe le plan (EBD) en un point K de coordonnées (4 ; 6 ; 2) . Prenons $t=\dfrac{1}{3}$. On a alors $\begin{cases} 12t=4\\18t=6\\6t=3\end{cases}$. Le point $K(4;6;3)$ appartient donc à la droite $(AG)$.
Ainsi une représentation paramétrique de la droite $(AG)$ est : $$\begin{cases} x=12t\\y=18t\\z=6t\end{cases} \quad, t\in\matbb R$$
$\quad$
De plus $3\times 4+2\times 6+6\times 2-36=12+12+12-36=0$.
Le point $K$ appartient également au plan $(EBD)$.
Un vecteur normal au plan $(EBD)$ est $\vec{n}(3;2;6)$
$\vec{n}.\vec{AG}=3\times 12+2\times 18+6\times 6=108\neq 0$. La droite $(AG)$ n’est donc pas incluse dans le plan $(EBD)$.
Ainsi la droite $(AG)$ coupe le plan $(EBD)$ en un point $K$ de coordonnées $(4;6;2)$.
$\quad$ - La droite (AG) est-elle orthogonale au plan (EBD) ? Justifier. On a $\vec{AG}(12;18;6)$ et $\vec{n}(3;2;6)$.
-
- Soit M le milieu du segment [ED]. Démontrer que les points B, K et M sont alignés. Le point $M$ est le milieu du segment $[ED]$.
- Construire alors le point K sur la figure donnée en annexe 2 à rendre avec la copie. Le point $K$ est donc le point d’intersection des droites $(AG)$ et $(BM)$.
Ainsi $x_M=\dfrac{0+0}{2}$, $y_M=\dfrac{18+0}{2}=9$ et $z_M=\dfrac{0+6}{2}=3$.
Les coordonnées du points $M$ sont donc $(0;9;3)$.
Par conséquent :
– les coordonnées du vecteur sont $\vec{BM}(-12;9;3)$;
– les coordonnées du vecteur sont $\vec{BK}(-8;6;2)$.
$\dfrac{-12}{-8}=1,5$, $\dfrac{9}{6}=1,5$ et $\dfrac{3}{2}=1,5$.
Cela signifie donc que $\vec{BM}=1,5\vec{BK}$.
Les deux vecteurs sont colinéaires et les points $B$, $M$ et $K$ sont alignés.
$\quad$
$\quad$ - On note P le plan parallèle au plan (ADE) passant par le point K.
- Démontrer que le plan P coupe le plan (EBD) selon une parallèle à la droite (ED). Les plans $(AED)$ et $(EBD)$ se coupent selon la droite $(ED)$.
- Construire alors sur l'annexe 2 à rendre avec la copie l'intersection du plan P et de la face EBD du tétraèdre EBDG.
Le plan $P$ est parallèle au plan $(AED)$ et passe par le point $K$.
Le point $K$ appartient donc aux plans $(EBD)$ et $P$.
Par conséquent l’intersection du plan $P$ et du plan $(EBD)$ est une droite parallèle à la droite $(ED)$ passant par le point $K$.
$\quad$
ANNEXE 2
L’intersection du plan $P$ et de la face $EBD$ est représentée en bleue.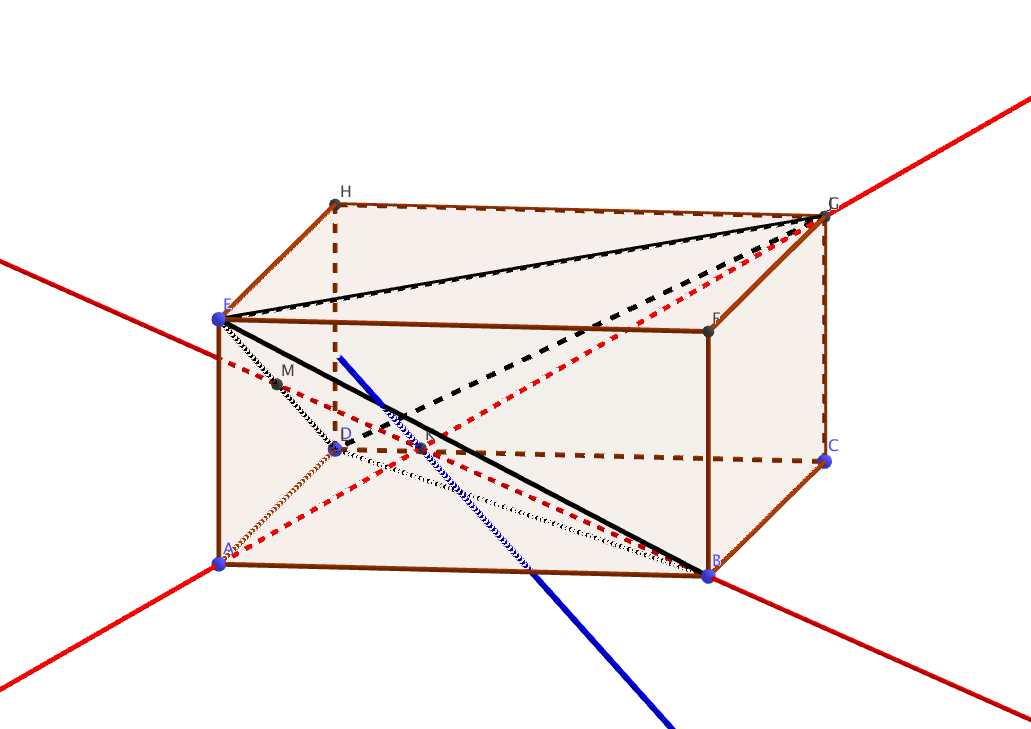
Pour le point $E$ : $3\times 0+2\times 0+6\times 6-36=36-36=0$.
Pour le point $B$ : $3\times 12+2\times 0+6\times 0-36=36-36=0$.
Pour le point $D$ : $3\times 0+2\times 18+6\times 0-36=36-36=0$.
Une équation cartésienne du plan $(EBD)$ est donc $3x+2y+6z-36=0$.
$\quad$
Ils ont la même troisième coordonnée mais les deux autres sont différentes. Ces deux vecteurs ne sont donc pas colinéaires et la droite $(AG)$ n’est pas orthogonale au plan $(EBD)$.
$\quad$
- Vues: 52570
