Rédigé par Luc Giraud le . Publié dans Annales S 2019.

Baccalauréat S Polynésie 19 juin 2019

 

 

Exercice 1 5 points


Commun à tous les candidats


Les probabilités demandées seront arrondies à 0,01.
Un commerçant vient de s'équiper d'un distributeur de glaces à l'italienne.

  1. La durée, en mois, de fonctionnement sans panne de son distributeur de glaces à l'italienne est modélisée par une variable aléatoire $X$ qui suit une loi exponentielle de paramètre $\lambda$ où $\lambda$ est un réel strictement positif (on rappelle que la fonction $f$de densité de la loi exponentielle est donnée sur $[0 ;  +\infty[$ par $f(x) = \lambda\text{e}^{- \lambda x}$. Le vendeur de l'appareil assure que la durée moyenne de fonctionnement sans panne de ce type de distributeur, c'est-à-dire l'espérance mathématique de $X$, est de $10$ mois.
    1. Justifier que $\lambda = 0,1$.
    2. Calculer la probabilité que le distributeur de glaces à l'italienne n'ait connu aucune panne pendant les six premiers mois.
    3. Sachant que le distributeur n'a connu aucune panne pendant les six premiers mois, quelle est la probabilité qu'il n'en connaisse aucune jusqu'à la fm de la première annéeb? Justifier.
    4. Le commerçant remplacera son distributeur de glaces à l'italienne au bout d'un temps $t$, exprimé en mois, qui vérifie que la probabilité de l'évènement $(X > t)$ est égale à $0,05$. Déterminer la valeur de $t$ arrondie à l'entier.
  2. La notice du distributeur de glaces précise que le distributeur fournit des glaces à l'italienne dont la masse est comprise entre 55 g et 65 g. On considère la variable aléatoire $M$ représentant la masse, en grammes, d'une glace distribuée. On admet que $M$ suit la loi normale d'espérance $60$ et d'écart-type $2,5$.
    1. Calculer la probabilité que la masse d'une glace à l'italienne choisie au hasard parmi celles distribuées soit comprise entre $55$ g et $65$ g.
    2. Déterminer la plus grande valeur de $m$, arrondie au gramme près, telle que la probabilité $P(M \geqslant m)$ soit supérieure ou égale à $0,99$.
  3. Le distributeur de glaces à l'italienne permet de choisir un seul des deux parfums: vanille ou fraise. Pour mieux gérer ses achats de matières premières, le commerçant fait l'hypothèse qu'il y aura en proportion deux acheteurs de glace à la vanille pour un acheteur de glace à la fraise. Le premier jour d'utilisation de son distributeur, il constate que sur $120$ consommateurs, $65$ ont choisi de la glace à la vanille. Pour quelle raison mathématique pourrait-il mettre en doute son hypothèse ? Justifier.

Correction de l'exercice 1 (5 points)


Commun à tous les candidats


Les probabilités demandées seront arrondies à 0,01.
Un commerçant vient de s'équiper d'un distributeur de glaces à l'italienne.

  1. La durée, en mois, de fonctionnement sans panne de son distributeur de glaces à l'italienne est modélisée par une variable aléatoire $X$ qui suit une loi exponentielle de paramètre $\lambda$ où $\lambda$ est un réel strictement positif (on rappelle que la fonction $f$de densité de la loi exponentielle est donnée sur $[0 ;  +\infty[$ par $f(x) = \lambda\text{e}^{- \lambda x}$. Le vendeur de l'appareil assure que la durée moyenne de fonctionnement sans panne de ce type de distributeur, c'est-à-dire l'espérance mathématique de $X$, est de $10$ mois.
    1. Justifier que $\lambda = 0,1$.
      2. D’après l’énoncé, on a $E(X)=10$.
      Or $E(X)=\dfrac{1}{\lambda}$ donc $\dfrac{1}{\lambda}=10 \iff \lambda =0,1$.
      $\quad$
    2. Calculer la probabilité que le distributeur de glaces à l'italienne n'ait connu aucune panne pendant les six premiers mois.
      3. On veut calculer $P(X\geq 6)=\text{e}^{-0,1\times 6}=\text{e}^{-0,6}\approx 0,55$.
      La probabilité que le distributeur de glaces à l’italienne n’ait connu aucune panne pendant les six premiers mois est environ égale à $0,55$.
      $\quad$
    3. Sachant que le distributeur n'a connu aucune panne pendant les six premiers mois, quelle est la probabilité qu'il n'en connaisse aucune jusqu'à la fm de la première année ? Justifier.
      4. La loi exponentielle est une loi à durée de vie sans vieillissement. Donc :
      $\begin{align*} P_{X\geq 6}(X\geq 12)&=P_{X\geq 6}(X\geq 6+6)\\
      &=P(X\geq 6)\\
      &=\text{e}^{-0,6}\\
      &\approx 0,55\end{align*}$.
      Sachant que le distributeur n’a connu aucune panne pendant les six premiers mois, la probabilité qu’il n’en connaisse aucune jusqu’à la fin de la première année est environ égale à $0,55$.
      $\quad$
    4. Le commerçant remplacera son distributeur de glaces à l'italienne au bout d'un temps $t$, exprimé en mois, qui vérifie que la probabilité de l'évènement $(X > t)$ est égale à $0,05$. Déterminer la valeur de $t$ arrondie à l'entier.
      5. On cherche à résoudre l’équation :
      $\begin{align*} P(X>t)=0,05 &\iff \text{e}^{-0,1t}=0,05 \\
      &\iff -0,1t=\ln 0,05\\
      &\iff t=-10\ln 0,05\end{align*}$
      Ainsi $t\approx 30$.
      $\quad$
  2. La notice du distributeur de glaces précise que le distributeur fournit des glaces à l'italienne dont la masse est comprise entre 55 g et 65 g. On considère la variable aléatoire $M$ représentant la masse, en grammes, d'une glace distribuée. On admet que $M$ suit la loi normale d'espérance $60$ et d'écart-type $2,5$.
    1. Calculer la probabilité que la masse d'une glace à l'italienne choisie au hasard parmi celles distribuées soit comprise entre $55$ g et $65$ g.
      2. On a $P(55 \leq M\leq 65)=P(\mu-2\sigma\leq M\leq \mu+2\sigma)\approx 0,95$.
      Remarque : On pouvait également retrouver cette valeur directement avec la calculatrice.
      $\quad$

      2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
      Avec une calculatrice de type TI

      $$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$

      $$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$

       

    2. Déterminer la plus grande valeur de $m$, arrondie au gramme près, telle que la probabilité $P(M \geqslant m)$ soit supérieure ou égale à $0,99$.
      3. On veut déterminer le réel $m$ tel que $P(M\geq m)\geq 0,99 \iff P(M\leq m)\leq 0,01$.
      À l’aide de la touche Inverse loi normale de la calculatrice on trouve $m\approx 54$.
      $\quad$

      2ND DISTR 2Fracnormale( \1 , \2, \3 )EXE
      Avec une calculatrice de type TI $FracNormale(\1,\2,\3) \approx \4$

      $$\Pi_{\2,\3}^{-1}(\1)\approx \4 \text{ à } 10^{-\5} \text{ près.}$$

       

  3. Le distributeur de glaces à l'italienne permet de choisir un seul des deux parfums: vanille ou fraise. Pour mieux gérer ses achats de matières premières, le commerçant fait l'hypothèse qu'il y aura en proportion deux acheteurs de glace à la vanille pour un acheteur de glace à la fraise. Le premier jour d'utilisation de son distributeur, il constate que sur $120$ consommateurs, $65$ ont choisi de la glace à la vanille. Pour quelle raison mathématique pourrait-il mettre en doute son hypothèse ? Justifier.
    4. On a $n=120$ et la probabilité théorique qu’un consommateur choisisse la glace à la vanille est $p=\dfrac{2}{3}$.
    Ainsi $n\geq 30$, $np=80\geq 5$ et $n(1-p)=40\geq 5$.
    Un intervalle de fluctuation asymptotique au seuil de $95\%$ de la proportion de consommateurs choisissant la glace à la vanille est :
    $\begin{align*} I_{120}&=\left[\dfrac{2}{3}-1,96\sqrt{\dfrac{\dfrac{2}{3}\times \dfrac{1}{3}}{120}};\dfrac{2}{3}+1,96\sqrt{\dfrac{\dfrac{2}{3}\times \dfrac{1}{3}}{120}}\right] \\
    &\approx [0,58;0,76]\end{align*}$
    La fréquence observée est $f=\dfrac{65}{120}\approx 0,54 \notin I_{120}$.
    Au risque d’erreur de $5\%$ cela remet en cause l’hypothèse faite par le commerçant.
    $\quad$

Exercice 2 5 points


Commun à tous les candidats


L'écoulement de l'eau d'un robinet a un débit constant et modéré.
robinet
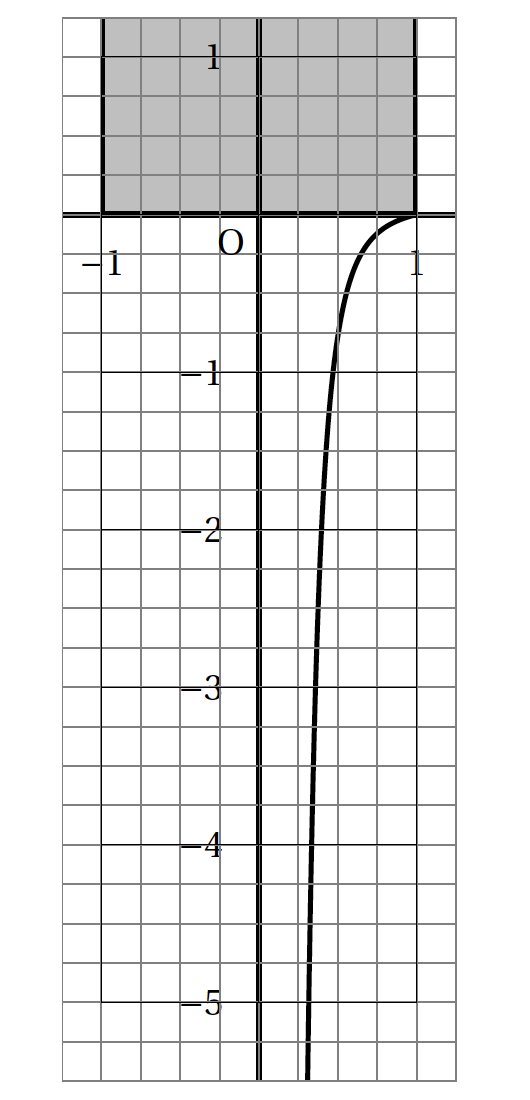
On s'intéresse en particulier à une partie du profil d'écoulement représentée en annexe 1 par la courbe $C$ dans un repère orthonormé.

Partie A


On considère que la courbe $C$ donnée en  annexe 1  est la représentation graphique d'une fonction $f$ dérivable sur l'intervalle ]0 ; 1] qui respecte les trois conditions suivantes: \[(H):\: f(1) = 0\qquad f'(1) = 0,25\quad \text{et} \:\: \displaystyle\lim_{\substack{x \to 0\\x > 0}} f(x) = - \infty.\]

  1. La fonction $f$ peut-elle être une fonction polynôme du second degré ? Pourquoi ?
  2. Soit $g$ la fonction définie sur l'intervalle ]0 ; 1] par $g(x) = k \ln x$.
    1. Déterminer le réel $k$ pour que la fonction $g$ respecte les trois conditions $(H)$.
    2. La courbe représentative de la fonction $g$ coïncide-t-elle avec la courbe $C$ ? Pourquoi ?
  3. Soit $h$ la fonction définie sur l'intervalle ]0 ; 1] par $h(x) = \dfrac{a}{x^4} + bx$ où $a$ et $b$ sont des réels. Déterminer $a$ et $b$ pour que la fonction $h$ respecte les trois conditions $(H)$.

 

Partie B


On admet dans cette partie que la courbe $C$ est la représentation graphique d'une fonction $f$continue, strictement croissante, définie et dérivable sur l'intervalle ]0 ; 1] d'expression: \[f(x) = \dfrac{1}{20}\left(x - \dfrac{1}{x^4} \right).\]

  1. Justifier que l'équation $f(x) = -5$ admet sur l'intervalle ]0 ; 1] une unique solution qui sera notée $\alpha$. Déterminer une valeur approchée de $\alpha$ à $10^{-2}$ près.
  2. On admet que le volume d'eau en cm$^3$, contenu dans les 5 premiers centimètres de l'écoulement, est donné par la formule : $$V = \displaystyle\int_{\alpha}^1\pi x^2 f'(x)\:\text{d}x.$$
    1. Soit $u$ la fonction dérivable sur ]0 ; 1] définie par $u(x) = \dfrac{1}{2x^2}$. Déterminer sa fonction dérivée.
    2. Déterminer la valeur exacte de $V$. En utilisant la valeur approchée de $\alpha$ obtenue à la question 1, donner alors une valeur approchée de $V$.
 Annexe 1
Courbe Ex1

Correction de l'exercice 2 (5 points)


Commun à tous les candidats


L'écoulement de l'eau d'un robinet a un débit constant et modéré.
robinet
On s'intéresse en particulier à une partie du profil d'écoulement représentée en annexe 1 par la courbe $C$ dans un repère orthonormé.

Partie A


On considère que la courbe $C$ donnée en  annexe 1  est la représentation graphique d'une fonction $f$ dérivable sur l'intervalle ]0 ; 1] qui respecte les trois conditions suivantes: \[(H):\: f(1) = 0\qquad f'(1) = 0,25\quad \text{et} \:\: \displaystyle\lim_{\substack{x \to 0\\x > 0}} f(x) = - \infty.\]

  1. La fonction $f$ peut-elle être une fonction polynôme du second degré ? Pourquoi ?
    2. Si une expression algébrique de $f$ est, sur l’intervalle $]0;1]$, $f(x)=ax^2+bx+c$ alors $\lim\limits_{x \to 0^+}=c$
    D’après l’énoncé on a $\lim\limits_{x\to 0^+}=-\infty$.
    La fonction $f$ ne donc pas une fonction polynôme du second degré.
    $\quad$
  2. Soit $g$ la fonction définie sur l'intervalle ]0 ; 1] par $g(x) = k \ln x$.
    1. Déterminer le réel $k$ pour que la fonction $g$ respecte les trois conditions $(H)$.
      2. La fonction $g$ est dérivable sur l’intervalle $]0;1]$ en tant que produit d’une fonction dérivable sur cet intervalle par un réel.
      Ainsi, pour tout réel $x\in]0;1]$ on a : $g'(x)=\dfrac{k}{x}$.
      Par conséquent $g'(1)=k$.
      Si la fonction $g$ vérifie les trois conditions (H) on a donc $g'(1)=0,25$ et donc $k=0,25$.
      Ainsi $g(x)=0,25\ln x$.
      De plus $g(1)=0,25\ln 1=0$
      Et, puisque $\lim\limits_{x \to 0^+} \ln x=-\infty$ et que $0,25>0$, on a$\lim\limits_{x \to 0^+}g(x)=-\infty$.
      $\quad$
    2. La courbe représentative de la fonction $g$ coïncide-t-elle avec la courbe $C$ ? Pourquoi ?
      3. On a $f(0,3)\approx -5,5$ et $g(0,3)\approx -0,30$.
      La courbe représentative de la fonction $g$ ne coïncide donc pas avec la courbe $C$.
      $\quad$
  3. Soit $h$ la fonction définie sur l'intervalle ]0 ; 1] par $h(x) = \dfrac{a}{x^4} + bx$ où $a$ et $b$ sont des réels. Déterminer $a$ et $b$ pour que la fonction $h$ respecte les trois conditions $(H)$.
    4. On a $h(1)=a+b=0 \iff a=-b$.
    La fonction $h$ est dérivable sur l’intervalle $]0;1]$ en tant que somme de fonctions dérivables sur cet intervalle.
    Ainsi, pour tout réel $x\in]0;1]$ on a $h'(x)=-\dfrac{4a}{x^5}+b$.
    Or $h'(1)=0,25 \iff -4a+b=0,25$.
    On doit donc résoudre le système :
    $\begin{align*} \begin{cases}a=-b\\-4a+b=0,25\end{cases} &\iff \begin{cases} a=-b\\4b+b=0,25\end{cases}\\
    &\iff \begin{cases} a=-b\\5b=0,25 \end{cases}\\
    &\iff \begin{cases} b=0,05\\a=-0,05\end{cases}\end{align*}$
    Ainsi $h(x)=0,05x-\dfrac{0,05}{x^4}$.
    Vérifions que les trois conditions sont bien vérifiées :
    $h(1)=0,05-0,05=0$.
    $h'(1)=0,05+\dfrac{4\times 0,05}{1^5}=0,25$.
    $\lim\limits_{x\to 0^+} h(x)=\lim\limits_{x\to 0^+}-\dfrac{0,05}{x^4}=-\infty$.
    $\quad$

 

Partie B


On admet dans cette partie que la courbe $C$ est la représentation graphique d'une fonction $f$continue, strictement croissante, définie et dérivable sur l'intervalle ]0 ; 1] d'expression: \[f(x) = \dfrac{1}{20}\left(x - \dfrac{1}{x^4} \right).\]

  1. Justifier que l'équation $f(x) = -5$ admet sur l'intervalle ]0 ; 1] une unique solution qui sera notée $\alpha$. Déterminer une valeur approchée de $\alpha$ à $10^{-2}$ près.
    2. On a $f(x)=\dfrac{1}{20}\left(x-\dfrac{1}{x^4}\right)$ sur l’intervalle $]0;1]$.
    Ainsi $f'(x)=\dfrac{1}{20}\left(1+\dfrac{4}{x^5}\right)$.
    Par conséquent, $f'(x)>0$ sur l’intervalle $]0;1]$ en tant que somme de fonctions positives sur cet intervalle.
    La fonction $f$ est donc continue et strictement croissante sur l’intervalle $]0;1]$.
    $\lim\limits_{x \to 0^+} f(x)=-\infty$ et $f(1)=0$.
    Or $-5\in]-\infty;0]$.
    D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation $f(x)=-5$ possède une unique solution $\alpha$ sur l’intervalle $]0;1]$.
    D’après la calculatrice $\alpha\approx 0,32$.
    $\quad$
  2. On admet que le volume d'eau en cm$^3$, contenu dans les 5 premiers centimètres de l'écoulement, est donné par la formule : $$V = \displaystyle\int_{\alpha}^1\pi x^2 f'(x)\:\text{d}x.$$
    1. Soit $u$ la fonction dérivable sur ]0 ; 1] définie par $u(x) = \dfrac{1}{2x^2}$. Déterminer sa fonction dérivée.
      2. Sur l’intervalle $]0;1]$ on a $u'(x)=\dfrac{1}{2}\times \dfrac{-2}{x^3}=-\dfrac{1}{x^3}$.
      $\quad$
    2. Déterminer la valeur exacte de $V$. En utilisant la valeur approchée de $\alpha$ obtenue à la question 1, donner alors une valeur approchée de $V$.
      3. On a :
      $\begin{align*} \displaystyle V&=\int_{\alpha}^1 \pi x^2 f'(x)\text{d} x \\
      &=\pi \int_{\alpha}^1 \left(\dfrac{1}{20}\left(1+\dfrac{4}{x^5}\right)\right)\times x^2\text{d} x \\
      &=\dfrac{\pi}{20}\int_{\alpha}^1 \left(x^2+\dfrac{4}{x^3}\right)\text{d} x \\
      &=\dfrac{\pi}{20}\left[\dfrac{x^3}{3}-4\times \dfrac{1}{2x^2}\right]_{\alpha}^1 \\
      &=\dfrac{\pi}{20}\left(\dfrac{1}{3}-2-\left(\dfrac{\alpha^3}{3}-\dfrac{2}{\alpha^2}\right)\right) \\
      &=\dfrac{\pi}{20}\left(-\dfrac{5}{3}-\dfrac{\alpha^3}{3}+\dfrac{2}{\alpha^2}\right)\\
      &\approx 2,8 \text{ cm}^3\end{align*}$.
      $\quad$
 Annexe 1
Courbe Ex1

Exercice 3 5 points


Suites et calcul intégral


On considère la suite $\left(I_n\right)$ définie par $I_0 = \displaystyle\int_0^{\frac{1}{2}}\dfrac{1}{1 - x}\:\text{d }x$ et pour tout entier naturel $n$ non nul \[I_n = \displaystyle\int_0^{\frac{1}{2}}\dfrac{x^n}{1 - x}\:\text{d }x.\]

  1. Montrer que $I_0 = \ln (2)$.
    1. Calculer $I_0 - I_1$.
    2. En déduire $I_1$.
    1. Montrer que, pour tout entier naturel $n,\: I_n - I_{n+1} = \dfrac{\left(\frac{1}{2} \right)^{n+1}}{n+1}$.
    2. Proposer un algorithme permettant de déterminer, pour un entier naturel $n$ donné, la valeur de $I_n$.
  4. Soit $n$ un entier naturel non nul. On admet que si $x$ appartient à l'intervalle $\left[0 ; \frac{1}{2}\right]$ alors $0 \leqslant \dfrac{x^n}{1 - x} \leqslant \dfrac{1}{2^{n-1}}$.
    1. Montrer que pour tout entier naturel $n$ non nul, $0 \leqslant I_n \leqslant \dfrac{1}{2^n}$.
    2. En déduire la limite de la suite $\left(I_n\right)$ lorsque $n$ tend vers $+\infty$.
  5. Pour tout entier naturel $n$ non nul, on pose \[S_n = \dfrac{1}{2} + \dfrac{\left(\frac{1}{2} \right)^2}{2} + \dfrac{\left(\frac{1}{2} \right)^3}{3} + \ldots +\dfrac{\left( \frac{1}{2}\right)^n}{n}. \]
    1. Montrer que pour tout entier naturel $n$ non nul, $S_n = 10 - I_n$.
    2. Déterminer la limite de $S_n$ lorsque $n$ tend vers $+\infty$.

 


Correction de l'exercice 3 (5 points)


Commun à tous les candidats

Suites et calcul intégral


On considère la suite $\left(I_n\right)$ définie par $I_0 = \displaystyle\int_0^{\frac{1}{2}}\dfrac{1}{1 - x}\:\text{d }x$ et pour tout entier naturel $n$ non nul \[I_n = \displaystyle\int_0^{\frac{1}{2}}\dfrac{x^n}{1 - x}\:\text{d }x.\]

  1. Montrer que $I_0 = \ln (2)$.
    2. On a :
    $\begin{align*} I_0&=\int_0^{1/2}\dfrac{1}{1-x}\text{d} x \\
    &=\left[-\ln(1-x)\right]_0^{1/2} \\
    &=-\ln(0,5)+\ln(1)\\
    &=\ln(2)\end{align*}$
    $\quad$
    1. Calculer $I_0 - I_1$.
      2. On a :
      $\begin{align*} I_0-I_1&=\displaystyle\int_0^{1/2}\dfrac{1}{1-x}\text{d} x-\int_0^{1/2}\dfrac{x}{1-x}\text{d} x \\
      &=\int_0^{1/2}\dfrac{1-x}{1-x}\text{d} x \\
      &=\int_0^{1/2}1\text{d} x \\
      &=\big[x\big]_0^{1/2}\\
      &=\dfrac{1}{2}\end{align*}$
      $\quad$
    2. En déduire $I_1$.
      3. Donc $\ln(2)-I_1=\dfrac{1}{2}\iff I_1=\ln(2)-\dfrac{1}{2}$.
      $\quad$
    1. Montrer que, pour tout entier naturel $n,\: I_n - I_{n+1} = \dfrac{\left(\frac{1}{2} \right)^{n+1}}{n+1}$.
      2. Pour tout entier naturel $n$ on a :
      $\begin{align*} I_n-I_{n+1}&=\displaystyle \int_0^{1/2}\dfrac{x^n}{1-x}\text{d} x-\int_0^{1/2}\dfrac{x^{n+1}}{1-x}\text{d} x \\
      &=\int_0^{1/2}\dfrac{x^n-x^{n+1}}{1-x}\text{d} x \\
      &=\int_0^{1/2}\dfrac{x^n(1-x)}{1-x}\text{d} x \\
      &=\int_0^{1/2}x^n\text{d} x \\
      &=\left[\dfrac{x^{n+1}}{n+1}\right]_0^{1/2}\\
      &=\dfrac{\left(\dfrac{1}{2}\right)^{n+1}}{n+1} \end{align*}$
      $\quad$
    2. Proposer un algorithme permettant de déterminer, pour un entier naturel $n$ donné, la valeur de $I_n$.
      3. On a donc, pour tout entier naturel $n$, $I_{n+1}=I_n-\dfrac{\left(\dfrac{1}{2}\right)^{n+1}}{n+1} $.
      On peut donc utiliser l’algorithme suivant :
      $$\begin{array}{|l|} \hline I\leftarrow \ln(2)\\ \text{Si }n>0 \\ \hspace{1cm} \text{Pour } k \text{ allant de 0 à } n-1 \text{faire}\\ \hspace{2cm} I\leftarrow I-\dfrac{\left(\dfrac{1}{2}\right)^{k+1}}{k+1} \\ \hspace{1cm} \text{Fin Pour}\\ \text{Fin Si}\\ \hline \end{array}$$
      $\quad$
  4. Soit $n$ un entier naturel non nul. On admet que si $x$ appartient à l'intervalle $\left[0 ; \frac{1}{2}\right]$ alors $0 \leqslant \dfrac{x^n}{1 - x} \leqslant \dfrac{1}{2^{n-1}}$.
    1. Montrer que pour tout entier naturel $n$ non nul, $0 \leqslant I_n \leqslant \dfrac{1}{2^n}$.
      2. On considère un entier naturel $n$ non nul.
      Sur l’intervalle $\left[0;\dfrac{1}{2}\right]$ on a $0\leq \dfrac{x^n}{1-x}\leq \dfrac{1}{2^{n-1}}$.
      En intégrant cette inégalité sur l’intervalle $\left[0;\dfrac{1}{2}\right]$ on obtient :
      $0\leq \displaystyle \int_0^{1/2} \dfrac{x^n}{1-x}\text{d} x \\\int_0^{1/2}\dfrac{1}{2^{n-1}}\text{d} x$
      Or $\displaystyle \int_0^{1/2}\dfrac{1}{2^{n-1}}\text{d} x=\dfrac{1}{2^{n-1}}\big[x\big]_0^{1/2}=\dfrac{1}{2^{n-1}}\times \dfrac{1}{2}=\dfrac{1}{2^{n}}$
      Donc $0\leq I_n\leq \dfrac{1}{2^{n}}$.
      $\quad$
    2. En déduire la limite de la suite $\left(I_n\right)$ lorsque $n$ tend vers $+\infty$.
      3. On a $-1<\dfrac{1}{2}<1$ donc $\lim\limits_{n\to +\infty}\dfrac{1}{2^n}= \lim\limits_{n\to +\infty} \left(\dfrac{1}{2}\right)^n=0$.
      D’après le théorème des gendarmes on a donc $\lim\limits_{n\to +\infty} I_n=0$.
      $\quad$
  5. Pour tout entier naturel $n$ non nul, on pose \[S_n = \dfrac{1}{2} + \dfrac{\left(\frac{1}{2} \right)^2}{2} + \dfrac{\left(\frac{1}{2} \right)^3}{3} + \ldots +\dfrac{\left( \frac{1}{2}\right)^n}{n}. \]
    1. Montrer que pour tout entier naturel $n$ non nul, $S_n = 10 - I_n$.
      2. Montrons par récurrence sur $n$, entier naturel non nul, que $S_n=I_0-I_n$.
      Initialisation : Si $n=1$ alors $I_0-I_1=\dfrac{1}{2}=S_1$.
      La propriété est vraie au rang $1$.
      $\quad$
      Hérédité : Supposons la propriété vraie au rang $n$. On a donc $S_n=I_0-I_n$.
      Montrons que la propriété est encore vraie au rang $n+1$, c’est-à-dire que $S_{n+1}=I_0-I_{n+1}$.
      $\begin{align*} S_{n+1}&=S_n+\dfrac{\left(\dfrac{1}{2}\right)^{n+1}}{n+1} \\
      &=I_0-I_n+\dfrac{\left(\dfrac{1}{2}\right)^{n+1}}{n+1}\\
      &=I_0-\left(I_n-\dfrac{\left(\dfrac{1}{2}\right)^{n+1}}{n+1}\right) \\
      &=I_0-I_{n+1}\end{align*}$
      La propriété est donc vraie au rang $n+1$.
      $\quad$
      Conclusion : La propriété est vraie au rang $1$ et est héréditaire.
      Par conséquent, pour tout entier naturel $n$, on a $S_n=I_0-I_n$.
      $\quad$
    2. Déterminer la limite de $S_n$ lorsque $n$ tend vers $+\infty$.
      3. On sait que $\lim\limits_{n\to +\infty}I_n=0$.
      Donc $\lim\limits_{n\to +\infty}S_n=I_0=\ln(2)$.
      $\quad$

Exercice 4 5 points


Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques


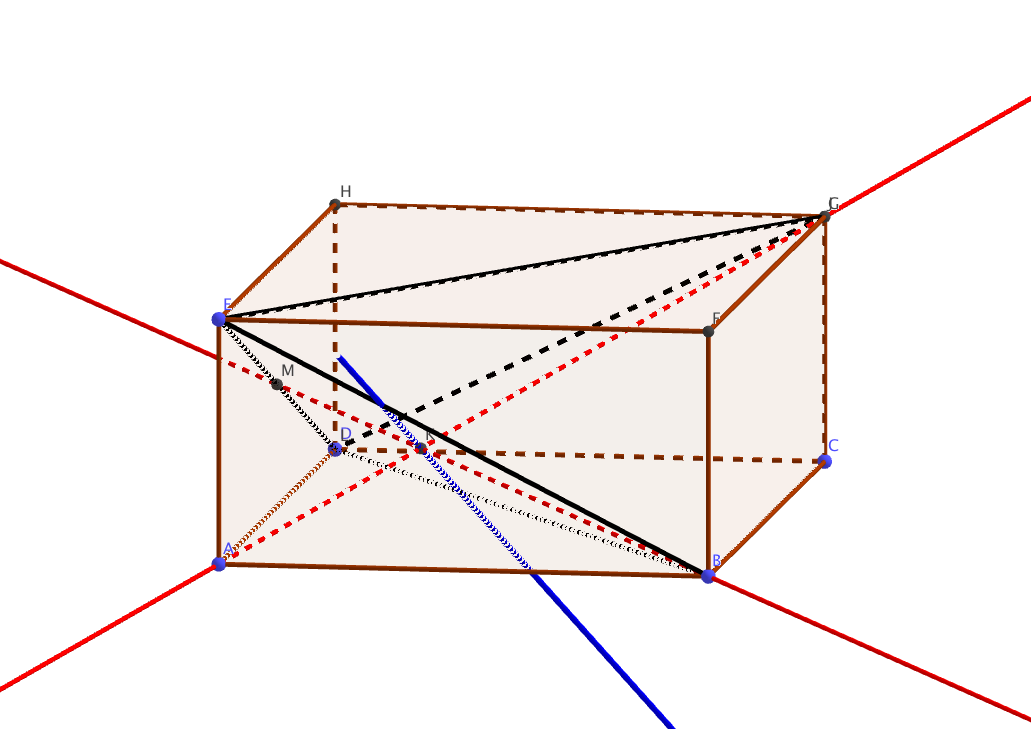
Sur la figure donnée en annexe 2 à rendre avec la copie :

  • ABCDEFGH est un parallélépipède rectangle tel que AB $= 12$, AD $= 18$ et AE $= 6$
  • EBDG est un tétraèdre.


 L'espace est rapporté à un repère orthonormal d'origine A dans lequel les points B, D et E ont pour coordonnées respectives B(12 ; 0 ; 0), D(0 ; 18 ; 0) et E(0 ; 0 ; 6).

  1. Démontrer que le plan (EBD) a pour équation cartésienne $3x + 2y + 6z - 36 = 0$.
    1. Déterminer une représentation paramétrique de la droite (AG).
    2. En déduire que la droite (AG) coupe le plan (EBD) en un point K de coordonnées (4 ; 6 ; 2) .
  3. La droite (AG) est-elle orthogonale au plan (EBD) ? Justifier.
    1. Soit M le milieu du segment [ED]. Démontrer que les points B, K et M sont alignés.
    2. Construire alors le point K sur la figure donnée en annexe 2 à rendre avec la copie.
  5. On note P le plan parallèle au plan (ADE) passant par le point K.
    1. Démontrer que le plan P coupe le plan (EBD) selon une parallèle à la droite (ED).
    2. Construire alors sur l'annexe 2 à rendre avec la copie l'intersection du plan P et de la face EBD du tétraèdre EBDG.

       ANNEXE 2
      pave

 


Correction de l'exercice 4 5 points


Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques


Sur la figure donnée en annexe 2 à rendre avec la copie :

  • ABCDEFGH est un parallélépipède rectangle tel que AB $= 12$, AD $= 18$ et AE $= 6$
  • EBDG est un tétraèdre.


 L'espace est rapporté à un repère orthonormal d'origine A dans lequel les points B, D et E ont pour coordonnées respectives B(12 ; 0 ; 0), D(0 ; 18 ; 0) et E(0 ; 0 ; 6).

  1. Démontrer que le plan (EBD) a pour équation cartésienne $3x + 2y + 6z - 36 = 0$.
    2. Montrons que les coordonnées des points $E, B$ et $D$ sont solutions de l’équation fournie.
    Pour le point $E$ : $3\times 0+2\times 0+6\times 6-36=36-36=0$.
    Pour le point $B$ : $3\times 12+2\times 0+6\times 0-36=36-36=0$.
    Pour le point $D$ : $3\times 0+2\times 18+6\times 0-36=36-36=0$.
    Une équation cartésienne du plan $(EBD)$ est donc $3x+2y+6z-36=0$.
    $\quad$
    1. Déterminer une représentation paramétrique de la droite (AG).
      2. On a $\vec{AG}(12;18;6)$.
      Ainsi une représentation paramétrique de la droite $(AG)$ est : $$\begin{cases} x=12t\\y=18t\\z=6t\end{cases} \quad, t\in\matbb R$$
      $\quad$
    2. En déduire que la droite (AG) coupe le plan (EBD) en un point K de coordonnées (4 ; 6 ; 2) .
      3. Prenons $t=\dfrac{1}{3}$. On a alors $\begin{cases} 12t=4\\18t=6\\6t=3\end{cases}$. Le point $K(4;6;3)$ appartient donc à la droite $(AG)$.
      De plus $3\times 4+2\times 6+6\times 2-36=12+12+12-36=0$.
      Le point $K$ appartient également au plan $(EBD)$.
      Un vecteur normal au plan $(EBD)$ est $\vec{n}(3;2;6)$
      $\vec{n}.\vec{AG}=3\times 12+2\times 18+6\times 6=108\neq 0$. La droite $(AG)$ n’est donc pas incluse dans le plan $(EBD)$.
      Ainsi la droite $(AG)$ coupe le plan $(EBD)$ en un point $K$ de coordonnées $(4;6;2)$.
      $\quad$
  3. La droite (AG) est-elle orthogonale au plan (EBD) ? Justifier.
    4. On a $\vec{AG}(12;18;6)$ et $\vec{n}(3;2;6)$.
    Ils ont la même troisième coordonnée mais les deux autres sont différentes. Ces deux vecteurs ne sont donc pas colinéaires et la droite $(AG)$ n’est pas orthogonale au plan $(EBD)$.
    $\quad$
    1. Soit M le milieu du segment [ED]. Démontrer que les points B, K et M sont alignés.
      2. Le point $M$ est le milieu du segment $[ED]$.
      Ainsi $x_M=\dfrac{0+0}{2}$, $y_M=\dfrac{18+0}{2}=9$ et $z_M=\dfrac{0+6}{2}=3$.
      Les coordonnées du points $M$ sont donc $(0;9;3)$.
      Par conséquent :
      – les coordonnées du vecteur sont $\vec{BM}(-12;9;3)$;
      – les coordonnées du vecteur sont $\vec{BK}(-8;6;2)$.
      $\dfrac{-12}{-8}=1,5$, $\dfrac{9}{6}=1,5$ et $\dfrac{3}{2}=1,5$.
      Cela signifie donc que $\vec{BM}=1,5\vec{BK}$.
      Les deux vecteurs sont colinéaires et les points $B$, $M$ et $K$ sont alignés.
      $\quad$
    2. Construire alors le point K sur la figure donnée en annexe 2 à rendre avec la copie.
      3. Le point $K$ est donc le point d’intersection des droites $(AG)$ et $(BM)$.
      $\quad$
  5. On note P le plan parallèle au plan (ADE) passant par le point K.
    1. Démontrer que le plan P coupe le plan (EBD) selon une parallèle à la droite (ED).
      2. Les plans $(AED)$ et $(EBD)$ se coupent selon la droite $(ED)$.
      Le plan $P$ est parallèle au plan $(AED)$ et passe par le point $K$.
      Le point $K$ appartient donc aux plans $(EBD)$ et $P$.
      Par conséquent l’intersection du plan $P$ et du plan $(EBD)$ est une droite parallèle à la droite $(ED)$ passant par le point $K$.
      $\quad$
    2. Construire alors sur l'annexe 2 à rendre avec la copie l'intersection du plan P et de la face EBD du tétraèdre EBDG.

      3.  ANNEXE 2
      pavesol
      L’intersection du plan $P$ et de la face $EBD$ est représentée en bleue.

Spécialité 5 points


Candidats AYANT SUIVI l'enseignement de spécialité mathématiques


On considère la matrice $M = \begin{pmatrix}2&3\\1&2\end{pmatrix}$ et les suites d'entiers naturels $\left(u_n\right)$ et $\left(v_n\right)$ définies par: $u_0 = l,\: v_0 = 0$, et pour tout entier naturel $n$, $\begin{pmatrix}u_{n+1}\\v_{n+1}\end{pmatrix} = M\begin{pmatrix}u_{n}\\v_{n}\end{pmatrix}$.
Les deux parties peuvent être traitées de façon indépendante.

Partie A


On a calculé les premiers termes de la suite $\left(v_n\right)$ : $$ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline n &0 &1 &2 &3 &4&5 &6&7&8&9&10&11&12\\ \hline v_n&0 &1 &4 &15 &56 &209&780& 2911 & 10864 & 40545 & 151316 & 564719 & 2107560 \\ \hline \end{array} $$

  1. Conjecturer les valeurs possibles du chiffre des unités des termes de la suite $\left(v_n\right)$.
  2. On admet que pour tout entier naturel $n, \:\begin{pmatrix}u_{n+3}\\v_{n+3}\end{pmatrix} = M^3\begin{pmatrix}u_{n}\\v_{n}\end{pmatrix}$.
    1. Justifier que pour tout entier nature $n,\:\left\{\begin{array}{l c l} u_{n+3}&=&26u_n + 45v_n\\ v_{n+3}&=&15u_n + 26v_n \end{array}\right.$.
    2. En déduire que pour tout entier naturel $n :\: v_{n+3} \equiv v_n \:[5]$.
  3. Soit $r$ un entier naturel fixé. Démontrer, à l'aide d'un raisonnement par récurrence, que, pour tout entier naturel $q,\: v_{3q+r} \equiv v_r \:[5]$.
  4. En déduire que pour tout entier naturel $n$ le terme $v_n$ est congru à 0, à 1 ou à 4 modulo 5.
  5. Conclure quant à l'ensemble des valeurs prises par le chiffre des unités des termes de la suite $\left(v_n\right)$·

 

Partie B


L'objectif de cette partie est de démontrer que $\sqrt{3}$ n'est pas un nombre rationnel en utilisant la matrice $M$.
Pour cela, on effectue un raisonnement par l'absurde et on suppose que $\sqrt{3}$ est un nombre rationnel. Dans ce cas, $\sqrt{3}$ peut s'écrire sous la forme d'une fraction irréductible $\dfrac{p}{q}$ où $p$ et $q$ sont des entiers naturels non nuls, avec $q$ le plus petit entier naturel possible.

  1. Montrer que $q < p < 2q$.
  2. On admet que la matrice $M$ est inversible. Donner son inverse $M^{-1}$ (aucune justification n'est attendue). Soit le couple $(p' ; q')$ défini par $\begin{pmatrix}p'\\q'\end{pmatrix} = M^{-1}\begin{pmatrix}p\\q\end{pmatrix}$.
    1. Vérifier que $p' = 2p - 3q$ et que $q' = -p + 2q.$
    2. Justifier que $(p' ; q')$ est un couple d'entiers relatifs.
    3. On rappelle que $p = q\sqrt{3}$. Montrer que $p' = q'\sqrt{3}$.
    4. Montrer que $0 < q' < q$.
    5. En déduire que $\sqrt{3}$ n'est pas un rationnel.

 


Correction de l'exercice de Spécialité 5 points


Candidats AYANT SUIVI l'enseignement de spécialité mathématiques


On considère la matrice $M = \begin{pmatrix}2&3\\1&2\end{pmatrix}$ et les suites d'entiers naturels $\left(u_n\right)$ et $\left(v_n\right)$ définies par: $u_0 = l,\: v_0 = 0$, et pour tout entier naturel $n$, $\begin{pmatrix}u_{n+1}\\v_{n+1}\end{pmatrix} = M\begin{pmatrix}u_{n}\\v_{n}\end{pmatrix}$.
Les deux parties peuvent être traitées de façon indépendante.

Partie A


On a calculé les premiers termes de la suite $\left(v_n\right)$ : $$ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline n &0 &1 &2 &3 &4&5 &6&7&8&9&10&11&12\\ \hline v_n&0 &1 &4 &15 &56 &209&780& 2911 & 10864 & 40545 & 151316 & 564719 & 2107560 \\ \hline \end{array} $$

  1. Conjecturer les valeurs possibles du chiffre des unités des termes de la suite $\left(v_n\right)$.
    2. Il semblerait que les valeurs possibles du chiffre des unités des termes de la suite $\left(v_n\right)$ soit $0$, $1$, $4$, $5$, $6$ et $9$.
    $\quad$
  2. On admet que pour tout entier naturel $n, \:\begin{pmatrix}u_{n+3}\\v_{n+3}\end{pmatrix} = M^3\begin{pmatrix}u_{n}\\v_{n}\end{pmatrix}$.
    1. Justifier que pour tout entier nature $n,\:\left\{\begin{array}{l c l} u_{n+3}&=&26u_n + 45v_n\\ v_{n+3}&=&15u_n + 26v_n \end{array}\right.$.
      2. D’après la calculatrice on a $M^3=\begin{pmatrix}26&45\\15&26\end{pmatrix}$.
      Pour tout entier naturel $n$ on a donc :
      $\begin{pmatrix}u_{n+3}\\v_{n+3}\end{pmatrix}=\begin{pmatrix}26&45\\15&26\end{pmatrix}\times \begin{pmatrix}u_{n}\\v_{n}\end{pmatrix}$
      Par conséquent $\begin{cases} u_{n+3}=26u_n+45v_n\\v_{n+3}=15u_n+26v_n\end{cases}$.
      $\quad$
    2. En déduire que pour tout entier naturel $n :\: v_{n+3} \equiv v_n \:[5]$.
      3. Pour tout entier naturel $n$ on a donc : $v_{n+3}\equiv 26v_n~[5]$ soit $v_{n+3}\equiv v_n~[5]$.
      $\quad$
  3. Soit $r$ un entier naturel fixé. Démontrer, à l'aide d'un raisonnement par récurrence, que, pour tout entier naturel $q,\: v_{3q+r} \equiv v_r \:[5]$.
    4. Soit $r$ un entier naturel fixé.
    Montrons par récurrence sur l’entier naturel $q$ que $v_{3q+r}\equiv v_r~[5]$.
    Initialisation : Si $q=0$ alors $v_{3q+r}=v_r\equiv v_r~[5]$.
    La propriété est vraie au rang $1$.
    $\quad$
    Hérédité : On suppose la propriété vraie au rang $q$. Donc $v_{3q+r}\equiv v_r~[5]$.
    Montrons qu’elle encore vraie au rang $q+1$, c’est-à-dire que $v_{3(q+1)+r}\equiv v_r~[5]$ soit encore $v_{3q+r+3}\equiv v_r~[5]$.
    D’après la question précédente, en prenant $n=3q+r$, on a $v_{3q+r+3}\equiv v_{3q+r}~[5]$.
    D’après l’hypothèse de récurrence on a $v_{3q+r}\equiv v_r~[5]$.
    Par conséquent $v_{3(q+1)+r}\equiv v_r~[5]$
    La propriété est vraie au rang $q+1$.
    $\quad$
    Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
    Par conséquent, pour tout entier naturel $q$ on a $v_{3q+r}\equiv v_r~[5]$.
    $\quad$
  4. En déduire que pour tout entier naturel $n$ le terme $v_n$ est congru à 0, à 1 ou à 4 modulo 5.
    5. Ainsi, pour tout entier naturel $q$ on a :
    – $v_{3q}\equiv v_0~[5]$ soit $v_{3q}\equiv 0~[5]$
    – $v_{3q+1}\equiv v_1~[5]$ soit $v_{3q+1}\equiv 1~[5]$
    – $v_{3q+2}\equiv v_2~[5]$ soit $v_{3q+2}\equiv 4~[5]$
    On a ainsi parcouru tous les termes de la suite $\left(v_n\right)$.
    Pour tout entier naturel $n$, le terme $v_n$ est donc congru à $0$, $1$ ou $4$ modulo $5$.
    $\quad$
  5. Conclure quant à l'ensemble des valeurs prises par le chiffre des unités des termes de la suite $\left(v_n\right)$·
    6. Pour tout entier naturel $n$, il existe un entier naturel $k$ tel que $v_n=0+5k$, $v_n=1+5k$ ou $v_n=4+5k$.
    – Si $k$ est pair il s’écrit alors sous la forme $k=2p$ et on a donc :
    $v_n=0+10p$, $v_n=1+10p$ ou $v_n=4+10p$ ce qui signifie que $v_n$ est congru à $0$, $1$ ou $4$.
    – Si $k$ est impair il s’écrit alors sous la forme $k=2p+1$ et on a donc :
    $v_n=0+10p+5$, $v_n=1+10p+5$ ou $v_n=4+10p+5$ ce qui signifie que $v_n$ est congru à $5$, $6$ ou $9$.
    L’ensemble des valeurs prises par le chiffre des unités des termes de la suite $\left(v_n\right)$ est donc $\left\{0;1;4;5;6;9\right\}$.
    $\quad$

 

Partie B


L'objectif de cette partie est de démontrer que $\sqrt{3}$ n'est pas un nombre rationnel en utilisant la matrice $M$.
Pour cela, on effectue un raisonnement par l'absurde et on suppose que $\sqrt{3}$ est un nombre rationnel. Dans ce cas, $\sqrt{3}$ peut s'écrire sous la forme d'une fraction irréductible $\dfrac{p}{q}$ où $p$ et $q$ sont des entiers naturels non nuls, avec $q$ le plus petit entier naturel possible.

  1. Montrer que $q < p < 2q$.
    2. On a donc $\sqrt{3}=\dfrac{p}{q}$.
    Puisque $\sqrt{3}>1$, cela signifie que $p>q$.
    $\sqrt{3}=\dfrac{p}{q} \ssi p=q\sqrt{3}$ et donc $p^2=3q^2<4q^2$.
    Comme $p$ et $q$ sont des entiers naturels non nuls on a donc $p<2q$.
    Ainsi $q<p<2q$.
    $\quad$
  2. On admet que la matrice $M$ est inversible. Donner son inverse $M^{-1}$ (aucune justification n'est attendue). Soit le couple $(p' ; q')$ défini par $\begin{pmatrix}p'\\q'\end{pmatrix} = M^{-1}\begin{pmatrix}p\\q\end{pmatrix}$.
    3. On a $M^{-1}=\begin{pmatrix}2&-3\\-1&2\end{pmatrix}$
    $\quad$
    $\quad$
    1. Vérifier que $p' = 2p - 3q$ et que $q' = -p + 2q.$
      2. On a :
      $\begin{align*} \begin{pmatrix} p’\\q’\end{pmatrix}=\begin{pmatrix} 2&-3\\-1&2\end{pmatrix}\times \begin{pmatrix}p\\q\end{pmatrix} &\ssi \begin{pmatrix}p’\\q’\end{pmatrix}=\begin{pmatrix}2p-3q\\-p+2q\end{pmatrix} \\
      &\ssi \begin{cases} p’=2p-3q\\q’=-p+2q\end{cases}\end{align*}$
      $\quad$
    2. Justifier que $(p' ; q')$ est un couple d'entiers relatifs.
      3. $p$ et $q$ sont des entiers naturels donc $2p-3q$ et $-p+2q$ sont des entiers.
      On sait que $q<p<2q$
      Donc $2q-3q<2p-3q<4q-3q \ssi -q<p'<q$ : ce qui signifie que $p’\in \Z$.
      De même $-2q<-p<-q \ssi 0<-p+2q<q$ : ce qui signifie que $q’\in \N$ et donc $q’\in \Z$.
      $(p’,q’)$ est par conséquent un couple d’entier relatifs.
      $\quad$
    3. On rappelle que $p = q\sqrt{3}$. Montrer que $p' = q'\sqrt{3}$.
      4. On a $q’=-p+2q=-q\sqrt{3}+2q=\left(2-\sqrt{3}\right)q$.
      Donc
      $\begin{align*}q&=\dfrac{q’}{2-\sqrt{3}}\\
      &=\dfrac{q’}{2-\sqrt{3}}\times \dfrac{2+\sqrt{3}}{2+\sqrt{3}}\\
      &=\left(2+\sqrt{3}\right)q’\end{align*}$.
      De plus :
      $\begin{align*} p’&=2p-3q\\
      &=2q\sqrt{3}-3q\\
      &=\left(2\sqrt{3}-3\right)q\\
      &=\left(2\sqrt{3}-3\right)\times \left(2+\sqrt{3}\right)q’\\
      &=q’\sqrt{3}\end{align*}$
      $\quad$
    4. Montrer que $0 < q' < q$.
      5. On a montré à la question 3.b. que $q’>0$.
      D’après la question précédente on a $q=\left(2+\sqrt{3}\right)q’$.
      Or $2+\sqrt{3}>2>1$ donc $q>q’$.
      Par conséquent $0<q'<q$.
      $\quad$
    5. En déduire que $\sqrt{3}$ n'est pas un rationnel.
      6. On a donc montrer qu’on pouvait écrire $\sqrt{3}=\dfrac{p’}{q’}$ où $p$ et $q$ sont des entiers relatifs.
      De plus $0<q'<q$. Cela signifie donc, puisque $q’$ et $\sqrt{3}$ sont positifs que $p’$ l’est aussi.
      Or $q$ le plus petit entier naturel tel que $\sqrt{3}$ s’écrive sous la forme $\dfrac{p}{q}$.
      Il y a donc une absurdité et $\sqrt{3}$ n’est pas un rationnel.
      $\quad$
  • Vues: 36525

Les plus lus

Les news

Rechercher