Baccalauréat S Asie 21 juin 2018 - Correction Exercice 4

Page 8 sur 10: Correction Exercice 4

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Dans cet exercice, $x$ et $y$ sont des nombres réels supérieurs à 1.
Dans le plan complexe muni d'un repère orthonormé direct $\left(\text{O}~;~\vec{u},~\vec{v}\right)$, on considère les points A, B et C d'affixes respectives \[z_{\text{A}} = 1 + \text{i}, \: z_{\text{B}} = x + \text{i}\: \text{ et }\: z_{\text{C}} = y + \text{i}.\]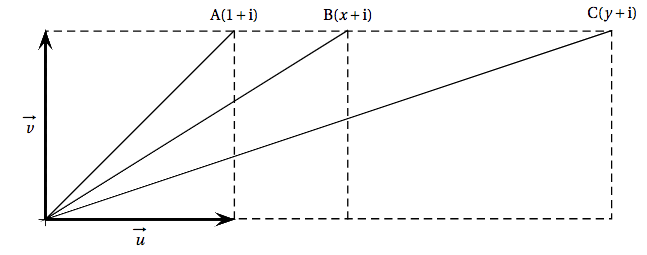


Problème : on cherche les valeurs éventuelles des réels $x$ et $y$, supérieures à 1, pour lesquelles : \[ \text{OC} = \text{OA} \times \text{OB} \quad \text{et}\: \left(\vec{u},~\vec{\text{OB}}\right) + \left(\vec{u},~\vec{\text{OC}}\right) = \left(\vec{u},~\vec{\text{OA}}\right).\]

1. Démontrer que si $\text{OC} = \text{OA} \times \text{OB}$, alors $y^2 = 2x^2 + 1$.
On a $OC=|y+\text{i}|=\sqrt{y^2+1}$, $OA=|1+\text{i}|=\sqrt{2}$ et $OB=|x+\text{i}|=\sqrt{x^2+1}$.
Ainsi :
$OC=OA\times OB \iff \sqrt{y^2+1}=\sqrt{2}\sqrt{x^2+1}$
Par conséquent $ y^2+1=2x^2+2$ soit $y^2=2x^2+1$
$\quad$
2. Reproduire sur la copie et compléter l'algorithme ci-après pour qu'il affiche tous les couples $(x,~y)$ tels que : \[\left\{\begin{array}{l} y^2 = 2x^2 + 1 \\ x \text{ et } y \text{ sont des nombres entiers } \\ 1 \leqslant x \leqslant 10 \text{ et } 1 \leqslant y \leqslant 10 \\ \end{array}\right.\] $$\begin{array}{ |l|}\hline \text{ Pour } x \text{ allant de 1 à } \ldots \text{ faire }\\ \hspace{0.5cm} \text{ Pour } \ldots\\ \hspace{1cm} \text{ Si }\ldots\\ \hspace{1.5cm} \text{ Afficher } x \text{ et } y \\ \hspace{1cm} \text{Fin Si}\\ \hspace{0.5cm} \text{Fin Pour}\\ \text{Fin Pour}\\ \hline \end{array}$$ Lorsque l'on exécute cet algorithme, il affiche la valeur $2$ pour la variable $x$ et la valeur $3$ pour la variable $y$.
On obtient l’algorithme suivant :
$$\begin{array}{ |l|}\hline \text{ Pour } x \text{ allant de 1 à } 10 \text{ faire }\\ \hspace{0.5cm} \text{ Pour } y \text{ allant de 1 à } 10\\ \hspace{1cm} \text{ Si }y^2=2x^2+1\\ \hspace{1.5cm} \text{ Afficher } x \text{ et } y \\ \hspace{1cm} \text{Fin Si}\\ \hspace{0.5cm} \text{Fin Pour}\\ \text{Fin Pour}\\ \hline \end{array}$$
3. Étude d'un cas particulier : dans cette question seulement, on prend $x = 2$ et $y = 3$.
   1. Donner le module et un argument de $z_{\text{A}}$.
   On a $\left|z_A\right|=|1+\text{i}|=\sqrt{2}$
   Donc $z_A=\sqrt{2}\left(\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}\right)$ $= \sqrt{2}\left(\cos \left(\dfrac{\pi}{4}\right)+\text{i} \sin \left(\dfrac{\pi}{4}\right)\right)$.
   Un argument de $z_A$ est donc $\dfrac{\pi}{4}$.
   $\quad$
   
   2. Montrer que $\text{OC} = \text{OA} \times \text{OB}$.
   Si $x=2$ et $y=3$.
   Alors $OC=\sqrt{3^2+1}=\sqrt{10}$, $OA=\sqrt{2}$ et $\sqrt{OB}=\sqrt{2^2+1}=\sqrt{5}$
   Par conséquent $OA\times OB=\sqrt{2}\times \sqrt{5}=\sqrt{10} =OC$.
   $\quad$
   
   3. Montrer que $z_{\text{B}}z_{\text{C}} = 5 z_{\text{A}}$ et en déduire que $\left(\vec{u},~\vec{\text{OB}}\right) + \left(\vec{u},~\vec{\text{OC}}\right) = \left(\vec{u},~\vec{\text{OA}}\right)$.
   On a :
   $\begin{align*}z_Bz_C&=(2+\text{i})(3+\text{i})\\
   &=6+2\text{i}+3\text{i}-1\\
   &=5+5\text{i}\\
   &=5(1+\text{i})\\
   &=5z_A
   \end{align*}$
   Ainsi arg$\left(z_Bz_C\right)=$ arg$\left(z_B\right)+$arg$\left(z_C\right)$ $=\left(\vec{u},\vec{OB}\right)+\left(\vec{u},\vec{OC}\right)$.
   arg$\left(5z_A\right)$ $=$arg$\left(z_A\right)=\left(\vec{u},\vec{OA}\right)$.
   Donc $\left(\vec{u},\vec{OB}\right)+\left(\vec{u},\vec{OC}\right)=\left(\vec{u},\vec{OA}\right)$
   $\quad$
4. On revient au cas général, et on cherche s'il existe d'autres valeurs des réels $x$ et $y$ telles que les points A, B et C vérifient les deux conditions: $\text{OC} = \text{OA} \times \text{OB} \quad \text{et}\: \left(\vec{u},~\vec{\text{OB}}\right) + \left(\vec{u},~\vec{\text{OC}}\right) = \left(\vec{u},~\vec{\text{OA}}\right)$. On rappelle que si $\text{OC} = \text{OA} \times \text{OB}$, alors $y^2 = 2x^2 + 1$ (question 1.).
   1. Démontrer que si $\left(\vec{u},~\vec{\text{OB}}\right) + \left(\vec{u},~\vec{\text{OC}}\right) = \left(\vec{u},~\vec{\text{OA}}\right)$, alors arg$\left[\dfrac{(x + \text{i})(y + \text{i})}{1 + \text{i}}\right] = 0 \:\text{mod }\: 2\pi$. En déduire que sous cette condition : $x + y - xy + 1 = 0$.
   arg$\left(\dfrac{(x+\text{i})(y+\text{i})}{1+\text{i})}\right)$
   $=$ arg $\left((x+\text{i})(y+\text{i})\right)-$ arg$\left(1+\text{i}\right)$
   $=$ arg$\left(x+\text{i}\right)+$ arg$\left(y+\text{i}\right)-\left(\vec{u},\vec{OA}\right)$
   $=\left(\vec{u},\vec{OB}\right)+\left(\vec{u},\vec{OC}\right)-\left(\vec{u},\vec{OA}\right)$
   $=0$ mod $2\pi$
   $\quad$
   
   2. Démontrer que si les deux conditions sont vérifiées et que de plus $x \neq 1$, alors: \[y= \sqrt{2x^2 + 1}\quad \text{et} \: y = \dfrac{x + 1}{x - 1}.\]
   Si $OC=OA\times OB$ alors $y^2=2x^2+1$.
   Puisque $y>1$ on a $y=\sqrt{2x^2+1}$
   Si $\left(\vec{u},\vec{OB}\right)+\left(\vec{u},\vec{OC}\right)=\left(\vec{u},\vec{OA}\right)$ alors arg$\left(\dfrac{(x+\text{i})(y+\text{i})}{1+\text{i})}\right)=0$ mod $2\pi$
   Or
   $\begin{align*} \dfrac{(x+\text{i})(y+\text{i})}{1+\text{i}}&= \dfrac{(x+\text{i})(y+\text{i})}{1+\text{i}}\times \dfrac{1-\text{i}}{1-\text{i}} \\
   &=\dfrac{\left(xy+\text{i} x+\text{i} y-1\right)(1-\text{i})}{2} \\
   &=\dfrac{\left((xy-1)+\text{i}(x+y)\right)(1-\text{i})}{2}\\
   &=\dfrac{(xy-1+x+y)+\text{i}(x+y-xy+1)}{2}
   \end{align*}$
   Or arg$\left(\dfrac{(x+\text{i})(y+\text{i})}{1+\text{i})}\right)=0$ mod $2\pi$
   $\iff x+y-xy+1=0$
   $\iff y(1-x)=-1-x$
   $\iff y=\dfrac{x+1}{x-1}$ si $x\neq 1$
   $\quad$
5. On définit les fonctions $f$ et $g$ sur l'intervalle $]1~;~+ \infty[$ par : \[f(x) = \sqrt{2x^2 + 1}\quad \text{et} \: g(x) = \dfrac{x + 1}{x - 1}.\] Déterminer le nombre de solutions du problème initial. On pourra utiliser la fonction $h$ définie sur l'intervalle $]1~;~+ \infty[$ par $h(x) = f(x) - g(x)$ et s'appuyer sur la copie d'écran d'un logiciel de calcul formel donnée ci-dessous. $$\begin{array}{|c|}\hline f(x) := \text{sqrt}(2*x\verb+^+2+1) \\ \hline \hspace{1.5cm} x \to \sqrt{2*x^2+1} \\ \hline \text{deriver}(f) \\ \hline \hspace{1.5cm} x \to \dfrac{2*x}{\sqrt{2*x^2+ 1}} \\ \hline g(x) :=(x+1)/(x-1) \\ \hline \hspace{1.5cm} x \to \dfrac{x + 1}{x - 1} \\ \hline \text{deriver}(g) \\ \hline \hspace{1.5cm} x \to - \dfrac{2}{(x - 1)^2} \\ \hline \end{array}$$
La fonction $h$ est dérivable sur l’intervalle $]1;+\infty[$ comme somme de fonctions dérivables sur cet intervalle.
On a $h'(x)=\dfrac{2x}{\sqrt{2x^2+1}}+\dfrac{2}{(x-1)^2}$.
Puisque $x>1$ cela signifie donc que $h'(x)>0$.
La fonction $h$ est donc strictement croissante sur $]1;+\infty[$.
$\lim\limits_{x \to 1^+}f(x)=\sqrt{3}$
$\lim\limits_{x \to 1^+} x-1=0^+$ et $\lim\limits_{x \to 1^+}x+1=2$ donc $\lim\limits_{x \to 1^+} g(x)=+\infty$.
Par conséquent $\lim\limits_{x \to 1^+} h(x)=-\infty$
$\lim\limits_{x \to +\infty} 2x^2+1=+\infty$ et $\lim\limits_{X \to +\infty} \sqrt{X}=+\infty$ donc $\lim\limits_{x \to +\infty} f(x)=+\infty$
D’après la limite du quotient des termes de plus haut degré on a :
$\lim\limits_{x \to +\infty} h(x)=\lim\limits_{x \to +\infty} \dfrac{x}{x}=1$
Donc $\lim\limits_{x \to +\infty} h(x)=+\infty$
La fonction $h$ est continue (car dérivable) et strictement croissante sur l’intervalle $]1;+\infty[$.
D’après les calculs de limite précédent on est en mesure d’appliquer le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) et l’équation $h(x)=0$ possède une unique solution sur l’intervalle $]1;+\infty[$.
Le problème initial possède donc au plus une solution (il n’y avait pas d’équivalence dans ce qui a été montré dans les questions précédentes).
On a vu à la question 3. que $2$ était une solution du problème.
Le problème initial possède donc exactement une solution.
$\quad$