Baccalauréat S Asie 21 juin 2018 - Correction Exercice 3

Page 6 sur 10: Correction Exercice 3

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

On se place dans un repère orthonormé d'origine O et d'axes (O$x$), (O$y$) et (O$z$). Dans ce repère, on donne les points A$(- 3~;~0~;~0)$, B$(3~;~0~;~0)$ , C$\left(0~;~3\sqrt{3}~;~0\right)$ et D$\left(0~;~\sqrt{3}~;~2\sqrt{6}\right)$. On note H le milieu du segment [CD] et I le milieu du segment [BC].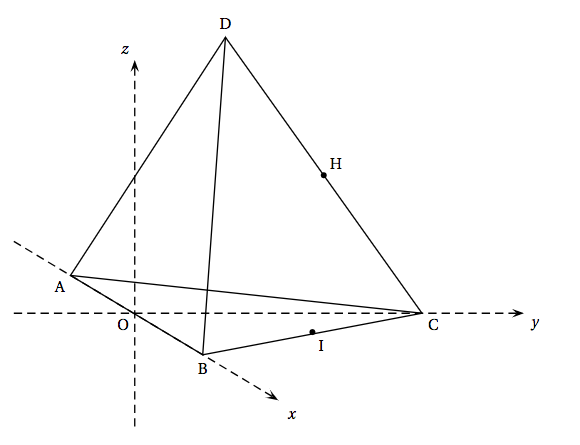 

 

1. Calculer les longueurs AB et AD.
$AB=\sqrt{\left(3-(-3)\right)^2+0^2+0^2}=\sqrt{36}=6$
$\begin{align*} AD&=\sqrt{3^2+3+4\times 6} \\
&=\sqrt{9+3+24}\\
&=\sqrt{36}\\
&=6
\end{align*}$
$\quad$


On admet pour la suite que toutes les arêtes du solide ABCD ont la même longueur, c'est-à-dire que le tétraèdre ABCD est un tétraèdre

2. Étude de la section du tétraèdre ABCD par le plan $\mathcal{P}$
   1. Montrer qu'une équation cartésienne du plan $\mathcal{P}$ est: $2y\sqrt{3} + z\sqrt{6} - 9 = 0$.
   $H$ est le milieu du segment $[CD]$ donc $H$ a pour coordonnées $\left(0;2\sqrt{3};\sqrt{6}\right)$.
   Par conséquent $\vec{OH}\left(0;2\sqrt{3};\sqrt{6}\right)$.
   Une équation cartésienne du plan $\mathcal{P}$ est de la forme $2\sqrt{3}y+\sqrt{6}z+d=0$.
   $I$ est le milieu du segment $[BC]$ donc ses coordonnées sont $\left(1,5;1,5\sqrt{3};0\right)$.
   Il appartient au plan $\mathcal{P}$.
   Par conséquent $2\sqrt{3}\times 1,5\sqrt{3}+\sqrt{6}\times 0+d=0 \iff 9+d=0 \iff d=-9$
   Une équation cartésienne du plan $\mathcal{P}$ est donc $$2y\sqrt{3}+z\sqrt{6}-9=0$$
   $\quad$
   
   2. Démontrer que le milieu J de [BD] est le point d'intersection de la droite (BD) et du plan $\mathcal{P}$.
   $J$ est le milieu de $[BD]$. Ses coordonnées sont donc $\left(1,5;0,5\sqrt{3};\sqrt{6}\right)$.
   Regardons si ses coordonnées vérifient l’équation cartésienne du plan $\mathcal{P}$.
   $2\sqrt{3}\times 0,5\sqrt{3}+\sqrt{6}\times \sqrt{6}-9=3+6-9=0$.
   Donc $J$ appartient bien au plan $\mathcal{P}$.
   On a $\vec{BD}\left(-3;\sqrt{3};2\sqrt{6}\right)$.
   Une représentation paramétrique de la droite $(BD)$ est donc
   $\begin{cases} x=3-3t\\y=t\sqrt{3}\\z=2t\sqrt{6}\end{cases} \quad, t\in \mathbb R$.
   Si $t=0,5$ alors $\begin{cases} x=1,5\\y=0,5\sqrt{3}\\z=\sqrt{6}\end{cases}$. On retrouve les coordonnées du point $J$.
   Le point $J$ appartient bien également à la droite $(BD)$.
   Montrons que les vecteurs $\vec{OH}$ et $\vec{BD}$ ne sont pas orthogonaux (pour montrer que la droite et plan sont sécants).
   $\vec{OH}.\vec{BD}=0+2\times 3+2\times 6=18\neq 0$.
   Remarque : on pouvait également montrer que le point $B$ n’appartenait pas au plan $\mathcal{P}$ ce qui exclut le fait que la droite soit incluse dans le plan.Par conséquent le point $J$ est le point d’intersection de la droite $(BD)$ et du plan $\mathcal{P}$.
   $\quad$
   
   3. Donner une représentation paramétrique de la droite (AD), puis démontrer que le plans $\mathcal{P}$ et la droite (AD) sont sécants en un point K dont on déterminera les coordonnées.
   On a $\vec{AD}\left(3;\sqrt{3};2\sqrt{6}\right)$.
   Une représentation paramétrique de la droite $(AD)$ est donc $\begin{cases} x=-3+3k\\y=k\sqrt{3}\\z=2k\sqrt{6}\end{cases} \quad, k\in \mathbb R$.
   Les coordonnées du point d’intersection de la droite $(AD)$ et de plan $\mathcal{P}$ sont solutions du système :
   $\begin{align*} \begin{cases}x=-3+3k\\y=k\sqrt{3}\\z=2k\sqrt{6}\\2y\sqrt{3}+z\sqrt{6}-9=0\end{cases} &\iff \begin{cases} x=-3+3k\\y=k\sqrt{3}\\z=2k\sqrt{6}\\6k+12k-9=0\end{cases} \\
   &\iff \begin{cases} x=-3+3k\\y=k\sqrt{3}\\z=2k\sqrt{6}\\18k-9=0\end{cases} \\
   &\iff \begin{cases} x=-3+3k\\y=k\sqrt{3}\\z=2k\sqrt{6}\\k=0,5\end{cases}\\
   &\iff \begin{cases} k=0,5\\x=-1,5\\y=0,5\sqrt{3}\\z=\sqrt{6}\end{cases}\end{align*}$
   Le point $K$ a donc pour coordonnées $\left(-1,5;0,5\sqrt{3};\sqrt{6}\right)$.
   $K$ est donc le milieu du segment $[AD]$.
   $\quad$
   
   4. Démontrer que les droites (IJ) et (JK) sont perpendiculaires.
   $\vec{IJ}\left(0;-\sqrt{3};\sqrt{6}\right)$ et $\vec{JK}(-3;0;0)$
   Ainsi $\vec{IJ}.\vec{JK}=0+0+0=0$.
   Ces deux vecteurs sont orthogonaux. Le point $J$ appartient aux droites $(IJ)$ et $(JK)$.
   Ces deux droites dont donc perpendiculaires.
   $\quad$
   
   5. Déterminer précisément la nature de la section du tétraèdre ABCD par le plan $\mathcal{P}$.
   On appelle $L$ le milieu du segment $[AC]$. Ses coordonnées sont $(-1,5;1,5\sqrt{3};0)$.
   Montrons qu’il appartient au plan $\mathcal{P}$ :
   $2\times 1,5\sqrt{3}\times \sqrt{3}+0-9=9-9=0$.
   Ainsi $L$ est l’intersection de la droite $(AC)$ et du plan $\mathcal{P}$.
   La section du tétraèdre $ABCD$ par le plan $\mathcal{P}$ est donc le quadrilatère $IJKL$.
   En utilisant le théorème des milieux dans les triangles $ABC$, $BCD$, $ACD$ et $ABD$ on montre que :
   $IL=\dfrac{AB}{2}=3$, $KJ=\dfrac{AB}{2}=3$, $IJ=\dfrac{DC}{2}=3$ et $KL=\dfrac{DC}{2}=3$
   $IJKL$ est donc un losange. D’après la question 2.d. il possède un angle droit en $J$. C’est par conséquent un carré.
   $\quad$
3. Peut-on placer un point M sur l'arête [BD] tel que le triangle OIM soit rectangle en M ?
On a $\vec{BD}\left(-3;\sqrt{3};2\sqrt{6}\right)$
Une représentation paramétrique de la droite $(BD)$ est donc :
$\begin{cases} x=3-3t\\y=t\sqrt{3}\\z=2t\sqrt{6}\end{cases} \quad ,t\in \mathbb R$.
Ainsi $\vec{OM}\left(3-3t;t\sqrt{3};2t\sqrt{6}\right)$ et $\vec{IM}\left(1,5-3t;t\sqrt{3}-1,5\sqrt{3};2t\sqrt{6}\right)$.
Le triangle $OIM$ est rectangle en $M$
$\iff \vec{OM}.\vec{IM}=0$
$\iff (1,5-3t)(3-3t)+3t^2-4,5t+24t^2=0$
$\iff 4,5-4,5t-9t+9t^2+3t^2-4,5t+24t^2=0$
$\iff 36t^2-18t+4,5=0$
Le discriminant de ce polynôme est $\Delta=-324<0$.
L’équation ne possède pas de solution réelle.
On ne peut donc placer de point $M$ sur l’arête $[BD]$ tel que le triangle $OIM$ soit rectangle en $M$.
$\quad$