Baccalauréat Polynésie 11 septembre 2014 STI2D--STL spécialité SPCL - Correction Exercice 1
Page 2 sur 8
Correction de l'exercice 1 (4 points)
On considère les nombres complexes $Z_{1}$ et $Z_{2}$ : \[Z_{1} = \dfrac{3\sqrt{2}}{1 + \text{i}}\quad \text{et}\quad Z_{2} = \dfrac{4\text{i}}{1 + \text{i}\sqrt{3}}.\]
- Ecrire les nombres $Z_{1}$ et $Z_{2}$ sous forme algébrique et trigonométrique.
- Forme algébrique de $Z_1$ $$\begin{array}{ll} Z_{1} &= \dfrac{3\sqrt{2}}{1 + \text{i}} \\ & = \dfrac{3\sqrt{2}(1 - \text{i})}{(1 + \text{i})(1 - \text{i})}\\ & = \dfrac{3\sqrt{2} - 3\sqrt{2}\text{i}}{ 1^2+1^2 }\\ & = \dfrac{3\sqrt{2} - 3\sqrt{2}\text{i}}{2 }\\ \end{array}$$
- Forme trigonométrique de $Z_1$ Forme trigonométrique de $ Z_1= \dfrac{3\sqrt{2} - 3\sqrt{2}\text{i}}{2 }=\dfrac{3\sqrt{2}}{2} -\text{i} \dfrac{3\sqrt{2}}{2}$:
- Forme algébrique de $Z_2$ $$\begin{array}{ll} Z_{2} &= Z_{2} = \dfrac{4\text{i}}{1 + \text{i}\sqrt{3}} \\ & = \dfrac{4\text{i}(1 - \text{i}\sqrt{3})}{(1 + \text{i}\sqrt{3})(1 - \text{i}\sqrt{3})}\\ & = \dfrac{4\text{i} + 4 \sqrt{3}}{ 1^2+\sqrt 3^2 }\\ & = \dfrac{4 \sqrt{3} 4\text{i}}{4 }\\\end{array}$$
- Forme trigonométrique de $Z_2$ Forme trigonométrique de $Z_2=\sqrt{3} +\text{i}$:
$ Z_1= \dfrac{3\sqrt{2} - 3\sqrt{2}\text{i}}{2 }$.
Module : $|Z_1|=\sqrt{a^2+b^2}=\sqrt{\left(\dfrac{3\sqrt{2}}{2}\right)^2+\left(\dfrac{3\sqrt{2}}{2}\right)^2}=\sqrt{\dfrac{18}{4}+\dfrac{18}{4}}= \sqrt{9}=3$
Argument: $$\left\{ \begin{array}{l } \cos(\theta)=\dfrac{a}{r}= \dfrac{\dfrac{3\sqrt{2}}{2}}{3}= \dfrac{\sqrt 2}{2}\\ \sin(\theta)=\dfrac{b}{r}= \dfrac{\dfrac{-3\sqrt{2}}{2}}{3}= -\dfrac{\sqrt 2}{2} \end{array} \right.$$ Ainsi $\theta=-\dfrac{\pi}{4}$ convient; on a donc: $$Z_1=[3;-\dfrac{\pi}{4}] \text{ ou } Z_1=3\left [\cos\left (-\dfrac{\pi}{4}\right )+i\sin\left (-\dfrac{\pi}{4}\right )\right ]$$La forme exponentielle de $Z_{1}$ est $Z_1= 3e^{-i\frac{\pi}{4}}$
La forme trigonométrique de $Z_1$ est $Z_1=3\left [\cos\left (-\dfrac{\pi}{4}\right )+i\sin\left (-\dfrac{\pi}{4}\right )\right ]$$ Z_2= \sqrt{3} +\text{i}$.
Module : $|Z_2|=\sqrt{a^2+b^2}=\sqrt{\sqrt{3}^2+1^2}=\sqrt{4}=2$
Argument: $$\left\{ \begin{array}{l } \cos(\theta)=\dfrac{a}{r}= \dfrac{\sqrt{3}}{2}\\ \sin(\theta)=\dfrac{b}{r}= \dfrac{1}{2} \end{array} \right.$$ Ainsi $\theta= \dfrac{\pi}{6}$ convient; on a donc: $$Z_2=[2; \dfrac{\pi}{6}] \text{ ou } Z_2=2\left [\cos\left (\dfrac{\pi}{6}\right )+i\sin\left (\dfrac{\pi}{6}\right )\right ]$$La forme exponentielle de $Z_{2}$ est $Z_2= 2e^{i\frac{\pi}{6}}$
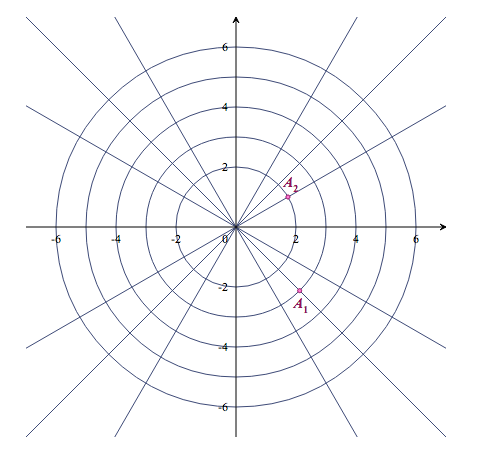
La forme trigonométrique de $Z_2$ est $Z_2=2\left [\cos\left (\dfrac{\pi}{6}\right )+i\sin\left (\dfrac{\pi}{6}\right )\right ]$ - Placer les points A$_{1}$ et A$_{2}$ d'affixes respectives $Z_{1}$ et $Z_{2}$ dans le repère donné en annexe.
- Calculer sous forme algébrique le produit $Z_{1} \times Z_{2}$ et donner sa forme trigonométrique.
- Forme algébrique de $Z_1\times Z_2$ $$\begin{array}{ll} Z_{1}\times Z_2 &= \dfrac{3\sqrt{2} - 3\sqrt{2}\text{i}}{2 }\times ( \sqrt{3} +\text{i}) \\ & = \dfrac{3\sqrt{6}}{2} +\text{i} \dfrac{3\sqrt{2}}{2}- \text{i} \dfrac{3\sqrt{6}}{2} +\dfrac{3\sqrt{2}}{2}\\ & = \dfrac{3\sqrt{2} - 3\sqrt{2}\text{i}}{ 1^2+1^2 }\\ & = \dfrac{3(\sqrt{6}+\sqrt{2})}{2} + \text{i} \dfrac{3(\sqrt{2}-\sqrt{6})}{2}\\\end{array}$$
- Forme trigonométrique de $Z_1\times Z_2$ $$\begin{array}{ll} Z_{1}\times Z_2 &= 3e^{-i\frac{\pi}{4}} \times 2e^{i\frac{\pi}{6}} \\ & = 6 e^{i\left(-\frac{\pi}{4} + \frac{\pi}{6}\right)} \\ & = 6 e^{-i\frac{\pi}{12} } \\\\\end{array}$$
$ Z_1\times Z_2 = \dfrac{3(\sqrt{6}+\sqrt{2})}{2} + \text{i} \dfrac{3(\sqrt{2}-\sqrt{6})}{2}$.La forme trigonométrique de $ Z_1\times Z_2$ est $ Z_1\times Z_2 = 6 e^{-i\frac{\pi}{12} }$ - En déduire les valeurs exactes de $\cos \dfrac{\pi}{12}$ et $\sin \dfrac{\pi}{12}$. On identifie les formes algébrique et trigonométrique de $ Z_1\times Z_2$: $$ Z_1\times Z_2 = 6 e^{-i\frac{\pi}{12} }=6\left [\cos\left (\dfrac{-\pi}{12}\right )+i\sin\left (\dfrac{-\pi}{12}\right )\right ]$$ $$\begin{array}{ll } Z_1\times Z_2&= \dfrac{3(\sqrt{6}+\sqrt{2})}{2} + \text{i} \dfrac{3(\sqrt{2}-\sqrt{6})}{2} \\ &= 6\left [\cos\left (\dfrac{-\pi}{12}\right )+i\sin\left (\dfrac{-\pi}{12}\right )\right ] \end{array}$$ En identifiant les parties réelles et les parties imaginaires on obtient : $$\left\{ \begin{array}{l } Re(Z_1\times Z_2 )=6\cos(\dfrac{-\pi}{12})= 6\cos(\dfrac{\pi}{12})=\dfrac{3(\sqrt{6}+\sqrt{2})}{2} \\ Im(Z_1\times Z_2 )=6\sin(-\dfrac{\pi}{12})=-6\sin(\dfrac{\pi}{12})= \dfrac{3(\sqrt{2}-\sqrt{6})}{2} \end{array} \right.$$
$$\left\{ \begin{array}{l } \cos(\dfrac{ \pi}{12})=\dfrac{ \sqrt{6}+\sqrt{2} }{4} \\ \sin(\dfrac{\pi}{12})= \dfrac{ \sqrt{6}-\sqrt{2} }{4} \end{array} \right.$$
Exercice 2
- Vues: 22090
