BAC STI2D NOUVELLE CALÉDONIE MARS 2014 - Exercice 4

Page 6 sur 7: Exercice 4

Exercice 4 7 points

Fonctions exponentielles

Dans tout l'exercice, on désigne par $\mathbb{R}$ l'ensemble des nombres réels.

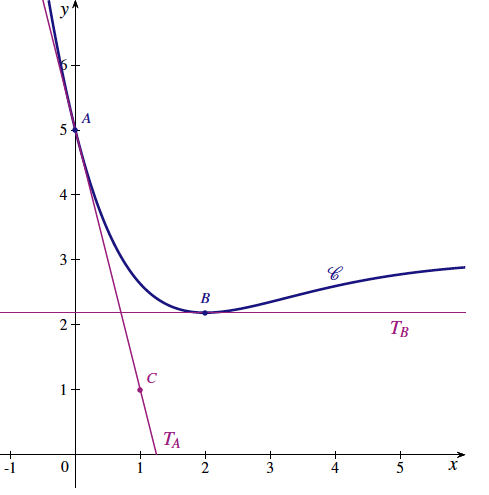
On donne ci-dessous une petite partie de la courbe représentative $\mathcal{C}$ d'une fonction $f$ définie et dérivable sur $\mathbb{R}$, dans un repère orthonormé du plan.

On note $f'$ la fonction dérivée de $f$.

La courbe $\mathcal{C}$ passe par le point $A (0 ; 5)$ et par le point $B$ d'abscisse 2.

La tangente $T_A$ à la courbe au point $A$ passe par le point $C(1 ; 1)$ et la tangente $T_B$ au point $B$ est horizontale.

 

Partie A

Dans ce questionnaire à choix multiples, aucune justification n'est demandée. Pour chacune des questions, une seule des réponses proposées est correcte.

Une bonne réponse rapporte $0,5$ point. Une mauvaise réponse ou l'absence de réponses n'enlève ni ne rapporte aucun point.

On notera sur la copie le numéro de la question et la réponse choisie.

1. La valeur de $f(0)$ est :
   1. $- 4$
   2. $ 4$
   3. $1,2$
   4. autre réponse
2. La valeur de $f'(0)$ est :
   1. $- 4$
   2. $ 4$
   3. $1,2$
   4. autre réponse
3. La valeur de $f'(2)$ est :
   1. $0$
   2. $ 2,1$
   3. $3$
   4. autre réponse
4. Un encadrement de $\displaystyle\int_{0}^2 f(x) \;d x$ par des entiers naturels est : est :
   1. $3 \leqslant \displaystyle\int_{0}^2 f(x) \;d x \leqslant 4$
   2. $5 \leqslant \displaystyle\int_{0}^2 f(x) \;d x \leqslant 7$
   3. $2 \leqslant \displaystyle\int_{0}^2 f(x) \;d x \leqslant 5$
   4. $0 \leqslant \displaystyle\int_{0}^2 f(x) \;d x \leqslant 2$

Partie B

La fonction $f$ représentée dans la PARTIE A est définie sur $\mathbb{R}$ par $f(x) = \left(- x^2 - 2x + 2\right)e^{- x} + 3$.

1. On admet que la limite de la fonction $f$ en $+ \infty$ est 3. Déterminer la limite de $f$ en $- \infty$.
2. On désigne par $f'$ la fonction dérivée de la fonction $f$ et on admet que pour tout nombre réel $x$ appartenant à $\mathbb{R}$, $f'(x) = \left(x^2 - 4\right)e^{- x}$.
   1. Étudier le signe de $f'(x)$ suivant les valeurs de $x$.
   2. En déduire le tableau de variation de la fonction $f$.
3. On considère la fonction $F$ définie sur $\mathbb{R}$ par $F(x) = \left(x^2 + 4x + 2\right)e^{- x} + 3x$. Vérifier que la fonction $F$ est une primitive de la fonction $f$ sur $\mathbb{R}$.
4. On considère le domaine $\mathcal{D}$ du plan limité par la courbe $\mathcal{C}$ l'axe des abscisses et les droites d'équations $x = 0$ et $x = 2$.
   1. Calculer la valeur exacte de l'aire $\mathcal{A}$, exprimée en unités d'aire, du domaine $\mathcal{D}$.
   2. Donner une valeur approchée de $\mathcal{A}$ au centième.