Limites
Limites de fonctions
Limite au voisinage de $+\infty$
Soit $l$ un réel. Dire que $f(x)$ a pour limite $l$ au voisinage de $+\infty$ signifie que tout intervalle ouvert contenant $l$ contient aussi toutes les valeurs de $f(x)$ pour x assez grand.
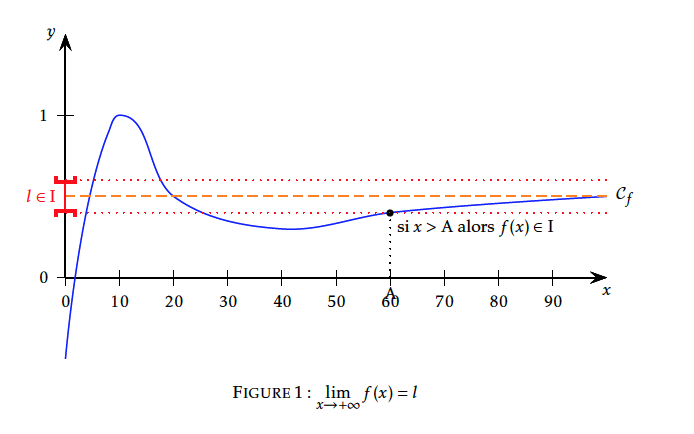
La droite d'équation $y=l$ est une asymptote horizontale à la courbe de $f$ au voisinage de $+\infty$.
Exemples :
- $\lim\limits_{x\to+\infty}\dfrac{1}{x}=0$ et la droite d'équation $y=0$ est asymptote à la courbe de $f$ au voisinage de $+\infty$ (la droite est toujours en dessous de la courbe sur $[0;+\infty[$);
- $\lim\limits_{x\to+\infty}\dfrac{-1}{x}=0$ et la droite d'équation $y=0$ est asymptote à la courbe de $f$ au voisinage de $+\infty$ (la droite est toujours au dessus de la courbe sur $[0;+\infty[$);
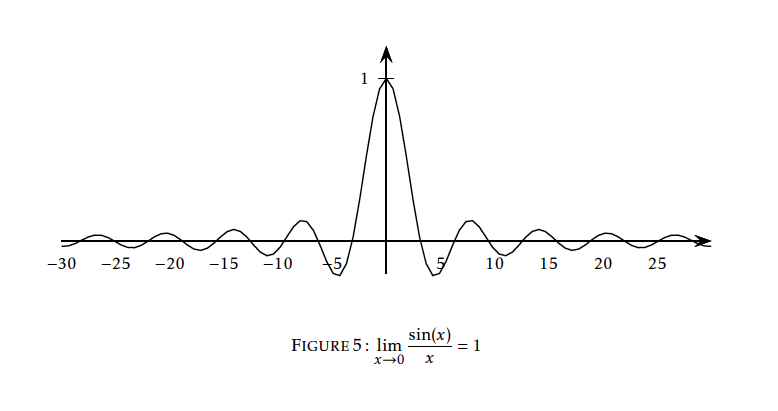
- $\lim\limits_{x\to+\infty}\dfrac{\sin(x)}{x}=0$ et la droite d'équation $y=0$ est asymptote à la courbe de $f$ au voisinage de~$+\infty$ (la courbe coupe la droite en une infinité de points).
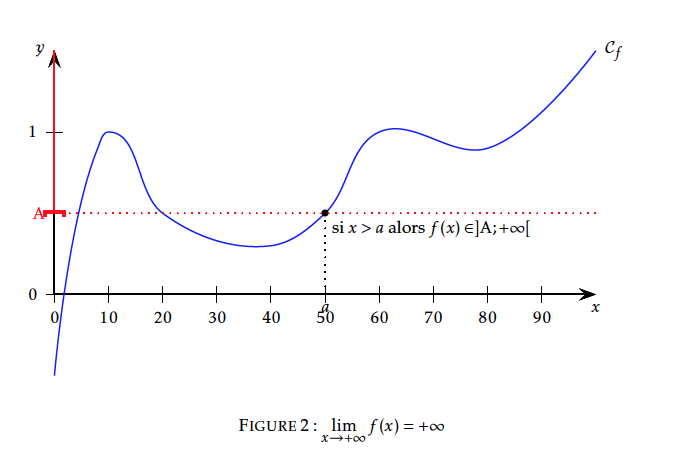
La courbe de $f:x\mapsto x+2+\dfrac{1}{x^2}$ admet une asymptote oblique d'équation $y=x+2$ au voisinage de $+\infty$ et au voisinage de $-\infty$.
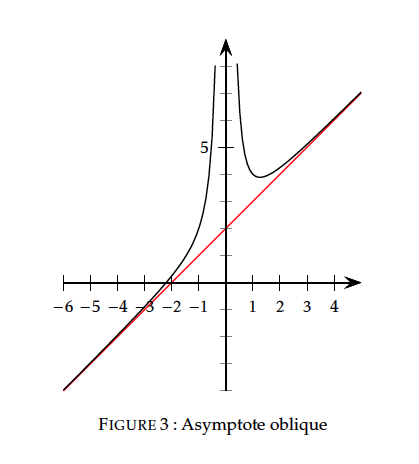
Limite au voisinage d'un réel $a$
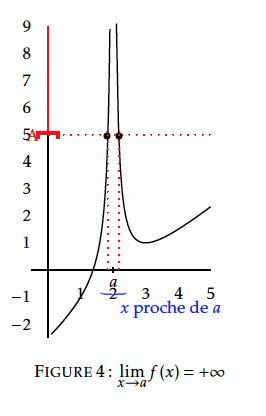
La droite d'équation $x=a$ est une asymptote verticale à la courbe de $f$.
Soit $f$ la fonction définie sur $\mathbb{R}^*$ par $f(x)=\dfrac{\sin(x)}{x}$. On a
$$\begin{array}{ll} \lim\limits_{x\to0}f(x)&=\lim_{x\to0}\dfrac{\sin(x)-0}{x-0} \\ &= \lim\limits_{x\to0}\dfrac{\sin(x)-\sin(0)}{x-0}\\ &=\cos(0) \quad\text{ par définition du nombre dérivé }\\ &=1\\\end{array}$$
Donc$$\lim_{x\to 0}\dfrac{\sin(x)}{x}=1$$
Opérations sur les limites
Dans les théorèmes admis ci-dessous, présentés sous forme de tableaux,$u$ et $v$ sont des fonctions définies sur un même intervalle $I$ et $\bigcirc$ désigne $+\infty ,-\infty$ ou un nombre réel $a$; $L$ et $L'$ sont des nombres réels.
somme
Comment déterminer $\displaystyle\lim_{x \to \bigcirc}[u(x)+v(x)]$? $$\begin{array}{ |c|c|c|c|c|c|c| } \hline \text{ Si } \displaystyle\lim_{x \to \bigcirc}u(x)& L\in \mathbb{R} & L & L & +\infty & +\infty & -\infty \\ \hline \text{ et } \displaystyle\lim_{x \to \bigcirc} v(x) & L'\in \mathbb{R} & +\infty & -\infty & +\infty & -\infty & -\infty \\ \hline \text{ alors }\displaystyle\lim_{x \to \bigcirc}[u(x)+v(x)] & L+L' & +\infty & -\infty & +\infty & ? & -\infty \\ \hline \end{array} $$ Les points d'interrogation ( ?) signalent les cas indéterminés. Ce sont des cas pour lesquels une étude spécifique doit être menée pour déterminer une éventuelle limite.
Cas du produit d'une fonction par une constante
On suppose que la constante $k$ n'est pas nulle. Comment déterminer $\displaystyle\lim_{x \to \bigcirc}[ku(x) ]$?
$$\begin{array}{ |c|c|c|c|c|c| } \hline \text{ Si }\displaystyle\lim_{x \to \bigcirc}u(x) & L\in \mathbb{R} & +\infty & +\infty & -\infty & -\infty \\ \hline \text{ alors } \displaystyle\lim_{x \to \bigcirc} [ku(x)] & kL & +\infty \text{ si } k>0 & -\infty \text{ si } k < 0 & -\infty \text{ si } k > 0 & +\infty \text{ si } k < 0 \\ \hline \end{array} $$
Cas du produit de deux fonctions
Comment déterminer $\displaystyle\lim_{x \to \bigcirc}[u(x)\times v(x) ]$? $$\begin{array}{ |c|c|c|c|c|c| } \hline \text{ Si } \displaystyle\lim_{x \to \bigcirc}u(x)& L\in \mathbb{R} & L\neq 0 & 0 & +\infty \text{ ou } -\infty \\ \hline et \displaystyle\lim_{x \to \bigcirc} v(x) & L' & +\infty \text{ ou } -\infty& +\infty \text{ ou } -\infty& +\infty \text{ ou } -\infty \\ \hline alors \displaystyle\lim_{x \to \bigcirc} [u(x)\times v(x)] & LL' & \pm\infty & \textbf{?} & \pm\infty \\ \hline \end{array}$$ $ \pm \infty$ correspond soit à $+\infty$, soit à $-\infty$. Le signe + ou - s'obtient de façon évidente dans chaque exemple.
Cas de l'inverse :
Comment déterminer $\displaystyle\lim_{x \to \bigcirc} \dfrac{1}{u(x)} $?
$$ \begin{array}{ |c|c|c|c|c| } \hline \text { Si } \displaystyle\lim_{x \to \bigcirc}u(x)& L\neq 0 & 0 & +\infty \text{ ou } -\infty \\ \hline alors \displaystyle\lim_{x \to \bigcirc} \dfrac{1}{u(x)} & \dfrac{1}{L} &\text{ voir le théorème ci dessous } & 0 \\ \hline \end{array} $$
- Si $\displaystyle\lim_{x \to \bigcirc}u(x)=0$ et si au voisinage de $\bigcirc$ on a $u(x)>0$, alors on a $\displaystyle\lim_{x \to \bigcirc} \dfrac{1}{u(x)} =+\infty$
- Si $\displaystyle\lim_{x \to \bigcirc}u(x)=0$ et si au voisinage de $\bigcirc$ on a $u(x)<0$, alors on a $\displaystyle\lim_{x \to \bigcirc} \dfrac{1}{u(x)} =-\infty$
Cas du quotient :
Sur tout intervalle où le quotient $\dfrac{u(x)}{v(x)}$ est défini, on remarque que $\dfrac{u(x)}{v(x)}=u(x)\times \dfrac{1}{v(x)}$ et on utilise les théorèmes de l'inverse $\dfrac{1}{v(x)}$ et la limite d'un produit.
Limite d'une fonction composée
Un exemple ?
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=\sqrt{3x^2+5}$. Cherchons $\displaystyle\lim_{x \to-\infty}f(x)$.
On a $\displaystyle\lim_{x \to-\infty}3x^2+5=+\infty$ et $\displaystyle\lim_{y \to +\infty}\sqrt{y}=+\infty$ donc par composée: $\displaystyle\lim_{x\to-\infty}\sqrt{3x^2+5}=+\infty$
Limites et ordre
Si $f(x)< g(x)$ alors $l \leq l'$
Soit $I$ un intervalle ouvert contenant $l$, on doit montrer que $I$ contient tous les réels $g(x)$ pour $x$ assez grand. Par hypothèse,
- $\lim\limits_{x \to +\infty}f(x)=l$ donc $I$ contient tous les réels $f(x)$ pour $x$ assez grand, plus précisément, il existe un réel $A$ tel que si $x>A$ alors $f(x)\in I$.
- $\lim\limits_{x \to +\infty}h(x)=l$ donc $I$ contient tous les réels $h(x)$ pour $x$ assez grand, plus précisément, il existe un réel $B$ tel que si $x>B$ alors $h(x)\in I$.
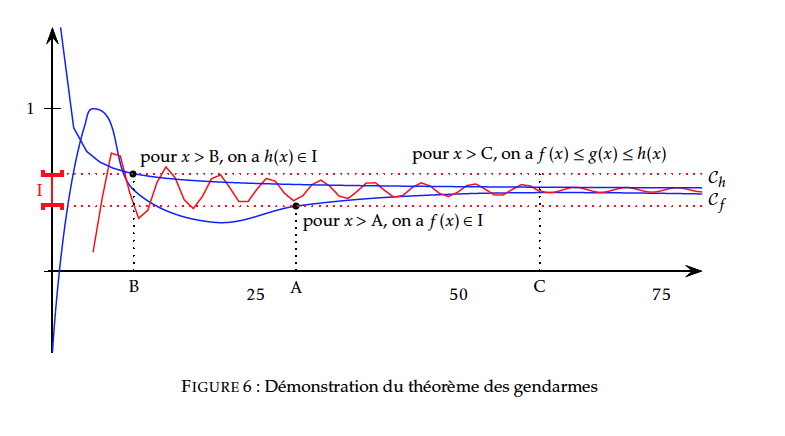
Soit deux fonctions $f$ et $g$ telles que $f\leq g $ au voisinage de $a$ (réel ou $\pm\infty$),
- si $\lim\limits_{x\to a}f(x)=+\infty$ alors $\lim\limits_{x\to a}g(x)=+\infty$;
- si $\lim\limits_{x\to a}g(x)=-\infty$ alors $\lim\limits_{x\to a}f(x)=-\infty$.
EXERCICES
Avec les définitions
Exercice
On considère la fonction $f$ définie sur $]0,+\infty[$ par $f(x)=\dfrac{2x^2+1}{x^2}$
- Donner des valeurs approchées à $10^{-3}$ près de $f(1)$, $f(32)$, $f(320)$ et $f(3232)$.
- Observer la représentation graphique de $f$ donnée par une calculatrice ou un ordinateur. Quelle conjecture peut-on faire sur la limite de $f$ en $+\infty$ ?
- On considère l'intervalle ouvert de centre 2 et de rayon 0,01 , c'est-à -dire $]1,99 ; 2,01[$ . Démontrer que pour $x > 10$ , $f(x)\in ]1,99 ; 2,01[$ (On pourra écrire $f(x)$ sous la forme $f(x)=2+1/x^2$ )
- On considère l'intervalle $]2-r, 2+r[$ avec $r>0$. Montrer que pour $x$ supérieur à un certain $x_0$ à déterminer en fonction de $r$ , tous les $f(x)$ appartiennent à l'intervalle $]2-r,2+r[$.
- Démontrer que $\lim\limits_{x\to+\infty} f(x)=2$
Exercice
On considère la fonction $g$ définie sur $\mathbb{R}$ par $3x^3+x^2$
- Donner les valeurs de $g(32)$, $g(320)$ et $g(3232)$.
- Observer la représentation graphique de $g$ donnée par une calculatrice ou un ordinateur. Quelle conjecture peut-on faire sur la limite de $g$ en $+\infty$ ?
- On considère l'intervalle $]100; +\infty[$ . Démontrer que pour $x > 10$, $f(x)\in\ ]100,+\infty[$.
- On considère un intervalle $]A,+\infty[$ , avec A > 0. Montrer que pour $x$ supérieur à $\sqrt{A}$ , tous les $f(x)$ appartiennent à l'intervalle $]A ; +\infty[$ .
Exercice
Soit $h$ définie sur $\mathbb{R}$ par $h(x)=-2x+3$ Démontrez que $\lim\limits_{x\to+\infty}f(x)=-\infty$
Exercice
On considère la fonction $h$ définie sur $]1,+\infty[$ par $h(x)=2+\dfrac{3}{(x-1)^2}$
- Justifiez que $h$ est bien définie sur $]1,+\infty[$.
- Observer la représentation graphique de $h$ donnée par une calculatrice ou un ordinateur. Quelle conjecture peut-on faire sur la limite de $h$ en $1$ ?
- On considère l'intervalle $]1000; +\infty[$ . Donnez une condition suffisante portant sur $x$ pour que $h(x)\in\ ]1000,+\infty[$.
- On considère un intervalle $]A,+\infty[$ , avec A > 2. Donnez une condition suffisante portant sur $x$ pour que $h(x)\in ]A ; +\infty[$ .
- Justifiez que $\lim\limits_{x\to 1} h(x)=+\infty$.
Avec les théorèmes
Exercice
Limite en zéro Soit $f~:~x\mapsto \dfrac{|x|}{x}$. Étudiez sa limite en zéro.
Exercice
De la géométrie pour calculer une limite
Voici une première méthode de calcul de $\lim\limits_{x \to 0}\dfrac{\sin x}{x}$. Pourquoi suffit-il d'étudier la limite pour des valeurs de $x>0$ ? Utilisez une figure pour obtenir que, pour tout $x\in]0,\pi/2[$,
$$\sin x< x <\tan x$$ Déduisez-en un encadrement de $\dfrac{\sin x}{x}$ pour tout $x\in]0,\pi/2[$ et concluez après avoir étudié la parité de la fonction.
Exercices : Limites trigonométriques
En supposant connu le résultat de l'exercice précédent, calculez $\lim\limits_{x \to 0}\dfrac{\tan x}{x}$ et $\lim\limits_{x \to 0}\dfrac{1-\cos x}{x^2}$
Pour la 2éme, utilisez la formule bien connue $\cos(2a)=1-2\sin^2(a)$
Exercice : Limite et radicaux
Calculez :
- $ \lim\limits_{x\to 0}\dfrac{\sqrt{1+x}-1}{x}$
- $ \lim\limits_{x\to +\infty}{\sqrt{x^2+1}-x} $
- $ \lim\limits_{x\to 0}\dfrac{x^2}{1-\sqrt{1-x^2}}$
Calculs stakhanovistes
Applications directes du cours
Exercice
Étudier les limites des fonctions suivantes au voisinage de $+\infty$:
- $x^2-5x+6$;
- $-4x^2+6x-7$;
- $\dfrac{2x+1}{x-1}$;
- $\dfrac{2x^2-3x+5}{x^3+x-3}$;
- $\dfrac{x^3}{x^2+1}-x$;
- $\dfrac{2x-\sqrt{x}}{\sqrt{x}-3}$.
Exercice
Étudier les limites des fonctions suivantes au voisinage de $+\infty$:
- $\dfrac{x+\sin(x)}{-2x+\cos(x)}$;
- $2x-\sqrt{x^2+3x-1}$;
- $\dfrac{\sqrt{x^2-2x+3}}{x}$.
Étudier les limites des fonctions suivantes au voisinage de $a$:
- $\dfrac{x+4}{x^2+3x+2}$ en $a=-2$;
- $\dfrac{x+2}{x^2+3x+2}$ en $a=-2$;
- $\dfrac{-x^2+x+6}{2x^2-5x+2}$ en $a=2$;
- $\dfrac{\sqrt{x+1}}{x}$ en $a=0$;
- $\dfrac{\sqrt{x+1}-1}{x}$ en $a=0$;
- $\dfrac{\sqrt{x+4}-2}{x}$ en $a=0$;
- $\tan(x)$ en $a=\dfrac{\pi}{2}$;
- $\dfrac{\sin(3x)}{x}$ en $a=0$.
Exercice
Soit $f$ la fonction définie par : \[f(x)=\dfrac{-x^3+2x^2-x+3}{x^2+1} \,.\]
- Déterminer trois réels $a$, $b$ et $c$ tels que $f(x)=ax+b+\dfrac{c}{x^2+1}$.
- Calculer la limite de $f(x)-(ax+b)$ en $+\infty$ puis en $-\infty$.
- En déduire que la courbe représentative de $f$, $\mathcal{C}$ admet une asymptote oblique $\Delta$ en $-\infty$ et en $+\infty$.
- Étudier les positions relatives de $\mathcal{C}$ et de $\Delta$.
Approfondissement
Exercice
Étudier les limites des fonctions suivantes :
- $\sqrt{x^2+1}-\sqrt{x^2-1}$ en $+\infty$;
- $x\left(\sqrt{\dfrac{x+1}{x-1}}-1\right)$ en $+\infty$;
- $\dfrac{\sqrt{x^2+1}-\sqrt{x+3}}{x^2-2x}$ en $2$;
- $\dfrac{\tan(x)}{x}$ en $0$;
- $\dfrac{\sin(ax)}{\sin(bx)}$ en $0$ avec $ab\neq0$;
- $x\sin\left(\dfrac{1}{x}\right)$ en $+\infty$.
Exercice
Étudier selon les valeurs de $a$ et de $b$ les limites de
- $f:x\mapsto\sqrt{x^2+5x+1}+ax+b$ en $+\infty$ et en $-\infty$
- $g:x\mapsto\dfrac{ax^2-(2a+1)x+2}{x-1}$ en 1.
Exercice
Question de cours (Métropole, Nouvelle Calédonie novembre 2007)
- Soit $f$ une fonction réelle définie sur $[a~;~+ \infty[$. Compléter la phrase suivante : « On dit que $f$ admet une limite finie $\ell$ en $+ \infty$ si ... »
- Démontrer le théorème « des gendarmes » : soient $f,~g$ et $h$ trois fonctions définies sur $[a~;~+ \infty[$ et $\ell$ un nombre réel. Si $g$ et $h$ ont pour limite commune $\ell$ quand $x$ tend vers $+ \infty$, et si pour tout $x$ assez grand $g(x) \leqslant f(x) \leqslant h(x)$, alors la limite de $f$ quand $x$ tend vers $+ \infty$ est égale à $\ell$.
Recettes à Bac
Comment étudier la position relative de deux courbes ?
Soit $C_f$ la courbe d'équation $y=f(x)$ et $C_g'$ la courbe d'équation $y=g(x)$. Pour étudier la position relative de $C_f$ et $C_g$, il faut étudier le signe de $f(x)-g(x)$. En effet, si nous obtenons par exemple $f(x)-g(x)\geq 0$ sur l'intervalle $I$, alors $f(x)\geq g(x)$ sur $I$ et donc $C_f$ est au-dessus de $C_g$ sur $I$.
Comment montrer qu'une courbe admet une asymptote d'équation $y=ax+b$ au voisinage de $\omega$ ?
Il suffit de montrer que $\left[f(x)-(ax+b)\right]$ tend vers 0 quand $x$ tend vers $\omega$.
Asymptote horizontale
\[\lim_{x\to +\infty}f(x)=2 \,.\] Soit $f$ la fonction définie par \[f(x) = \dfrac{x^{2} - x +1}{x^{3} + 1}\,.\] Montrer que $\lim\limits_{x\to+\infty}f(x) = 0$. Interpréter graphiquement ce résultat.
Asymptote verticale
\[\lim_{x\to 2 \atop x>2}f(x)= + \infty \text{ et } \lim_{x\to 2 \atop x<2}f(x)= - \infty \,.\] Soit $f$ la fonction définie par \[f(x) = \dfrac{x^{2} - x +1}{x - 1}\,.\] Étudier les limites de $f$ au voisinage de 1 puis interpréter graphiquement ce résultat.
Asymptote oblique
\[\lim_{x\to -\infty}\left(f(x)-(mx+p)\right)=0 \text{ et } \lim_{x\to +\infty}\left(f(x)-(mx+p)\right)= 0\,.\] Soit $f$ la fonction définie sur $]0;+\infty[$ par \[f(x) = \dfrac{\sqrt{x+1}}{x^2} + 2x -1\,.\] Prouver que la droite $\Delta$ d'équation $y=2x-1$ est une asymptote oblique à la courbe représentative de $f$ au voisinage de $+\infty$.
Comment montrer qu'une fonction est paire ?
Il faut vérifier que l'ensemble de définition de $f$ est symétrique par rapport à zéro puis que pour tout réel $x$ de l'ensemble de définition $f(-x)=f(x)$. Nous en déduisons que la courbe est symétrique par rapport à l'axe des ordonnées. Il suffira donc d'étudier la fonction sur la << moitié >> de l'ensemble de définition, puis de déduire le reste de la courbe par symétrie.
Comment montrer qu'une fonction est impaire ?
cf le paragraphe précédent en remplaçant $f(-x)=f(x)$ par $f(-x)=-f(x)$ et <<~symétrique par rapport à l'axe des ordonnées~>> par << symétrique par rapport à l'origine du repère >>.
Comment montrer qu'une courbe admet le point $A(a,b)$ comme centre de symétrie~?
Faites avant tout un dessin pour visualiser que $A$ est le milieu du segment $[MM']$ avec $M (x,f(x) )$ et $M' (x',f(x') )$. Alors d'une part $\dfrac{x+x'}{2}=a$, donc $x'=2a-x$ et d'autre part $\dfrac{f(x)+f(x')}{2}=b$, $i.e.$ $$f(x)+f(2a-x)=2b$$
Comment montrer qu'une fonction est périodique ?
Il s'agit de trouver un réel $T$ tel que pour tout réel $x$ appartenant à l'ensemble de définition de $f$, alors $$f(x+T)=f(x)$$ Il suffira alors d'étudier la fonction sur un intervalle de longueur $T$, par exemple $[0,T]$, puis de déduire le reste de la courbe par des translations successives de vecteur $k\vec{i}$, avec $k\in \mathbb{Z}$. Vous connaissez bien sûr la fonction sinus qui vérifie $\sin(x+2\pi)=\sin x$ pour tout réel $x$ et qui est donc $2\pi$-périodique.
Comment étudier le signe d'une expression ?
Vaste problème...Retenir malgré tout qu'en règle général, nous savons étudier le signe d'un produit ou d'un quotient de polynômes du 1er ou du 2nd degré, d'exponentielles ( qui sont toujours positives ), de cosinus ou de sinus, de logarithmes népériens...
Vous chercherez donc en général à factoriser ou à réduire au même dénominateur votre expression. Si cela s'avère impossible algébriquement, on vous suggérera d'étudier une fonction. Alors soit elle admettra comme extremum zéro, soit vous déterminerez une approximation de la valeur d'annulation de $f$ grâce au théorème de la bijection et vous conclurez à l'aide du tableau de variations.
Qu'est-ce qu'une fonction croissante sur $I$ ?
C'est une fonction qui conserve l'ordre sur $I$.
Comment lever une indétermination ?
Il n'y a pas une méthode mais des méthodes. Il ne s'agit donc pas d'apprendre par c\oe ur des recettes (tiens tiens...), ce qui vous induirait à écrire de grosses sottises. Vous pouvez dans un premier temps repérer des termes <<~négligeables~>> devant d'autres et factoriser par le plus <<~fort~>> (c'est le cas par exemple des fonctions rationnelles au voisinage de $+\infty$ ou $-\infty$). Vous pouvez minorer ou majorer par des valeurs permettant de conclure à l'aide des théorèmes de comparaison (c'est le cas de la fonction cosinus qui vérifie \[-1\leq\cos x\leq 1\] pour tout réel $x$ et donc \[-\dfrac{1}{x}\leq \dfrac{\cos x}{x}\leq \dfrac{1}{x}\] pour $x\geq 0$ et finalement \[\displaystyle\lim_{x\to+\infty}\dfrac{\cos x}{x}=0\] par application du théorème des gendarmes. Vous pouvez utiliser les propriétés algébriques de certaines fonctions pour retrouver des limites connues ( $x^2+1=\sqrt{x^2+1}\sqrt{x^2+1}$...) Dans le cas de l'étude de limites de fonctions irrationnelles, le recours à la quantité conjuguée peut s'avérer utile. Dans les cas désespérés, vous pouvez essayer de reconnaàître la limite d'un taux de variation et donc utiliser la dérivée associée.
- Vues: 18488
