DM 01 TS4

• Ensemble de définition : Il faut qu'aucun des dénominateurs ne s'annule, donc l''ensemble de définition est $\mathscr{D}=\mathbb{R}\setminus\left\{-\dfrac{5}{3}~;~\dfrac{1}{5}\right\}$.
• On suppose que $x\in\mathscr{D}$. (on peut alors raisonner par équivalences) Alors : $$\begin{array}{rl} (I)&\Leftrightarrow \dfrac{2x+5}{3x+5}- \dfrac{x-1}{5x-1} \geqslant 0\\ &\Leftrightarrow \dfrac{(2x+5)(5x-1)-(3x+5)(x-1)}{(3x+5)(5x-1)}\geqslant 0\\ &\Leftrightarrow \dfrac{\left(10x^2-2x+25x-5\right)-\left(3x^2-3x+5x-5\right)}{(3x+5)(5x-1)}\geqslant 0\\ & \Leftrightarrow \dfrac{7x^2+21x}{(3x+5)(5x-1)}\geqslant 0\\ & \Leftrightarrow \dfrac{7x(x+3)}{(3x+5)(5x-1)}\geqslant 0 \end{array}$$
  Remarque : il faut absolument factoriser !!!
• On renseigne un tableau de signes : Le numérateur s'annule pour $x=-3$ ou $x=0$.
  
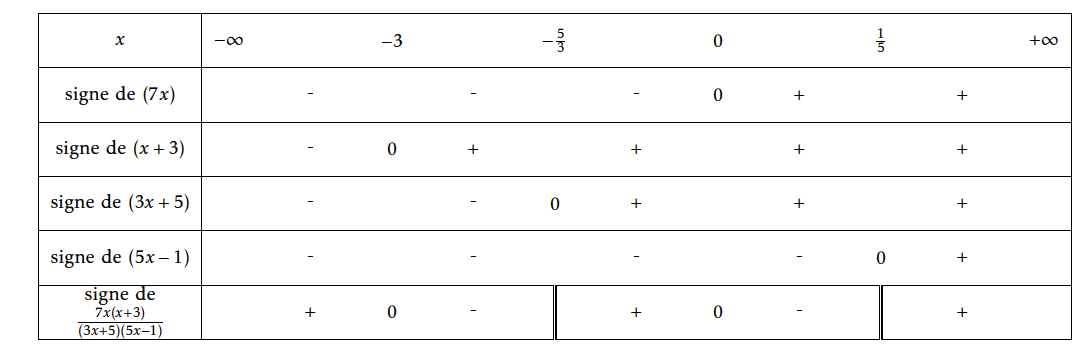
• Conclusion : ce quotient doit être supérieur ou égal à 0. L'ensemble des solutions est : $\mathscr{S}=\left]-\infty~;~-3\right]\cup\left]-\dfrac{5}{3}~;~0\right]\cup\left]\dfrac{1}{5}~;~+\infty\right[$

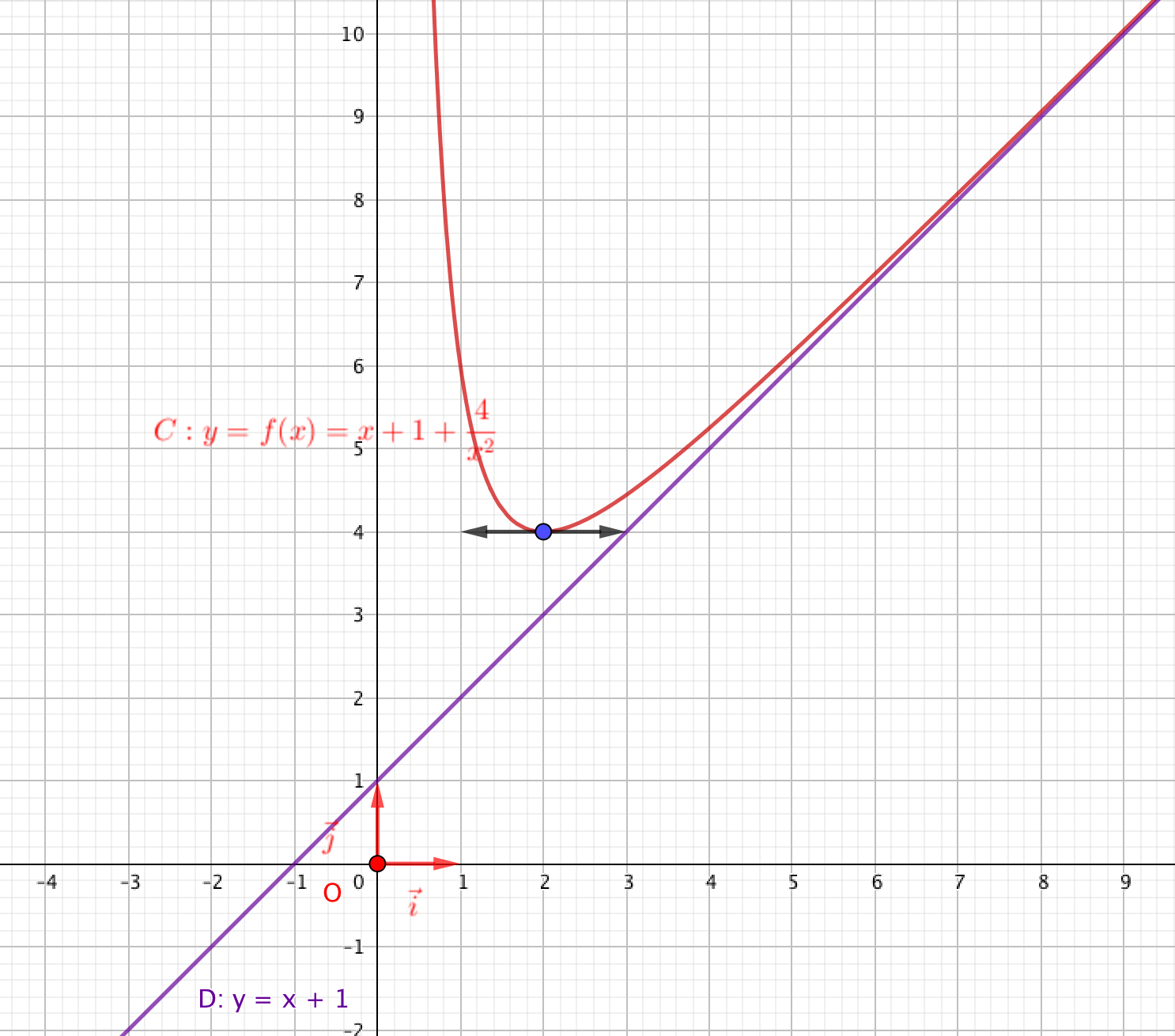
Soit $f$ la fonction définie sur $]0~;~+\infty[$ par \[f(x)=x+1+\dfrac{4}{x^2}\]. On note $\mathscr{C}$ la courbe représentative de $f$.

1. Calculer $f'(x)$ et l'écrire sous forme de fraction rationnelle.
$f$ est dérivable sur $]0~;~+\infty[$ comme somme de fonctions dérivables. Pour tout $x>0$, $f(x)=x+1+4\times \dfrac{1}{x^2}$, donc $f'(x)=1+0+4\times \left(-\dfrac{2}{x^3}\right)=1-\dfrac{8}{x^3}=\dfrac{x^3-8}{x^3}$
2. Vérifier que $a^3-b^3=(a-b)(a^2+ab+b^2)$.
$(a-b)(a^2+ab+b^2)=a^3+a^b+ab^2-a^2b-ab^2-b^3=a^3-b^3$ donc $$a^3-b^3=(a-b)(a^2+ab+b^2)$$
3. En déduire la factorisation de $f'(x)$.
$f'(x)=\dfrac{x^3-8}{x^3}=\dfrac{x^3-2^3}{x^3}=\dfrac{(x-2)(x^2+x+2)}{x^3}$.
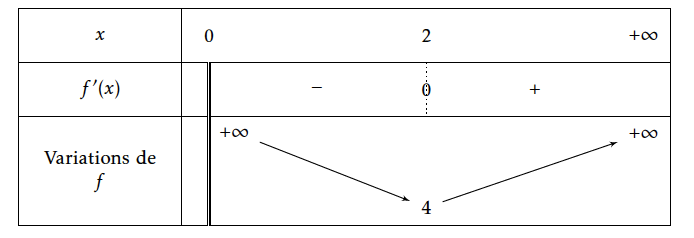
4. En déduire les variations de $f$.
Pour étudier les variations de $f$, on étudie le signe de sa dérivée sur l'intervalle $]0~;~+\infty[$.
• $x>0$ donc $x^3>0$
• $x^2+x+2$ a une discriminant égal à -7, négatif, donc $x^2+x+2>0$ pour $x>0$
• $x-2>0$ pour $x>2$ et $x-2<0$ pour $x<2$
On en déduit que $f'(x)\leqslant 0$ pour $0<x\leqslant 2$ et $f'(x)\geqslant 0$ pour $x\geqslant 2$.

Tableau de variation :

1. On note $\mathscr{D}$ la droite d'équation $y=x+1$. En étudiant le signe de $f(x)-(x+1)$, trouver la position relative de $\mathscr{C}$ et de $\mathscr{D}$.
Pour tout $x>0$, $f(x)-(x+1)=\dfrac{4}{x^2}$ donc $f(x)-(x+1)>0$ et $f(x)>x+1$.

$\mathscr{C}$ est donc au-dessus de $\mathscr{D}$.
1. Construire la droite $\mathscr{D}$ et la courbe représentative de $f$.

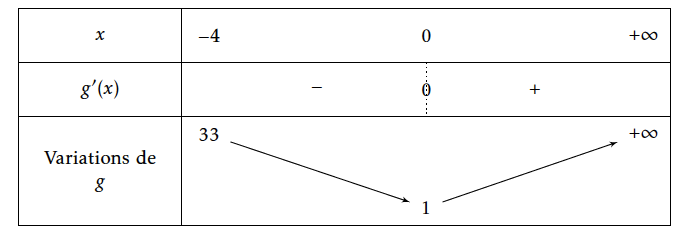
1. Soit $g$ la fonction définie sur $]-4~;~+\infty[$ par : \[g(x)=x^3+6x^2+1.\]
   1. Déterminer les variaions de $g$ sur son ensemble de définition.
   $g$ est dérivable comme polynôme ; $g'(x)=3x^2+12x= 3x(x+4) $.
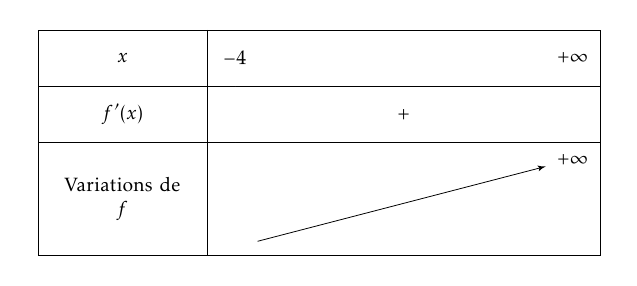
   Ls racines sont -4 et 0.
   Sur $]-4~;~0]$, $g'(x)$ est su signe opposé à celui du coefficient de $x^2$ donc négatf. Sur $[0~;~+\infty[$, $g'(x)\geqslant 0$.
   
   2. En déduire le signe de $g(x)$.
   Le minimum de $g$ est 1, donc $g(x)>0$ sur $]-4~;~+\infty[$.
2. Soit $f$ la fonction définie sur $]-4~;~+\infty[$ par \[f(x)=\dfrac{x^3-2}{x+4}\].
   1. Déterminer $f'(x)$. $f$ est dérivable comme fonction rationnelle (quotient de polynômes).
   $f=\dfrac{u}{v}$ avec $\begin{cases}u(x)=x^3-2\\v(x)=x+4\end{cases}$. $f'=\dfrac{u'v-v'u}{v^2}$ avec $\begin{cases}u'(x)=3x^2\\v'(x)=1\end{cases}$.
   $f'(x)=\dfrac{3x^2(x+4)-\left(x^3-2\right)}{(x+4)^2}=\dfrac{2x^3+12x^2+2}{(x+4)^2}=\dfrac{2g(x)}{(x+4)^2}$.
   2. En déduire les variations de $f$ ; dresser le tableau de variation de $f$.
   $f'$ est donc du signe de g ; par conséquent, $f'$ est positive sur $]-4~;~+\infty[$ ; $f$ est donc croissante sur cet intervalle.