Baccalauréat S Polynésie 9 septembre 2015 - Correction Exercice 2

Page 4 sur 10: Correction Exercice 2

Correction de l'exercice 2 (5 points)

Commun à tous les candidats

Partie A

On étudie une maladie dans la population d'un pays. On a constaté que le taux, en nanogrammes par millilitre $\left(\text{ng.mL}^{-1}\right)$, d'une substance Gamma présente dans le sang est plus élevé chez les personnes atteintes de cette maladie que chez les personnes qui n'en sont pas atteintes.

1. Le taux de cette substance Gamma dans la population des personnes qui ne sont pas atteintes par la maladie est modélisé par une variable aléatoire $T$ qui suit la loi normale d'espérance $\mu = 40$ et d'écart-type $\sigma = 8$. On choisit au hasard une personne parmi celles qui ne sont pas atteintes par la maladie étudiée. Calculer la probabilité que le taux dans le sang de la substance Gamma soit supérieur à 60 ng.mL$^{-1}$.
On veut calculer $P(T \ge 60) = 0,5 – P(40 \le T \le 60) \approx 0,0062$


2ND DISTR 2NORMALFRép( -10^(99) , \1,$\2$,$\3$)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(-10^{99},\1,\2,\3) \approx \4$$

$$P( \5 \leq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
2. Des études ont mis en évidence que le taux moyen de la substance Gamma chez les personnes atteintes par la maladie étudiée est de 50 ng.mL$^{-1}$ et que 10% d'entre elles ont un taux de substance Gamma inférieur à 43 ng.mL$^{-1}$. On appelle $T'$ la variable aléatoire qui modélise le taux de la substance Gamma en ng.mL$^{-1}$ chez une personne atteinte par la maladie étudiée. On admet que $T'$ suit la loi normale d'espérance $\mu'$ et d'écart-type $\sigma'$. Préciser la valeur de $\mu'$ et déterminer la valeur de $\sigma'$.
D’après l’énoncé, on a $\mu’=50$.
On sait également que :
$\begin{align*} P(T’ \le 43) = 0,1 & \Leftrightarrow P\left(\dfrac{T’-50}{\sigma’} \le \dfrac{43-50}{\sigma’}\right)=0,1 \\\\
&\Leftrightarrow P\left(\dfrac{T’-50}{\sigma’} \le -\dfrac{7}{\sigma’}\right) = 0,1
\end{align*}$
Or la variable aléatoire $\dfrac{T’-50}{\sigma’}$ suit la loi normale centrée réduite.
Par conséquent à l’aide de la touche Inverve Loi Normale on obtient $-\dfrac{7}{\sigma’} \approx -1,2816$ soit $\sigma’ \approx 5,4621$.
$\quad$

Partie B

Pour dépister chez une personne la maladie étudiée, on effectue une prise de sang. On considère que le dépistage est positif si le taux de la substance Gamma est supérieur ou égal à 45 ng.mL$^{-1}$. Une personne étant choisie au hasard dans la population, on appelle :

• $M$ l'évènement « le patient est atteint par la maladie étudiée »  ;
• $D$ l'évènement « le patient a un dépistage positif».

On admet que :

• 82% des personnes atteintes par la maladie étudiée ont un dépistage positif ;
• 73% des personnes non atteintes par cette maladie ont un dépistage négatif.

On sait de plus que 10% de la population étudiée est atteinte par cette maladie.

1. Démontrer que la probabilité qu'un patient ait un dépistage positif est de $0,325$.
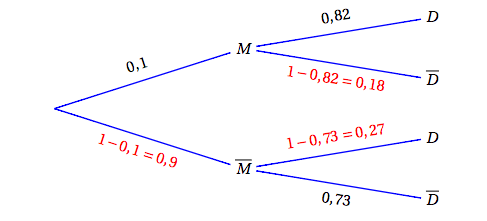On peut résumer la situation par un arbre pondéré : D’après la formule des probabilités totales, on a alors :
$\begin{align*} p(D)&=p(M\cap D) + p\left(D \cap \overline{M}\right) \\\\
&=0,1 \times 0,82 + 0,9 \times 0,27 \\\\
&=0,325
\end{align*}$
$\quad$
2. Calculer $P_{\overline{D}}(M)$. Interpréter ce résultat.
$\begin{align*} p_{\overline{D}}(M) &= \dfrac{p\left(M \cap \overline{D}\right)}{p\left(\overline{D}\right)} \\\\
&= \dfrac{0,1 \times 0,18}{1-0,325}\\\\
&=\dfrac{2}{75}\\\\
&\approx 0,0267
\end{align*}$
Cela signifie donc qu’environ $2,67\%$ des individus ayant un dépistage négatif sont atteints par la maladie étudiée.
$\quad$
3. Un patient a un dépistage positif. Le médecin le rassure en lui indiquant qu'il n'a qu'une chance sur quatre d'avoir contracté la maladie. Qu'en pensez- vous ?
Calculons :
$\begin{align*} p_D(M) &= \dfrac{p(D\cap M)}{p(D)} \\\\
&= \dfrac{0,1 \times 0,82}{0,325} \\\\
& = \dfrac{82}{325} \\\\
& \approx 0,2523
\end{align*}$
Il y a donc effectivement environ une chance sur quatre que le patient ait contracté la maladie.
$\quad$

Partie C

On a $n=300$ et $p=0,82$
Ainsi $n\ge 30$, $np=246\ge 5$ et $n(1-p)=54\ge 5$.
Les conditions sont donc vérifiées pour déterminer un intervalle de fluctuation asymptotique. Le seuil choisi sera de $95\%$

$$\begin{align*} I_{300} &= \left[0,82-1,96\sqrt{\dfrac{0,82 \times 0,18}{300}};0,82+1,96\sqrt{\dfrac{0,82 \times 0,18}{300}}\right] \\\\
& \approx[0,77;0,87]
\end{align*}$$

Or la fréquence observée quand les personnes ne sont pas à jeun est $f=0,74 \notin I_{300}$

Ainsi ce dépistage ne peut pas, au risque de $5\%$, être effectué sur des personnes qui ne sont pas à jeun.