Continuité et équations
Comment obtenir un encadrement des solutions?
Le théorème des valeurs intermédiaires nous permet de prouver l'existence de solutions, mais il ne nous donne pas de valeurs approchées de ces solutions. Nous allons utiliser deux méthodes pour obtenir un encadrement des solutions:
Exemple: On cherche un encadrement à $10^{-2}$ de la solution de l'équation $x^3=-0,2$ : La fonction $f:x\longmapsto x^3$ est continue, strictement croissante sur $\mathbb{R}$, $f(-1)=-1$ et $f(0)=0$ d'où $f(-1) < -0,2 < f(0) $ donc d'après le théorème des valeurs intermédiaires l'équation $x^3=-0,2$ a une unique solution dans l'intervalle $\big] -1~;~0\big[$. On définit la fonction à l'aide de l'éditeur de fonctions: 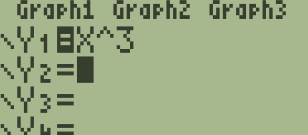
On initialise la table de la calculatrice : 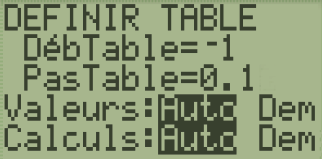
On consulte la table de la calculatrice : 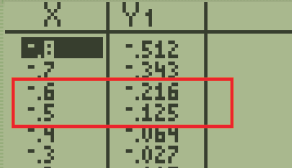
On en déduit que la solution se trouve entre -0,6 et -0,6 car $f(-0,6) < -0,2 < f(-0,5) $.
On recommence avec un pas de 0,01
On en déduit que la solution se trouve entre $-0,59$ et $-0,58$ car $f(-0,59) < -0,2 < f(-0,58) $.
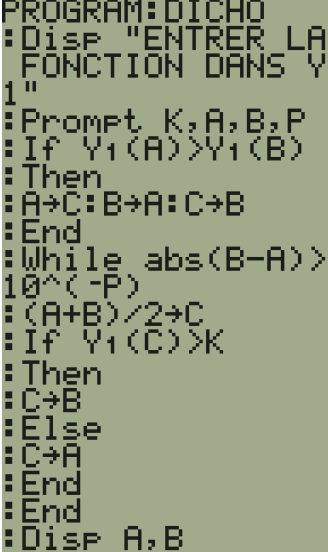
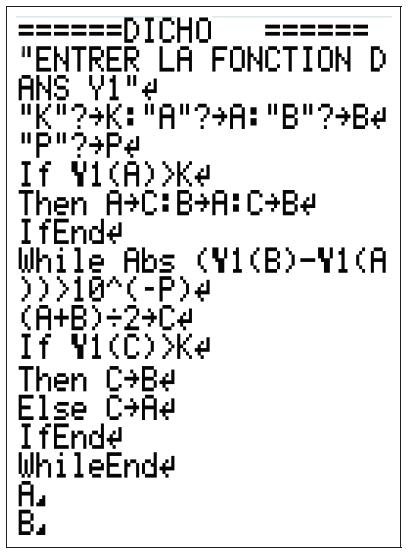
On utilise un algorithme que l'on peut programmer: 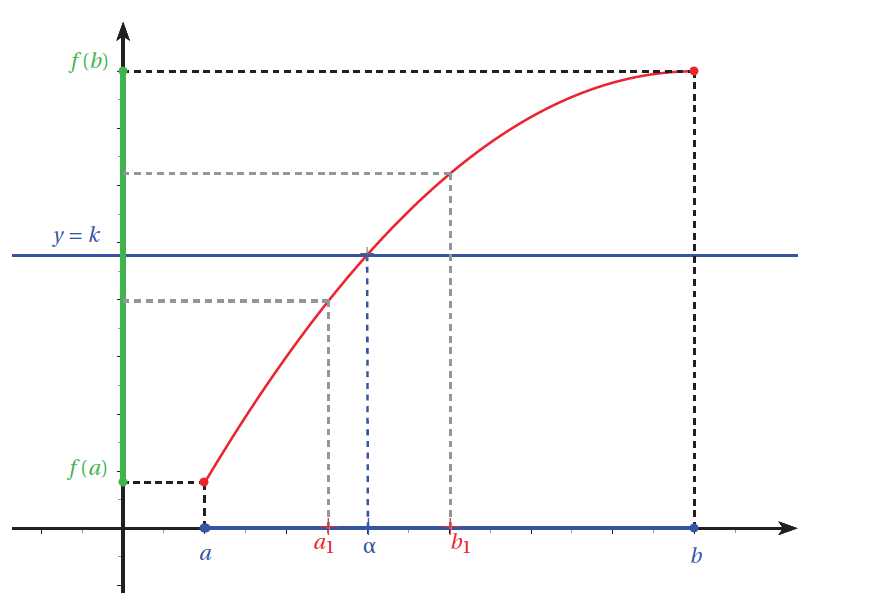
On cherche un encadrement à $10^{-p}$ de la solution de l'équation $f(x)=k$ sur un intervalle $\big[a~;~b\big]$ après s'être assuré que $k$ se trouve entre $f(a)$ et $f(b)$ : $$\begin{array}{|l|l|} \hline \text{Entrée}& \\ \text{Algorithme}& \text{Commentaires} \\ \hline \text{ Saisir } a text{ et } b & \text{ On entre les bornes de l'intervalle }\\ \text{ Saisir } k & \\ \text{ Saisir } p & \text{ On entre la précision }\\ & \\ \text{ Si } f(a)>k \text{ alors } & \\ c \text{ prend la valeur } a & \text{Si } f \text{ est décroissante }\\ a \text{ prend la valeur } b & \text{On permute les bornes de l'intervalle }\\ b \text{ prend la valeur } c & \\ \text{FinSi} & \\ \text{Tant que } \big|b-a \big|> 10^{-p}\qquad \qquad & \\ c \text{ prend la valeur } (a+b)/2 & \text{ On partage l'intervalle en deux }\\ \text{Si } f(c)< k \text{ alors } & \text{On détermine le nouvel intervalle} \\ a \text{ prend la valeur } c & \text{ contenant la solution}\\ \text{Sinon } & \\ b \text{ prend la valeur } c & \\ \text{Finsi } & \\ \text{FinTantQue } & \\ & \\ \text{ Afficher } a \text{ et } b & \text{ On affiche l encadrement }\\ \hline \end{array}$$ Voici le programme sur TI83 et sur Graph 85:
|
|
- Vues: 4317
