Baccalauréat STI2D Antilles-Guyane 18 juin 2014 - Exercice 3

Page 4 sur 4: Exercice 3

Exercice 3 7 points

Pavages

Les trois parties peuvent être traitées de manière indépendante

Partie A : observation du pavage

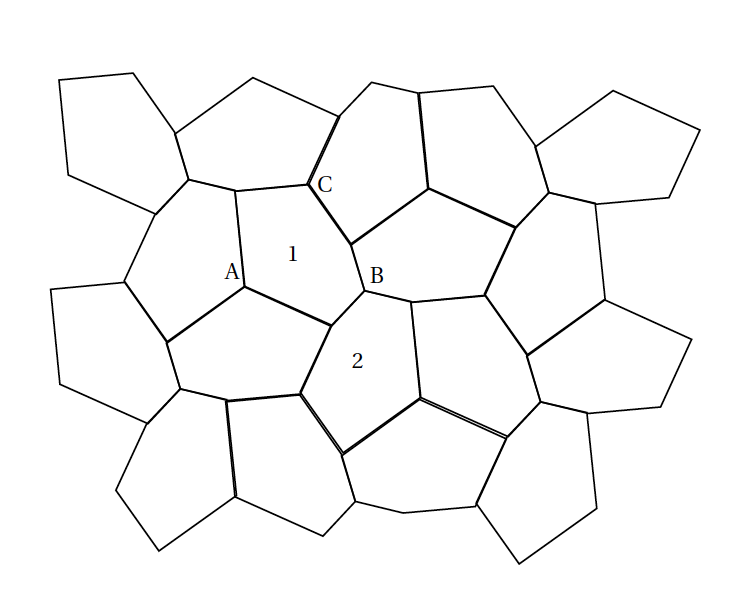
A l'aide d'un logiciel de géométrie dynamique, on a construit le pavage donné en annexe 2. Ce pavage est constitué d'hexagones identiques.

1. Quelle transformation permet de passer de l'hexagone 1 à l'hexagone 2. Préciser les caractéristiques de cette transformation.
2. Hachurer sur le pavage de l'annexe 2 tous les hexagones qui sont l'image de l'hexagone 1 par une translation.

Partie B : Obtention du motif

On considère un triangle équilatéral ABC de cà´té 5 cm et un point M situé à l'intérieur du triangle ABC tel que AM = 4 cm et BM = 2 cm.

Le point M$_{1}$ est l'image du point M par la symétrie axiale d'axe (AB).

Le point M$_{2}$ est l'image du point M par la symétrie axiale d'axe (BC).

Le point M$_{3}$ est l'image du point M par la symétrie axiale d'axe (AC).

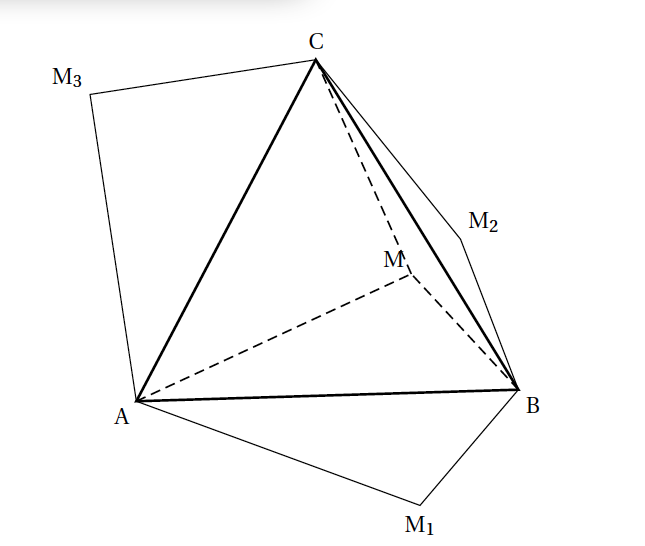
1. Justifier que l'hexagone AM$_{1}$BM$_{2}$CM$_{}$ a pour aire le double de l'aire du triangle ABC.
2. 1. En appliquant la formule d'Al-Kashi dans le triangle MAB, déterminer la valeur exacte du cosinus de l'angle $\widehat{\text{MAB}}$ puis la mesure approchée au dixième de degré de cet angle. En déduire la mesure approchée au dixième de degré de l'angle $\widehat{\text{MAC}}$.
   2. Dans cette question, on prendra 37,7 °{} comme mesure de l'angle $\widehat{\text{MAC}}$. Déterminer par le calcul une valeur approchée au centième de centimètre près de la longueur CM.

Partie C : Construction d'un pavage différent

L'objectif de cette partie est de construire un pavage différent.
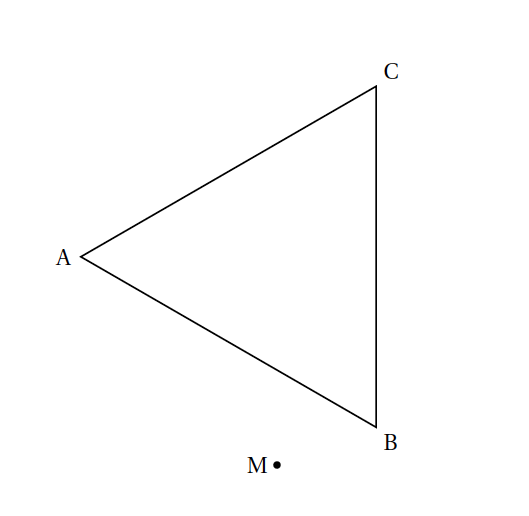
On place cette fois le point M à l'extérieur du triangle équilatéral.
Sur l'annexe 3, un triangle équilatéral ABC est tracé. M est un point extérieur au triangle.

1. Construire le symétrique M$_{1}$ de M par rapport à l'axe (AB), le symétrique M$_{2}$ de M par rapport à l'axe (BC), le symétrique M$_{3}$ de M par rapport à l'axe (AC). Tracer en couleur l'hexagone AM$_{1}$BM$_{2}$CM$_{3}$.
2. En utilisant des couleurs différentes, construire soigneusement l'image de cet hexagone par la rotation de centre A et d'angle 120 °, puis par la rotation de centre A et d'angle 240 °, le sens de rotation choisi étant le sens anti-horaire (le sens inverse des aiguilles d'une montre). Laisser les traits de construction apparents.

Annexe 1 - Exercice 1 (à rendre avec la copie)

Partie A

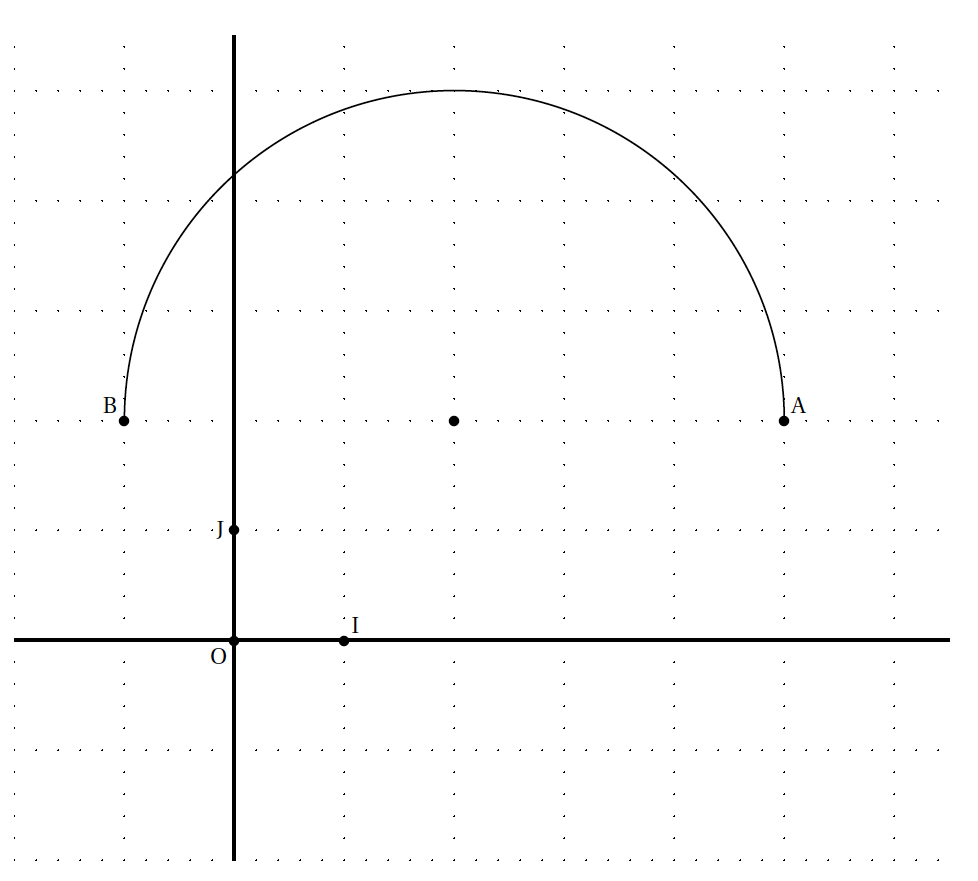
Partie B

$$\begin{array}{ |c|c|c|c|c|c|c|} \hline x&0&1&2&3&4&5\\ \hline f(x)&&&- 0,016 &&1,632&\\ \hline \end{array}$$

Annexe 2 - Exercice 3 (à rendre avec la copie)

Annexe 3 - Exercice 3 (à rendre avec la copie)