Baccalauréat STI 2D Métropole septembre 2013 - Correction Exercice 4
Page 8 sur 8
Exercice 4 6 points
Un architecte veut établir les plans d'un hangar pour ballon dirigeable. La forme de la façade avant de ce hangar et les points O, A, B, S, H et K sont donnés sur le schéma ci-dessous. 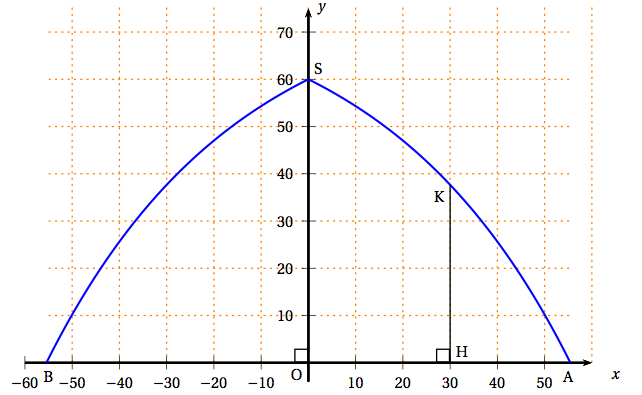
Cette façade avant est symétrique par rapport au segment vertical $[\mathrm{OS}]$ et $\mathrm{OH} = 30 \mathrm{m}$. L'arc $\overset{\displaystyle\frown}{SA}$ de la façade avant correspond à une partie de la représentation graphique d'une fonction définie sur l'intervalle $[0;60]$, dans un repère orthonormal direct d'origine O du plan, l'unité étant le mètre. Le cahier des charges impose les quatre conditions suivantes :
- $\mathrm{OS} = 60$ ;
- $\mathrm{HK} > 35$ ;
- la fonction évoquée ci-dessus doit être strictement décroissante sur l'intervalle [0;60] ;
- $\mathrm{OA} \leqslant 60$.
Partie A- Étude d'une fonction numérique
- Vérifier que la fonction $f$ définie sur l'intervalle $[0;60]$ par $f(x) = 80 - 20e^{0,025x}$ vérifie les trois premières conditions du cahier des charges. $\bullet~~$OS $ = f(0) = 80 - 20\text{e}^{0}= 80 - 20 = 60$.
- Déterminer, à l'aide de la calculatrice, la valeur décimale approchée à $10^{- 1}$ près par excès du réel $a$ qui vérifie $f(a) = 0$. Vérifier que la quatrième condition du cahier des charges est remplie. La calculatrice donne : $f(55) \approx 0,9 ; f(56) \approx -1$, donc $55 < a < 56$. $f(55,4) \approx 0,1$ et $f(55,5) \approx - 0,1$, donc $55,4 < a < 55,5$.
$\bullet~~$HK $ = f(30) = 80 - 20\text{e}^{0,025 \times 30} = 80 - 20\text{e}^{0,75} \approx 37,7 > 35$.
$\bullet~~$$f'(x) = - 20 \times 0,025 \text{e}^{0,025x} = - 0,5\text{e}^{0,025x}$. Comme $\text{e}^{0,025x} > 0$ quel que soit le réel $x$, $f'(x) < 0$ : la fonction $f$ est strictement décroissante sur $[0~;~60]$.
Partie B- Calcul d'intégrale et application
-
- La fonction $F$ est définie sur l'intervalle $[0;60]$ par $F(x) = 80x - 800e^{0,025x}$. Vérifier que la fonction $F$ est une primitive de la fonction $f$ sur l'intervalle $[0;60]$. On calcule sur $[0~;~60] F'(x) = 80 - 800 \times 0,025\text{e}^{0,025x} = 80 - 20\text{e}^{0,025x} = f(x)$ : $F$ est donc bien une primitive de $f$ sur l'intervalle [0~;~60].
- Calculer la valeur exacte de l'intégrale $J = \displaystyle\int_{0}^{55,5} f(x) \;d x$. $$\begin{array}{ll}J &= \displaystyle\int_{0}^{55,5} f(x)\:\text{d}x \\ &= \left[F(x) \right]_{0}^{55,5} \\&= F(55,5) - F(0)\\& = 80 \times 55,5 - 800\text{e}^{0,025 \times 55,5} - \left(80 \times 0 - 800\text{e}^{0,025\times 0} \right)\\& = 4440 - 800\text{e}^{ 1,3875 } + 800 = 5240 - 800\text{e}^{ 1,3875 } \end{array} $$
- Donner la valeur approchée, arrondie à $10^{- 2}$ près de $J$.
$\displaystyle\int_{0}^{55,5} f(x)\:\text{d}x = 5240 - 800\text{e}^{ 1,3875 }$ - On souhaite peindre la surface extérieure de la façade avant.
- Déterminer à $10^{-2}$ près l'aire de cette surface exprimée en $\mathrm{m}^2$. L'aire $\mathcal{A}$ de la surface à peindre est égale à :$\mathcal{A} = 2 J \approx 2 \times 2036,14 $, soit
- La peinture utilisée pour peindre la surface extérieure de la façade avant est vendue en bidons de 68 litres. Sachant que cette peinture a une propriété de recouvrement de 0,2 mètre carré par litre, combien de bidons sont nécessaires pour peindre la surface extérieure de la façade avant ? Un bidon permet de peindre $68 \times 0,2 = 13,6$ m$^2$. Pour peindre $ 4072,28 $ m$^2$ il faudra donc : $\dfrac{ 4072,28 }{13,6} \approx 299,4$.
$\mathcal{A} \approx 4072,28 $ m$^2$.Il faudra donc 300 bidons de peinture.
- Vues: 15517
