Baccalauréat S Liban 31 mai 2019 - Exercice 4
Page 7 sur 10
Exercice 4 5 points
Les deux parties 1 et 2 sont indépendantes.
Chaque semaine, un agriculteur propose en vente directe à chacun de ses clients un panier de produits frais qui contient une seule bouteille de jus de fruits. Dans un esprit de développement durable, il fait le choix de bouteilles en verre incassable et demande à ce que chaque semaine, le client rapporte sa bouteille vide. On suppose que le nombre de clients de l'agriculteur reste constant. Une étude statistique réalisée donne les résultats suivants :
- à l'issue de la première semaine, la probabilité qu'un client rapporte la bouteille de son panier est $0,9$;
- si le client a rapporté la bouteille de son panier une semaine, alors la probabilité qu'il ramène la bouteille du panier la semaine suivante est $0,95$ ;
- si le client n'a pas rapporté la bouteille de son panier une semaine, alors la probabilité qu'il ramène la bouteille du panier la semaine suivante est $0,2$.
On choisit au hasard un client parmi la clientèle de l'agriculteur. Pour tout entier naturel $n$ non nul, on note $R_n$ l'évènement « le client rapporte la bouteille de son panier de la $n$-ième semaine ».
-
- Modéliser la situation étudiée pour les deux premières semaines à l'aide d'un arbre pondéré qui fera intervenir les évènements $R_1$ et $R_2$.
- Déterminer la probabilité que le client rapporte ses bouteilles des paniers de la première et de la deuxième semaine.
- Montrer que la probabilité que le client rapporte la bouteille du panier de la deuxième semaine est égale à $0,875$.
- Sachant que le client a rapporté la bouteille de son panier de la deuxième semaine, quelle est la probabilité qu'il n'ait pas rapporté la bouteille de son panier de la première semaine ? On arrondira le résultat à $10^{-3}$.
- Pour tout entier naturel $n$ non nul, on note $r_n$ la probabilité que le client rapporte la bouteille du panier de la $n$-ième semaine. On a alors $r_n = p\left(R_n\right)$.
- Recopier et compléter l'arbre pondéré (aucune justification n'est attendue) :
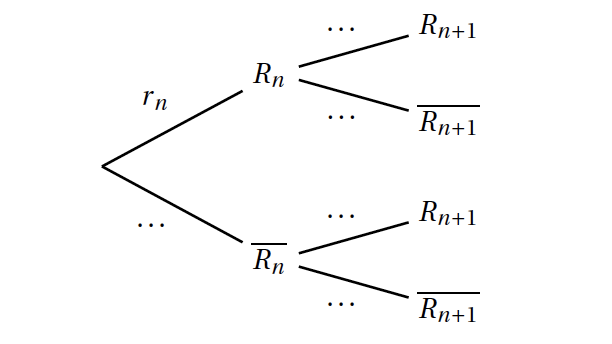
- Justifier que pour tout entier naturel $n$ non nul, $r_{n+1} = 0,75 r_n + 0,2$.
- Démontrer que pour tout entier naturel $n$ non nul, $r_n = 0,1 \times 0,75^{n-1} + 0,8$.
- Calculer la limite de la suite $\left(r_n\right)$. Interpréter le résultat dans le contexte de l'exercice.
- Recopier et compléter l'arbre pondéré (aucune justification n'est attendue) :
- Vues: 58211
