Baccalauréat S Polynésie 13 juin 2014
Exercice 1 5 points
Dans un repère orthonormé de l'espace, on considère les points \[\text{A}(5~;~-5~;~2), \text{B} (-1~;~1~;~0), \text{C}(0~;~1~;~2)\quad \text{et D}(6~;~6~;~-1).\]
- Déterminer la nature du triangle BCD et calculer son aire.
-
- Montrer que le vecteur $\vec{n}\begin{pmatrix}- 2\\3\\1\end{pmatrix}$ est un vecteur normal au plan (BCD).
- Déterminer une équation cartésienne du plan (BCD).
- Déterminer une représentation paramétrique de la droite $\mathcal{D}$ orthogonale au plan (BCD) et passant par le point A.
- Déterminer les coordonnées du point $H$, intersection de la droite $\mathcal{D}$ et du plan $(BCD)$.
- Déterminer les coordonnées du point H, intersection de la droite $\mathcal{D}$ et du plan (BCD).
- Déterminer le volume du tétraèdre ABCD. On rappelle que le volume d'un tétraèdre est donné par la formule $\mathcal{V} = \dfrac{1}{3}\mathcal{B} \times h$, où $\mathcal{B}$ est l'aire d'une base du tétraèdre et $h$ la hauteur correspondante.
- On admet que AB = $\sqrt{76}$ et AC $= \sqrt{61}$. Déterminer une valeur approchée au dixième de degré près de l'angle $\widehat{\text{BAC}}$.
Correction de l'exercice 1 (5 points)
- Déterminer la nature du triangle BCD et calculer son aire.
-
- Montrer que le vecteur $\vec{n}\begin{pmatrix}- 2\\3\\1\end{pmatrix}$ est un vecteur normal au plan (BCD). Le vecteur $\overrightarrow{n}\begin{pmatrix}- 2\\3\\1\end{pmatrix}$ est un vecteur normal au plan $(BCD)$: $$ \overrightarrow{BC}\begin{pmatrix}1\\0\\2\end{pmatrix}\cdot\overrightarrow{n}\begin{pmatrix}- 2\\3\\1\end{pmatrix}=1\times (-2)+0\times 3+2\times 1=0\ \text{et}\ \overrightarrow{CD}\begin{pmatrix}6\\5\\-3\end{pmatrix}\cdot\overrightarrow{n}\begin{pmatrix}- 2\\3\\1\end{pmatrix}=6\times (-2)+5\times 3+(-3)\times 1=0 $$ Comme $\overrightarrow{BC}$ et $\overrightarrow{CD}$ ne sont pas colinéaires ($BCD$ est un triangle rectangle non aplati), $\overrightarrow{n}$ étant orthogonal à deux vecteurs non colinéaires du plan $(BCD)$, il en est un vecteur normal.
- Déterminer une équation cartésienne du plan (BCD).
- L'équation est de la forme $-2x+3y+z+d=0$;
- $B$ appartient au plan, donc $-2(-1)+3(1)+(0)+d=0\Longleftrightarrow d=-5$;
- une équation cartésienne du plan $(BCD)$ est: $-2x+3y+z-5=0$.
- Déterminer une représentation paramétrique de la droite $\mathcal{D}$ orthogonale au plan (BCD) et passant par le point A.
- Déterminer les coordonnées du point H, intersection de la droite $\mathcal{D}$ et du plan (BCD).
$$ \left\lbrace\begin{array}{l} x = 5-2t\\ y = -5+3t\\ z =2+t\\ -2x+3y+z-5=0 \end{array}\right.\Longleftrightarrow \left\lbrace\begin{array}{l} x = 5-2t\\ y = -5+3t\\ z =2+t\\ -2(5-2t)+3(-5+3t)+(2+t)-5=0 \end{array}\right.\Longleftrightarrow \left\lbrace\begin{array}{l} x = 5-2(2)=1\\ y = -5+3(2)=1\\ z =2+2=4\\ t=2 \end{array}\right. $$ Ainsi, les coordonnées de $H$ sont: $(1;1;4)$. - Déterminer le volume du tétraèdre ABCD. On rappelle que le volume d'un tétraèdre est donné par la formule $\mathcal{V} = \dfrac{1}{3}\mathcal{B} \times h$, où $\mathcal{B}$ est l'aire d'une base du tétraèdre et $h$ la hauteur correspondante.
- On admet que AB = $\sqrt{76}$ et AC $= \sqrt{61}$. Déterminer une valeur approchée au dixième de degré près de l'angle $\widehat{\text{BAC}}$.
$$\left\lbrace\begin{array}{l} BC^2 = (0-(-1))^2+(1-1)^2+(2-0)^2=5\\ CD^2 = (6-0)^2+(6-1)^2+(-1-2)^2=70\\ BD^2 = (6-(-1))^2+(6-1)^2+(-1-0)^2=75 \end{array}\right.\Longrightarrow BD^2=BC^2+CD^2\Longrightarrow BCD \text{est rectangle en} C $$ Son aire est: $\dfrac{BC\times CD}{2}=\dfrac{\sqrt{5}\times \sqrt{70}}{2}=5\sqrt{7}$.
$\mathcal{A}(BCD)=5\sqrt{7}$.
(donc de vecteur directeur $\overrightarrow{n}$) et passant par le point $A$: $$ \left\lbrace\begin{array}{l} x=5-2t\\ y=-5+3t\\ z=2+t \end{array}\right.\ \text{avec}\ t\in\mathbb{R} $$
$[AH]$ est la hauteur du tétraèdre, car $A$ est sur la droite $\mathcal{D}$ orthogonale au plan $(BCD)$ et $H$ est l'intersection de $\mathcal{D}$ et $(BCD)$, donc la projection orthogonale de $A$ sur $(BCD)$. $\mathcal{B}=5\sqrt{7}$; $h=AH=\sqrt{(5-1)^2+(-5-1)^2+(2-4)^2}=4\sqrt{14}$; donc: $$ \mathcal{V} = \frac{1}{3}\mathcal{B} \times h=\frac{1}{3}\times 4\sqrt{14}\times 5\sqrt{7}=\frac{1}{3}140\sqrt{2} $$ $ \mathcal{V} =\frac{1}{3}140\sqrt{2} $
\[ \overrightarrow{AB}\begin{pmatrix}-6\\6\\-2\end{pmatrix};\ AB=\sqrt{(-6)^2+6^2+(-2)^2}=\sqrt{76};\ \overrightarrow{AC}\begin{pmatrix}-5\\6\\0\end{pmatrix};\ AB=\sqrt{(-5)^2+6^2+(0)^2}=\sqrt{61}; \] \[ \cos\widehat{BAC}=\frac{\overrightarrow{AB}.\overrightarrow{AC}}{AB\times AC} =\frac{(-6)\times(-5)+6\times 6+(-2)\times 0}{\sqrt{76}\times \sqrt{61}}=\frac{66}{\sqrt{4 636}}\simeq 0,97\Longrightarrow \text{mes}\widehat{BAC}\simeq 14,2\ \text{au dixième de degré près} \] $ \text{mes}\widehat{BAC}\simeq 14,2^{\circ} \text{au dixième de degré près} $
Exercice 2 5 points
Soient $f$ et $g$ les fonctions définies sur $\mathbb{R}$ par \[f(x) = \text{e}^x \quad \text{et} \quad g(x) = 2\text{e}^{\frac{x}{2}} - 1.\] On note $\mathcal{C}_{f}$ et $\mathcal{C}_{g}$ les courbes représentatives des fonctions $f$ et $g$ dans un repère orthogonal.
- Démontrer que les courbes $\mathcal{C}_{f}$ et $\mathcal{C}_{g}$ ont un point commun d'abscisse $0$ et qu'en ce point, elles ont la même tangente $\Delta$ dont on déterminera une équation.
- Étude de la position relative de la courbe $\mathcal{C}_{g}$ et de la droite $\Delta$ Soit $h$ la fonction définie sur $\mathbb{R}$ par $h(x) = 2\text{e}^{\frac{x}{2}} - x - 2$.
- Déterminer la limite de la fonction $h$ en $- \infty$.
- Justifier que, pour tout réel $x, h(x) = x\left(\dfrac{\text{e}^{\frac{x}{2}}}{\frac{x}{2}} - 1 - \dfrac{2}{x}\right)$. En déduire la limite de la fonction $h$ en $+ \infty$.
- On note $h'$ la fonction dérivée de la fonction $h$ sur $\mathbb{R}$. Pour tout réel $x$, calculer $h'(x)$ et étudier le signe de $h'(x)$ suivant les valeurs de $x$.
- Dresser le tableau de variations de la fonction $h$ sur $\mathbb{R}$.
- En déduire que, pour tout réel $x,\:\: 2\text{e}^{\frac{x}{2}} - 1 \geqslant x + 1$.
- Que peut-on en déduire quant à la position relative de la courbe $\mathcal{C}_{g}$ et de la droite $\Delta$ ?
- Étude de la position relative des courbes $\mathcal{C}_{f}$ et $\mathcal{C}_{g}$
- Pour tout réel $x$, développer l'expression $\left(\text{e}^{\frac{x}{2}} - 1\right)^2$.
- Déterminer la position relative des courbes $\mathcal{C}_{f}$ et $\mathcal{C}_{g}$.
- Calculer, en unité d'aire, l'aire du domaine compris entre les courbes $\mathcal{C}_{f}$ et $\mathcal{C}_{g}$ et les droites d'équations respectives $x = 0$ et $x = 1$.
Correction de l'exercice 2 (5 points)
- Démontrer que les courbes $\mathcal{C}_{f}$ et $\mathcal{C}_{g}$ ont un point commun d'abscisse $0$ et qu'en ce point, elles ont la même tangente $\Delta$ dont on déterminera une équation.
- Étude de la position relative de la courbe $\mathcal{C}_{g}$ et de la droite $\Delta$ Soit $h$ la fonction définie sur $\mathbb{R}$ par $h(x) = 2\text{e}^{\frac{x}{2}} - x - 2$.
- Déterminer la limite de la fonction $h$ en $- \infty$.
- Justifier que, pour tout réel $x, h(x) = x\left(\dfrac{\text{e}^{\frac{x}{2}}}{\frac{x}{2}} - 1 - \dfrac{2}{x}\right)$. En déduire la limite de la fonction $h$ en $+ \infty$.
- On note $h'$ la fonction dérivée de la fonction $h$ sur $\mathbb{R}$. Pour tout réel $x$, calculer $h'(x)$ et étudier le signe de $h'(x)$ suivant les valeurs de $x$.
- Dresser le tableau de variations de la fonction $h$ sur $\mathbb{R}$.
Limite de la fonction $h$ en $- \infty$: $$ \lim_{x\to-\infty}h(x)=\lim_{x\to-\infty}(-x)=+\infty\ \text{car}\ \lim_{x\to-\infty}\text{e}^{\frac{x}{2}}=0 $$
Pour tout réel $x$ $$ x\left(\frac{\text{e}^{\frac{x}{2}}}{\frac{x}{2}}-1-\dfrac{2}{x}\right)={x}\times\text{e}^{\frac{x}{2}}\times \frac{2}{{x}}-x-{x}\frac{2}{{x}}=2\text{e}^{\frac{x}{2}} - x - 2=h(x) $$ Limite de la fonction $h$ en $+ \infty$: $$ \lim_{x\to+\infty}h(x)=\lim_{x\to+\infty}x\times \frac{\text{e}^{\frac{x}{2}}}{\frac{x}{2}}=+\infty,\ \text{car}\ \lim_{x\to+\infty}\frac{2}{x}=0\ \text{et}\ \lim_{X=\frac{x}{2}\to+\infty}\frac{\text{e}^X}{X}=+\infty $$
$$ h'(x)=2\times\frac{1}{2}\text{e}^{\frac{x}{2}}-1=\text{e}^{\frac{x}{2}}-1 $$ $$h'(x)>0\Longleftrightarrow \text{e}^{\frac{x}{2}}>1 \Longleftrightarrow \frac{x}{2}>0\Longleftrightarrow x>0$$ - En déduire que, pour tout réel $x,\:\: 2\text{e}^{\frac{x}{2}} - 1 \geqslant x + 1$.
- Que peut-on en déduire quant à la position relative de la courbe $\mathcal{C}_{g}$ et de la droite $\Delta$ ?
$$ M(x;y)\in \mathcal{C}_{f}\cap \mathcal{C}_{g}\Longleftrightarrow f(x)=g(x)\Longleftrightarrow \text{e}^x=2\text{e}^{\frac{x}{2}}-1\Longleftrightarrow \left\lbrace\begin{array}{l} X=\text{e}^{\frac{x}{2}}\\ X^2-2X+1=(X-1)^2=0 \end{array}\right.\Longleftrightarrow \text{e}^{\frac{x}{2}}=1\Longleftrightarrow x=0 $$ Ainsi $M$ a pour coordonnées $(0\,;\,1)$. $$ f'(x)=\text{e}^x\Longrightarrow f'(0)=1\quad;\quad g'(x)=\text{e}^{\frac{x}{2}}\Longrightarrow g'(0)=1 $$ En $M$, leurs tangentes ont, toutes deux le même coefficient directeur $1$, elles ont donc même tangente $\Delta$ d'équation $y-1=1(x-0)\Longleftrightarrow y=x+1$.
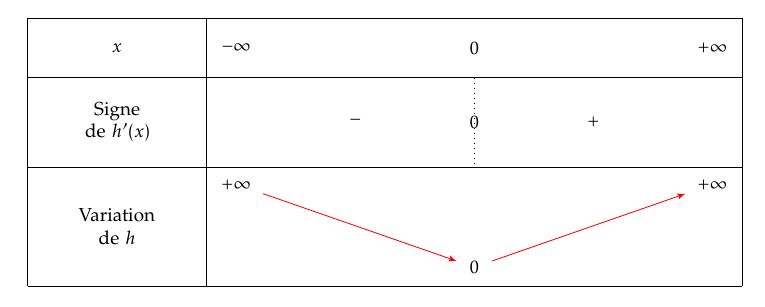
La fonction $h$ possède un minimum en $0$ qui est $0$. Donc: $$ \forall x,\ x\in\mathbb{R},\ h(x)\geqslant 0\Longleftrightarrow 2\text{e}^{\frac{x}{2}}-x-2=2\text{e}^{\frac{x}{2}}-1-x-1\geqslant 0\Longleftrightarrow 2\text{e}^{\frac{x}{2}}-1\geqslant x+1 $$
Ainsi la courbe $\mathcal{C}_{g}$ se trouve au dessus de la droite d'équation $y=x+1$ qui est la droite $\Delta$.
- Pour tout réel $x$, développer l'expression $\left(\text{e}^{\frac{x}{2}} - 1\right)^2$.
- Déterminer la position relative des courbes $\mathcal{C}_{f}$ et $\mathcal{C}_{g}$.
On a vu plus haut (question 1.) que, pour tout réel $x$, $\left(\text{e}^{\frac{x}{2}}-1\right)^2=f(x)-g(x)\geqslant 0$.
Ainsi la courbe $\mathcal{C}_{f}$ se trouve au dessus de la courbe $\mathcal{C}_{g}$. Ainsi, $\left|f(x)- g(x)\right| = \left(f(x) - g(x)\right)$.
$$\begin{array}{cc} \mathcal{A}&=\int_0^1\left|f(x)-g(x)\right|\text{d}x=\int_0^1\left(f(x)-g(x)\right)\text{d}x=\int_0^1\text{e}^x\text{d}x-4\int_0^1\frac{1}{2}\text{e}^{\frac{x}{2}}\text{d}x+\int_0^1\text{d}x\\ &= \left\lbrack\text{e}^x\right\rbrack_0^1-4\left\lbrack\text{e}^{\frac{x}{2}}\right\rbrack_0^1+\left\lbrack x\right\rbrack_0^1=\text{e}-1-4\text{e}^{\frac{1}{2}}+4+1=\text{e}-4\sqrt{\text{e}}+4\simeq 0,123\\ \end{array}$$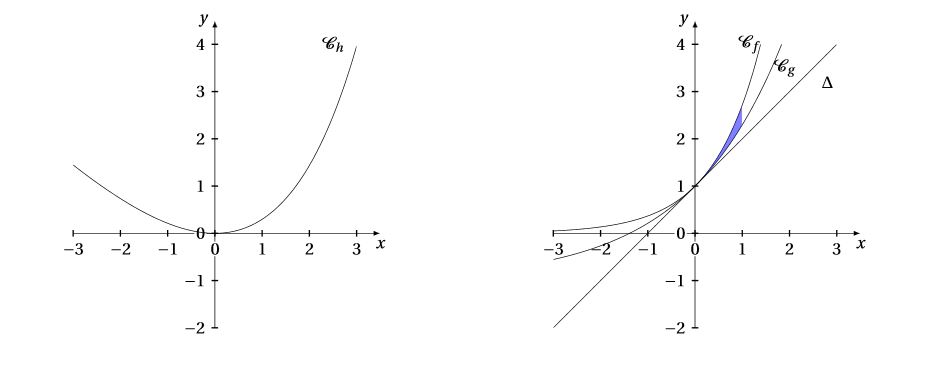
Exercice 3 5 points
Pour chacune des cinq affirmations suivantes, indiquer si elle est vraie ou fausse et justifier la réponse. Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.
- Zoé se rend à son travail à pied ou en voiture. Là où elle habite, il pleut un jour sur quatre.Lorsqu'il pleut, Zoé se rend en voiture à son travail dans 80 % des cas. Lorsqu'il ne pleut pas, elle se rend à pied à son travail avec une probabilité égale à $0,6$.
- Dans l'ensemble $E$ des issues d'une expérience aléatoire, on considère deux évènements $A$ et $B$.
Affirmation n° 2 : « Si $A$ et $B$ sont indépendants, alors $A$ et $\overline{B}$ sont aussi indépendants. »
- On modélise le temps d'attente, exprimé en minutes, à un guichet, par une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $0,7$. Affirmation n° 3 :
- On sait que 39 % de la population française est du groupe sanguin A+. On cherche à savoir si cette proportion est la même parmi les donneurs de sang. On interroge $183$ donneurs de sang et parmi eux, 34 % sont du groupe sanguin A+.
Affirmation n° 5 :
« On ne peut pas rejeter, au seuil de 5 %, l'hypothèse selon laquelle la proportion de personnes du groupe sanguin A+ parmi les donneurs de sang est de 39 % comme dans l'ensemble de la population. »
Affirmation n° 1 :
« Zoé utilise la voiture un jour sur deux. »
« La probabilité qu'un client attende au moins cinq minutes à ce guichet est $0,7$ environ. »
Affirmation n° 4 :
« Le temps d'attente moyen à ce guichet est de sept minutes.»
Correction de l'exercice 3 (5 points)
- Zoé se rend à son travail à pied ou en voiture. Là où elle habite, il pleut un jour sur quatre.Lorsqu'il pleut, Zoé se rend en voiture à son travail dans 80 % des cas. Lorsqu'il ne pleut pas, elle se rend à pied à son travail avec une probabilité égale à $0,6$.
- Dans l'ensemble $E$ des issues d'une expérience aléatoire, on considère deux évènements $A$ et $B$.
Affirmation n° 2 :« Si $A$ et $B$ sont indépendants, alors $A$ et $\overline{B}$ sont aussi indépendants. » - On modélise le temps d'attente, exprimé en minutes, à un guichet, par une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $0,7$. Affirmation n° 3 :
- On sait que 39 % de la population française est du groupe sanguin A+. On cherche à savoir si cette proportion est la même parmi les donneurs de sang. On interroge $183$ donneurs de sang et parmi eux, 34 % sont du groupe sanguin A+.
Affirmation n° 5 :
« On ne peut pas rejeter, au seuil de 5 %, l'hypothèse selon laquelle la proportion de personnes du groupe sanguin A+ parmi les donneurs de sang est de 39 % comme dans l'ensemble de la population. »
Affirmation n° 1 :
« Zoé utilise la voiture un jour sur deux. »
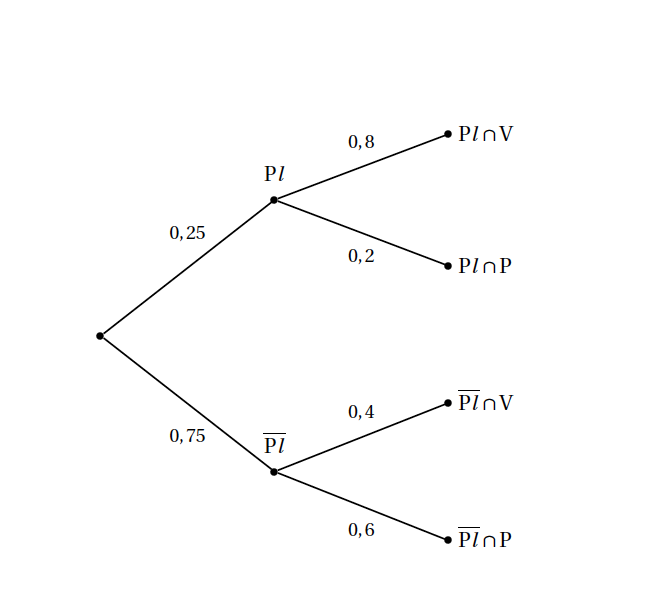
Pl: il pleut; V: en voiture; P: à pied
On cherche $p(V)$: $$\begin{array} p(V)&=p(V\cap \text{Pl})+p(V\cap \overline{\text{Pl}})\\ &=p_{\text{Pl}}(V)\times p(\text{Pl})+p_{\overline{\text{Pl}}}(V)\times p(\overline{\text{Pl}})\\ &= 0,8\times 0,25+0,4\times 0,75=0,5 \end{array}$$
« Zoé utilise la voiture un jour sur deux. »
Affirmation no 1 : VRAIE
Dans l'ensemble $E$ des issues d'une expérience aléatoire, on considère deux événements $A$ et $B$. $A$ et $B$ sont indépendants signifie que $p(A\cap B)=p(A)\times p(B)$: \[ p(A)=p(A\cap B)+p(A\cap\overline{B})=p(A)\times p(B)+p(A\cap\overline{B})\Longrightarrow p(A\cap\overline{B})=p(A)-p(A)\times p(B)=p(A)\left(1-p(B)\right)=p(A)\times p(\overline{B}) \]
« Si $A$ et $B$ sont indépendants, alors $A$ et $\overline{B}$ sont aussi indépendants. »
Affirmation no 2 : VRAIE
« La probabilité qu'un client attende au moins cinq minutes à ce guichet est $0,7$ environ. »
On modélise le temps d'attente, exprimé en minutes, à un guichet, par une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $0,7$. Affirmation no 3 : FAUX $$ p(X<5)=\int_0^5 -0,7\text{e}^{-0,7x}\text{d}x=\left\lbrack-\text{e}^{-0,7x}\right\rbrack_0^5 =1-\text{e}^{-0,7\times 5}\approx 0,503 $$ « La probabilité qu'un client attende au moins cinq minutes à ce guichet est $0,503$ environ. » Affirmation n° 4 :
« Le temps d'attente moyen à ce guichet est de sept minutes.»
Affirmation no 4 : FAUX $$ E(X)=\frac{1}{\lambda}=\frac{1}{0,7}\simeq 1,42 $$ « Le temps d'attente moyen à ce guichet est d'environ 1 minute et demi.»
On sait que 39 % de la population française est du groupe sanguin A+ ($p=0,39$). On cherche à savoir si cette proportion est la même parmi les donneurs de sang. On interroge $n=183$ donneurs de sang et parmi eux, 34 % sont du groupe sanguin A+ ($f=0,34$). On va trouver un intervalle de confiance au seuil de 95 %. $$\left\lbrack f-\frac{1}{\sqrt{n}}\,;\,f+\frac{1}{\sqrt{n}}\right\rbrack= \left\lbrack 0,34-\frac{1}{\sqrt{183}}\,;\,0,34+\frac{1}{\sqrt{183}}\right\rbrack\subset \left\lbrack 0,26~;~0,42\right\rbrack\ni p=0,39 $$ « On ne peut donc pas rejeter, au seuil de 5 %, l'hypothèse selon laquelle la proportion de personnes du groupe sanguin A+ parmi les donneurs de sang est de 39 % comme dans l'ensemble de la population. »
Affirmation no 5 : VRAIE
Exercice 4 5 points
On considère la suite $\left(u_{n}\right)$ définie par \[u_{0} = 0\quad \text{et, pour tout entier naturel }\:n, u_{n+1} = u_{n} + 2n +2.\]
- Calculer $u_{1}$ et $u_{2}$.
- On considère les deux algorithmes suivants : $$\begin{array}{|l |l |l |l |l|}\hline \text{Algorithme 1}& & &\text{Algorithme 2}&\\ \hline \text{Variables :}& n \text{ est un entier naturel}& &\text{Variables :}& n \text{ est un entier naturel}\\ &u \text{ est un réel }& & &u \text{ est un réel } \\ \text{Entrée :}&\text{Saisir la valeur de } n &&\text{Entrée :}&\text{ Saisir la valeur de } n\\ \text{Traitement :}& u \text{ prend la valeur 0 }& &\text{Traitement :}& u \text{ prend la valeur 0}\\ &\text{ Pour } i \text{ allant de 1 à } n: & & &\text{ Pour } i \text{ allant de 1 à } n - 1 :\\ & u \text{ prend la valeur } u + 2i + 2& & & u \text{ prend la valeur } u + 2i + 2\\ &\text{ Fin Pour }& & &\text{ Fin Pour }\\ \text{Sortie :}& \text{ Afficher } u& &\text{Sortie :}& \text{Afficher } u\\ \hline \end{array}$$ De ces deux algorithmes, lequel permet d'afficher en sortie la valeur de $u_{n}$, la valeur de l'entier naturel $n$ étant entrée par l'utilisateur ?
- À l'aide de l'algorithme, on a obtenu le tableau et le nuage de points ci-dessous où $n$ figure en abscisse et $u_{n}$ en ordonnée.
$$\begin{array}{|c|c|}\hline n &u_{n}\\ \hline 0& 0 \\ \hline 1& 2 \\ \hline 2& 6 \\ \hline 3& 12 \\ \hline 4& 20 \\ \hline 5& 30 \\ \hline 6& 42 \\ \hline 7& 56 \\ \hline 8& 72 \\ \hline 9& 90 \\ \hline 10& 110\\ \hline 11& 132\\ \hline 12& 156\\ \hline \end{array}$$ 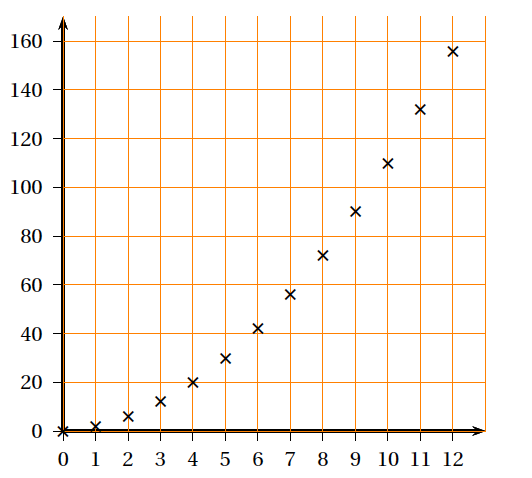
- Quelle conjecture peut-on faire quant au sens de variation de la suite $\left(u_{n}\right)$ ? Démontrer cette conjecture.
- La forme parabolique du nuage de points amène à conjecturer l'existence de trois réels $a, b$ et $c$ tels que, pour tout entier naturel $n$, $u_{n} = an^2 + bn + c$. Dans le cadre de cette conjecture, trouver les valeurs de $a, b$ et $c$ à l'aide des informations fournies.
- On définit, pour tout entier naturel $n$, la suite $\left(v_{n}\right)$ par : $v_{n} = u_{n+1} - u_{n}$.
- Exprimer $v_{n}$ en fonction de l'entier naturel $n$. Quelle est la nature de la suite $\left(v_{n}\right)$ ?
- On définit, pour tout entier naturel $n, S_{n} = \displaystyle\sum_{k=0}^{n} v_{k} = v_{0} + v_{1} + \cdots + v_{n}$. Démontrer que, pour tout entier naturel $n,S_{n} = (n + 1)(n + 2)$.
- Démontrer que, pour tout entier naturel $n, S_{n} = u_{n+1} - u_{0}$, puis exprimer $u_{n}$ en fonction de $n$.
Correction de l'exercice 4 (5 points)
- Calculer $u_{1}$ et $u_{2}$.
- On considère les deux algorithmes suivants : $$\begin{array}{|l |l |l |l |l|}\hline \text{Algorithme 1}& & &\text{Algorithme 2}&\\ \hline \text{Variables :}& n \text{ est un entier naturel}& &\text{Variables :}& n \text{ est un entier naturel}\\ &u \text{ est un réel }& & &u \text{ est un réel } \\ \text{Entrée :}&\text{Saisir la valeur de } n &&\text{Entrée :}&\text{ Saisir la valeur de } n\\ \text{Traitement :}& u \text{ prend la valeur 0 }& &\text{Traitement :}& u \text{ prend la valeur 0}\\ &\text{ Pour } i \text{ allant de 1 à } n: & & &\text{ Pour } i \text{ allant de 1 à } n - 1 :\\ & u \text{ prend la valeur } u + 2i + 2& & & u \text{ prend la valeur } u + 2i + 2\\ &\text{ Fin Pour }& & &\text{ Fin Pour }\\ \text{Sortie :}& \text{ Afficher } u& &\text{Sortie :}& \text{Afficher } u\\ \hline \end{array}$$ De ces deux algorithmes, lequel permet d'afficher en sortie la valeur de $u_{n}$, la valeur de l'entier naturel $n$ étant entrée par l'utilisateur ?
- À l'aide de l'algorithme, on a obtenu le tableau et le nuage de points ci-dessous où $n$ figure en abscisse et $u_{n}$ en ordonnée.
$$\begin{array}{|c|c|}\hline n &u_{n}\\ \hline 0& 0 \\ \hline 1& 2 \\ \hline 2& 6 \\ \hline 3& 12 \\ \hline 4& 20 \\ \hline 5& 30 \\ \hline 6& 42 \\ \hline 7& 56 \\ \hline 8& 72 \\ \hline 9& 90 \\ \hline 10& 110\\ \hline 11& 132\\ \hline 12& 156\\ \hline \end{array}$$ 
- Quelle conjecture peut-on faire quant au sens de variation de la suite $\left(u_{n}\right)$ ? Démontrer cette conjecture.
- La forme parabolique du nuage de points amène à conjecturer l'existence de trois réels $a, b$ et $c$ tels que, pour tout entier naturel $n$, $u_{n} = an^2 + bn + c$. Dans le cadre de cette conjecture, trouver les valeurs de $a, b$ et $c$ à l'aide des informations fournies.
La suite $\left(u_{n}\right)$ semble être croissante.
Démonstration : \[ u_{n+1}-u_n=u_{n} + 2n +2-u_n=2n+2>0\ \text{pour tout}n \text{naturel} \] - On définit, pour tout entier naturel $n$, la suite $\left(v_{n}\right)$ par : $v_{n} = u_{n+1} - u_{n}$.
- Exprimer $v_{n}$ en fonction de l'entier naturel $n$. Quelle est la nature de la suite $\left(v_{n}\right)$ ?
- On définit, pour tout entier naturel $n,\: S_{n} = \displaystyle\sum_{k=0}^{n} v_{k} = v_{0} + v_{1} + \cdots + v_{n}$. Démontrer que, pour tout entier naturel $n,\: S_{n} = (n + 1)(n + 2)$.
- Démontrer que, pour tout entier naturel $n,\: S_{n} = u_{n+1} - u_{0}$, puis exprimer $u_{n}$ en fonction de $n$.
C'est une suite arithmétique de raison $r=2$ et de premier terme $v_0=2$.
\[ S_n=\sum_{k=0}^{n} v_{k} = v_{0} + v_{1} + \cdots + v_{n}=(n+1)v_0+\frac{n(n+1)}{2}\times r=2(n+1)+n(n+1)=(n+1)(n+2) \] \[ S_n=({u_1}-u_0)+({u_2}-{u_1})+\cdots + ({u_n}-{u_{n-1}})+(u_{n+1}-{u_n})=u_{n+1}-u_0 \] \[ S_{n-1}=u_n-u_0\Longleftrightarrow u_n=S_{n-1}+u_0=n(n+1)+0=n(n+1) \]
$u_{1}=u_0=2\times 0+2=2$ et $u_{2}=u_1+2\times 1+2=6$.
Le second affiche en sortie la valeur de $u_{n}$, la valeur de l'entier naturel $n$ étant entrée par l'utilisateur.
\[ \left\lbrace\begin{array}{l} u_0=a\times 0^2+b\times 0+c=0\\ u_1=a\times 1^2+b\times 1+c=2\\ u_2=a\times 2^2+b\times 2+c=6 \end{array}\right.\Longleftrightarrow \left\lbrace\begin{array}{l} a+b=2\\ 4a+2b=6\\ c=0 \end{array}\right.\Longleftrightarrow \left\lbrace\begin{array}{l} a+b=2\\ 2a+b=3\\ c=0 \end{array}\right.\Longleftrightarrow \left\lbrace\begin{array}{l} a=1\\ b=1\\ c=0 \end{array}\right. \]
Spécialité 5 points
Dans cet exercice, on appelle numéro du jour de naissance le rang de ce jour dans le mois et numéro du mois de naissance, le rang du mois dans l'année.
Par exemple, pour une personne née le 14 mai, le numéro du jour de naissance est 14 et le numéro du mois de naissance est 5.
Partie A
Lors d'une représentation, un magicien demande aux spectateurs d'effectuer le programme de calcul (A) suivant : « Prenez le numéro de votre jour de naissance et multipliez-le par 12. Prenez le numéro de votre mois de naissance et multipliez-le par 37. Ajoutez les deux nombres obtenus. Je pourrai alors vous donner la date de votre anniversaire » . Un spectateur annonce $308$ et en quelques secondes, le magicien déclare : « Votre anniversaire tombe le 1er août ! » .
- Vérifier que pour une personne née le 1er août, le programme de calcul (A) donne effectivement le nombre $308$.
-
- Pour un spectateur donné, on note $j$ le numéro de son jour de naissance, $m$ celui de son mois de naissance et $z$ le résultat obtenu en appliquant le programme de calcul (A). Exprimer $z$ en fonction de $j$ et de $m$ et démontrer que $z$ et $m$ sont congrus modulo 12.
- Retrouver alors la date de l'anniversaire d'un spectateur ayant obtenu le nombre $474$ en appliquant le programme de calcul (A).
Partie B
Lors d'une autre représentation, le magicien décide de changer son programme de calcul. Pour un spectateur dont le numéro du jour de naissance est $j$ et le numéro du mois de naissance est $m$, le magicien demande de calculer le nombre $z$ défini par $z = 12j + 31m$. Dans les questions suivantes, on étudie différentes méthodes permettant de retrouver la date d'anniversaire du spectateur.
- Première méthode : On considère l'algorithme suivant : $$\begin{array}{|l l|}\hline \text{Variables :}&j \text{ et } m \text{ sont des entiers naturels}\\ \text{Traitement :}& \text{ Pour } m \text{ allant de 1 à 12 faire :}\\ & \begin{array}{|l} \text{ Pour } j \text{ allant de 1 à 31 faire :}\\ \begin{array}{|l} z \text{ prend la valeur } 12j + 31m\\ \text{Afficher } z\\ \end{array}\\ \text{Fin Pour }\\ \end{array}\\ &\text{ Fin Pour }\\ \hline \end{array}$$ Modifier cet algorithme afin qu'il affiche toutes les valeurs de $j$ et de $m$ telles que $12j + 31m = 503$.
- Deuxième méthode :
- Démontrer que $7m$ et $z$ ont le même reste dans la division euclidienne par 12.
- Pour $m$ variant de 1 à 12, donner le reste de la division euclidienne de $7m$ par 12.
- En déduire la date de l'anniversaire d'un spectateur ayant obtenu le nombre $503$ avec le programme de calcul (B).
- Troisième méthode :
- Démontrer que le couple $(-2~;~17)$ est solution de l'équation $12x + 31y = 503$.
- En déduire que si un couple d'entiers relatifs $(x~;~y)$ est solution de l'équation $12x + 31y = 503$, alors $12(x + 2) = 31 (17 - y)$.
- Déterminer l'ensemble de tous les couples d'entiers relatifs $(x ; y)$, solutions de l'équation $12x + 31y = 503$.
- Démontrer qu'il existe un unique couple d'entiers relatifs $(x~;~y)$ tel que $1 \leqslant y \leqslant 12$. En déduire la date d'anniversaire d'un spectateur ayant obtenu le nombre $503$ avec le programme de calcul (B).
Correction de l'exercice de spécialité (5 points)
Par exemple, pour une personne née le 14 mai, le numéro du jour de naissance est 14 et le numéro du mois de naissance est 5.
Partie A
Lors d'une représentation, un magicien demande aux spectateurs d'effectuer le programme de calcul (A) suivant : « Prenez le numéro de votre jour de naissance et multipliez-le par 12. Prenez le numéro de votre mois de naissance et multipliez-le par 37. Ajoutez les deux nombres obtenus. Je pourrai alors vous donner la date de votre anniversaire » . Un spectateur annonce $308$ et en quelques secondes, le magicien déclare : « Votre anniversaire tombe le 1er août ! » .
- Vérifier que pour une personne née le 1er août, le programme de calcul (A) donne effectivement le nombre $308$.
- Numéro du jour de naissance multiplié par 12: $j=1\times 12=12$;
- Numéro du mois de naissance multiplié par 37: $m=8\times 37=296$;
- $m+j=308$.
-
- Pour un spectateur donné, on note $j$ le numéro de son jour de naissance, $m$ celui de son mois de naissance et $z$ le résultat obtenu en appliquant le programme de calcul (A). Exprimer $z$ en fonction de $j$ et de $m$ et démontrer que $z$ et $m$ sont congrus modulo 12.
- Retrouver alors la date de l'anniversaire d'un spectateur ayant obtenu le nombre $474$ en appliquant le programme de calcul (A). $$ z=474=12j+37\times 6\Longrightarrow 12j=474-37\times 6=252=21\times 12\Longrightarrow j=21 $$ Le spectateur est donc né un 21 juin.
Date de l'anniversaire d'un spectateur ayant obtenu le nombre $474$ en appliquant le programme de calcul (A): $$ \left\lbrace\begin{array}{l} z=474=39\times 12+6\\ z\equiv 37m\ [12] \end{array}\right.\Longrightarrow z=(3\times 12+1)m\equiv 6\ [12]\Longrightarrow m\equiv 6\ [12], \text{le mois est donc juin} $$
Partie B
Lors d'une autre représentation, le magicien décide de changer son programme de calcul. Pour un spectateur dont le numéro du jour de naissance est $j$ et le numéro du mois de naissance est $m$, le magicien demande de calculer le nombre $z$ défini par $z = 12j + 31m$. Dans les questions suivantes, on étudie différentes méthodes permettant de retrouver la date d'anniversaire du spectateur.
- Première méthode : On considère l'algorithme suivant : $$\begin{array}{|l l|}\hline \text{Variables :}&j \text{ et } m \text{ sont des entiers naturels}\\ \text{Traitement :}& \text{ Pour } m \text{ allant de 1 à 12 faire :}\\ & \begin{array}{|l} \text{ Pour } j \text{ allant de 1 à 31 faire :}\\ \begin{array}{|l} z \text{ prend la valeur } 12j + 31m\\ \text{Afficher } z\\ \end{array}\\ \text{Fin Pour }\\ \end{array}\\ &\text{ Fin Pour }\\ \hline \end{array}$$ Modifier cet algorithme afin qu'il affiche toutes les valeurs de $j$ et de $m$ telles que $12j + 31m = 503$.
- Deuxième méthode :
- Démontrer que $7m$ et $z$ ont le même reste dans la division euclidienne par 12.
- Pour $m$ variant de 1 à 12, donner le reste de la division euclidienne de $7m$ par 12. $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline m & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12\\ \hline\text{ reste }& 7 & 2 & 9 & 4 & 11 & 6 & 1 & 8 & 3 & 10 & 5 & 0\\ \hline \end{array}$$ On remarque qu'à chacun des 12 restes possibles correspond un seul mois.
- En déduire la date de l'anniversaire d'un spectateur ayant obtenu le nombre $503$ avec le programme de calcul (B).
$12a\equiv 0\ [12]$ pour tout $a$ entier, donc $$ z=12j+31m\equiv 31m=(2\times 12+7)m=12\times 2m+7m\equiv 7m\ [12] $$ $7m$ et $z$ ont donc le même reste dans la division euclidienne par 12.
Date de l'anniversaire d'un spectateur ayant obtenu le nombre $503$ avec le programme de calcul (B): $$ \left\lbrace\begin{array}{l} z=503=41\times 12+11\\ z\equiv 7m\ [12] \end{array}\right.\Longrightarrow 7m\equiv 11\ [12]\Longrightarrow m=5,\ \text{le mois est donc mai} $$ $$ z=503=12j+31\times 5\Longrightarrow 12j=503-31\times 5=29\times 12\Longrightarrow j=29 $$ Le spectateur est donc né un 29 mai. - Troisième méthode :
- Démontrer que le couple $(-2~;~17)$ est solution de l'équation $12x + 31y = 503$.
- En déduire que si un couple d'entiers relatifs $(x~;~y)$ est solution de l'équation $12x + 31y = 503$, alors $12(x + 2) = 31 (17 - y)$.
- Déterminer l'ensemble de tous les couples d'entiers relatifs $(x ; y)$, solutions de l'équation $12x + 31y = 503$.
- Partie directe: $$ 12x + 31y = 503\Longrightarrow \left\lbrace\begin{array}{l} 12(x + 2) = 31 (17 - y)\\ \text{pgcd}(12;31)=1 \end{array}\right.\stackrel{\text{\text{Gauss}}}{\Longrightarrow} 31\ \text{divise}\ x+2 $$ Ainsi, il existe un entier relatif $k$ vérifiant $x+2=31k\Longleftrightarrow \boxed{x=-2+31k}$. En remplaçant dans $(E)$, on obtient: $$ \left\lbrace\begin{array}{l} 12(x + 2) = 31 (17 - y)\\ x+2=31k \end{array}\right.\Longrightarrow 12\times {31}k={31}(17-y)\Longleftrightarrow 12k=17-y\Longleftrightarrow \boxed{y=17-12k} $$
- Réciproque: pour tout $k$ de $\mathbb{Z}$, on a: $$ 12(-2+31k)+31(17-12k)=\underbrace{12\times(-2) + 31\times(17)}_{503}+{12\times 31k}-{12\times 31k}=503 $$
- Pour tout $k$ de $\mathbb{Z}$, le couple $(x;y)=(-2+31k;17-12k)$ est solution de $12x + 31y = 503$.
- Démontrer qu'il existe un unique couple d'entiers relatifs $(x~;~y)$ tel que $1 \leqslant y \leqslant 12$. En déduire la date d'anniversaire d'un spectateur ayant obtenu le nombre $503$ avec le programme de calcul (B).
Le couple $(-2~;~17)$ est solution de l'équation $12x + 31y = 503$: $$ 12\times(-2) + 31\times(17) = 503 $$
Un couple d'entiers relatifs $(x~;~y)$ est solution de l'équation $12x + 31y = 503$: $$ \left\lbrace\begin{array}{lr} 12x + 31y = 503& L_1\\ 12\times(-2) + 31\times(17) = 503& L_2 \end{array}\right.\Longrightarrow 12(x+2)+31(y-17)=0\ (L_1-L_2)\Longleftrightarrow 12(x + 2) = 31 (17 - y)\ (E) $$
Résolution de l'équation $12x + 31y = 503$:
Il existe un unique couple d'entiers relatifs $(x~;~y)$ tel que $1 \leqslant y \leqslant 12$: $$ 1 \leqslant y \leqslant 12 \Longleftrightarrow 1 \leqslant 17-12k \leqslant 12 \Longleftrightarrow -16 \leqslant -12k \leqslant -5 \Longleftrightarrow 5 \leqslant 12k \leqslant 16 \Longleftrightarrow \frac{5}{12} \leqslant k \leqslant \frac{16}{12} $$ Ainsi $k=1$ est l'unique entier compris entre $\dfrac{5}{12}\simeq 0,4166$ et $\dfrac{16}{12}\simeq 1,3333$ . L'unique couple recherché est donc: $(-2+31\times 1;17-12\times 1)=(29;5)$
Le spectateur est donc né un 29 mai.
Première méthode : Algorithme modifié ($\texttt{AlgoBox}$) pour qu'il affiche toutes les valeurs de $j$ et de $m$ telles que $12j + 31m = 503$.

Le spectateur est donc né un 29 mai.
- Vues: 35680
