Baccalauréat S Nouvelle-Calédonie 14 novembre 2013
Exercice 1 5 points
Soit $f$ la fonction dérivable, définie sur l'intervalle $]0 ; +\infty[$ par
\[f(x) = \text{e}^x + \dfrac{1}{x}.\]
- Étude d'une fonction auxiliaire
- Soit la fonction $g$ dérivable, définie sur $[0 ; +\infty[$ par \[g(x) = x^2\text{e}^x - 1.\] Étudier le sens de variation de la fonction $g$.
- Démontrer qu'il existe un unique réel $a$ appartenant à $[0 ; +\infty[$ tel que $g(a) = 0$. Démontrer que $a$ appartient à l'intervalle [0,703 ; 0,704[.
- Déterminer le signe de $g(x)$ sur $[0 ; +\infty[$.
- Étude de la fonction h $f$
- Déterminer les limites de la fonction $f$ en $0$ et en $+ \infty$.
- On note $f'$ la fonction dérivée de $f$ sur l'intervalle $]0 ; +\infty[$. Démontrer que pour tout réel strictement positif $x,\: f'(x) = \dfrac{g(x)}{x^2}$.
- En déduire le sens de variation de la fonction $f$ et dresser son tableau de variation sur l'intervalle $]0 ; +\infty[$.
- Démontrer que la fonction $f$ admet pour minimum le nombre réel $m = \dfrac{1}{a^2} + \dfrac{1}{a}$.
- Justifier que $3,43 < m < 3,45$.
Exercice 1 5 points
Soit $f$ la fonction dérivable, définie sur l'intervalle $]0 ; +\infty[$ par
\[f(x) = \text{e}^x + \dfrac{1}{x}.\]
- Étude d'une fonction auxiliaire
- Soit la fonction $g$ dérivable, définie sur $[0 ; +\infty[$ par \[g(x) = x^2\text{e}^x - 1.\] Étudier le sens de variation de la fonction $g$. $g'(x) = 2x\text{e}^x + x^2\text{e}^x = x\text{e}^x(2+x)$.
- Démontrer qu'il existe un unique réel $a$ appartenant à $[0 ; +\infty[$ tel que $g(a) = 0$. Démontrer que $a$ appartient à l'intervalle [0,703 ; 0,704[. $g$ est continue et strictement croissante sur $[0;+\infty[$.
- $\1 $ est une fonction dérivable donc continue sur l' intervalle $I = \left[\2 ; \3\right[$.
- $\1$ est strictement croissante sur l' intervalle $I = \left[\2 ; \3\right[$.
- $\1 \left(\2\right)=\4$ et $\lim\limits_{x \to \3}~\1(x)=\5$
- Déterminer le signe de $g(x)$ sur $[0 ; +\infty[$. Par conséquent, en utilisant le fait que $g$ est strictement croissante sur $[0;+\infty[$
Par conséquent sur $[0;+\infty[$, $g'(x) \ge 0$ (et ne s’annule qu’en $0$) et $g$ est strictement croissante sur $[0;+\infty[$.
$g(0) = -1$
$\lim\limits_{x \rightarrow +\infty} x^2 = +\infty$ , $\lim\limits_{x \rightarrow +\infty} \text{e}^x = +\infty$ donc $\lim\limits_{x \rightarrow +\infty}g(x) = +\infty$.
D'après le théorème de la bijection :
$\6\in \left[\4;\5\right[$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left[\2 ; \3\right[$ .Encadrement de $\alpha$ à $10^{-\2}$ pès :
Avec une calculatrice on obtient :
$\3\left(\4\right)\approx \5$ et $\3\left(\6\right)\approx \7$
On a donc $\3\left(\4\right)<\8<\3\left(\6\right)$, soit $\3\left(\4\right)<\3\left(\1\right)<\3\left(\6\right)$
comme $\3$ est strictement croissante sur $\left[\9;\10\right]$; on déduit $\4<\1< \6$$$\4<\1< \6$$
$g(x) < 0$ sur $[0;a[$, $g(a) = 0$ et $g(x) > 0$ sur $]a;+\infty[$.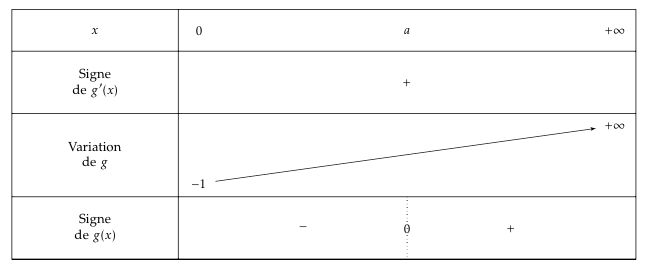
- Étude de la fonction h $f$
- Déterminer les limites de la fonction $f$ en $0$ et en $+ \infty$. $\lim\limits_{x \rightarrow 0^{+}} \text{e}^x = 1$ et $\lim\limits_{x \rightarrow 0^+} \dfrac{1}{x} = +\infty$ donc $\lim\limits_{x \rightarrow 0^+} f(x) = +\infty$.
- On note $f'$ la fonction dérivée de $f$ sur l'intervalle $]0 ; +\infty[$. Démontrer que pour tout réel strictement positif $x,\: f'(x) = \dfrac{g(x)}{x^2}$. $f$ est une somme de fonctions dérivables sur $]0;+\infty[$; elle est donc également dérivable sur cet intervalle.
- En déduire le sens de variation de la fonction $f$ et dresser son tableau de variation sur l'intervalle $]0 ; +\infty[$. Le signe de $f'(x)$ ne dépend donc que de celui de $g(x)$
- Démontrer que la fonction $f$ admet pour minimum le nombre réel $m = \dfrac{1}{a^2} + \dfrac{1}{a}$. $f$ admet donc un minimum en $a$. Or $g(a) = a^2\text{e}^a-1 = 0$.
- Justifier que $3,43 < m < 3,45$. $0,703 < a < 0,704$ donc $\dfrac{1}{0,704} < \dfrac{1}{a} < \dfrac{1}{0,703}$
$\lim\limits_{x \rightarrow +\infty} \text{e}^x = +\infty$ et $\lim\limits_{x \rightarrow +\infty} \dfrac{1}{x} = 0$ donc $\lim\limits_{x \rightarrow +\infty} f(x) = +\infty$.
Et $f'(x) = \text{e}^x – \dfrac{1}{x^2} = \dfrac{x^2 \text{e}^x-1}{x^2} = \dfrac{g(x)}{x^2}$.
d’où $\text{e}^a = \dfrac{1}{a^2}$.
$m= f(a) = \text{e}^a + \dfrac{1}{a} = \dfrac{1}{a^2}+\dfrac{1}{a}$.
On a donc également $\dfrac{1}{0,704^2} < \dfrac{1}{a^2} < \dfrac{1}{0,703^2}$ Soit $\dfrac{1}{0,704} + \dfrac{1}{0,704^2} < m < \dfrac{1}{0,703} + \dfrac{1}{0,703^2}$
D’où $3,43 < m < 3,45$.
Exercice 2 5 points
Soient deux suites $\left(u_{n}\right)$ et $\left(v_{n}\right)$ définies par $u_{0} = 2$ et $v_{0} = 10$ et pour tout entier naturel $n$, \[u_{n+1} = \dfrac{2u_{n} + v_{n}}{3} \quad \text{et}\quad v_{n+1} = \dfrac{u_{n} + 3v_{n}}{4}.\]
PARTIE A
On considère l'algorithme suivant :
$$\begin{array}{ |c|c|}\hline \text{Variables :}& N \text{ est un entier }\\ &U, V, W \text{ sont des réels}\\ &K \text{est un entier } \\ \text{Début :}& \text{ Affecter 0 à } K\\ & \text{ Affecter 2 à } U \\ &\text{ Affecter 10 à } V\\ &\text{ Saisir } N\\ &\text{ Tant que } K < N\\ & \text{ Affecter } K + 1 \text{ à } K\\ & \text{ Affecter } U \text{ à } W\\ & \text{ Affecter } \dfrac{2U+V}{3} \text{ à } U\\ & \text{ Affecter } \dfrac{W+3V}{4} \text{ à } V\\ &\text{ Fin tant que }\\ &\text{Afficher } U \\ &\text{ Afficher } V\\ \text{Fin}&\\ \hline \end{array}$$
PARTIE B
-
- Montrer que pour tout entier naturel $n,\: v_{n+1} - u_{n+1} = \dfrac{5}{12} \left(v_{n} - u_{n}\right)$.
- Pour tout entier naturel $n$ on pose $w_{n} = v_{n} - u_{n}$. Montrer que pour tout entier naturel $n,\: w_{n} = 8 \left(\dfrac{5}{12} \right)^n$.
-
- Démontrer que la suite $\left(u_{n}\right)$ est croissante et que la suite $\left(v_{n}\right)$ est décroissante.
- Déduire des résultats des questions 1. b. et 2. a. que pour tout entier naturel $n$ on a $u_{n} \leqslant 10$ et $v_{n} \geqslant 2$.
- En déduire que tes suites $\left(u_{n}\right)$ et $\left(v_{n}\right)$ sont convergentes.
- Montrer que les suites $\left(u_{n}\right)$ et $\left(v_{n}\right)$ ont la même limite.
- Montrer que la suite $\left(t_{n}\right)$ définie par $t_{n} = 3u_{n} + 4v_{n}$ est constante. En déduire que la limite commune des suites $\left(u_{n}\right)$ et $\left(v_{n}\right)$ est $\dfrac{46}{7}$.
Exercice 2 5 points
Soient deux suites $\left(u_{n}\right)$ et $\left(v_{n}\right)$ définies par $u_{0} = 2$ et $v_{0} = 10$ et pour tout entier naturel $n$, \[u_{n+1} = \dfrac{2u_{n} + v_{n}}{3} \quad \text{et}\quad v_{n+1} = \dfrac{u_{n} + 3v_{n}}{4}.\]
PARTIE A
On considère l'algorithme suivant :
$$\begin{array}{ |c|c|}\hline \text{Variables :}& N \text{ est un entier }\\ &U, V, W \text{ sont des réels}\\ &K \text{est un entier } \\ \text{Début :}& \text{ Affecter 0 à } K\\ & \text{ Affecter 2 à } U \\ &\text{ Affecter 10 à } V\\ &\text{ Saisir } N\\ &\text{ Tant que } K < N\\ & \text{ Affecter } K + 1 \text{ à } K\\ & \text{ Affecter } U \text{ à } W\\ & \text{ Affecter } \dfrac{2U+V}{3} \text{ à } U\\ & \text{ Affecter } \dfrac{W+3V}{4} \text{ à } V\\ &\text{ Fin tant que }\\ &\text{Afficher } U \\ &\text{ Afficher } V\\ \text{Fin}&\\ \hline \end{array}$$
| K | W | U | V |
| $0$ | $2$ | $10$ | |
| $1$ | $2$ | $\frac{14}{3}$ | $8$ |
| $2$ | $\frac{14}{3}$ | $\frac{52}{9}$ | $\frac{43}{6}$ |
PARTIE B
-
- Montrer que pour tout entier naturel $n,\: v_{n+1} - u_{n+1} = \dfrac{5}{12} \left(v_{n} - u_{n}\right)$. $v_{n+1} – u_{n+1} = \dfrac{u_n+3v_n}{4}-\dfrac{2u_n+v_n}{3} = \dfrac{3u_n+9v_n-8u_n-4v_n}{12}$
- Pour tout entier naturel $n$ on pose $w_{n} = v_{n} - u_{n}$. Montrer que pour tout entier naturel $n,\: w_{n} = 8 \left(\dfrac{5}{12} \right)^n$. On a donc $w_{n+1} = \dfrac{5}{12}w_n$ et $w_0 = 10 – 2 = 8$.
$v_{n+1} – u_{n+1} = \dfrac{-5u_n+5v_n}{12} = \dfrac{5}{12}(v_n-u_n)$
$(w_n)$ est donc une suite géoémtrique de raison $\dfrac{5}{12}$ et de premier terme $8$.
D’où $w_n = 8 \times \left(\dfrac{5}{12} \right)^n$. -
- Démontrer que la suite $\left(u_{n}\right)$ est croissante et que la suite $\left(v_{n}\right)$ est décroissante. $u_{n+1} – u_n = \dfrac{2u_n+v_n}{3} – u_n = \dfrac{v_n-u_n}{3} = \dfrac{w_n}{3} > 0$.
- Déduire des résultats des questions 1. b. et 2. a. que pour tout entier naturel $n$ on a $u_{n} \leqslant 10$ et $v_{n} \geqslant 2$. On a donc $u_0 <u_1< … < u_n < … <v_n < … < v_1 < v_0$.
- En déduire que tes suites $\left(u_{n}\right)$ et $\left(v_{n}\right)$ sont convergentes. La suite $(u_n)$ est croissante et majorée; elle converge donc.
La suite $(u_n)$ est donc croissante.
$v_{n+1} – v_n = \dfrac{u_n+3v_n}{4} – v_n = \dfrac{u_n-v_n}{4} = \dfrac{-w_n}{4} < 0$.
La suite $(v_n)$ est donc décroissante.
On ne peut pas trouver $2$ indices $n$ et $m$ tels que $u_n > v_m$.
En effet, si $n < m$ alors $u_m > u_n > v_m$ ce qui est impossible car $v_n – u_n > 0$ pour tout $n$.
Si $n > m$ alors $u_n > v_m > v_n$ ce qui est encore impossible.
Donc, pour tout $n$, on a $b_n \ge u_0 = 2$ et $u_n \le v_0 = 10$.
Remarque : les suites $(u_n)$ et $(v_n)$ sont dites adjacentes
De même, la suite $(v_n)$ est décroissante et minorée. Elle converge aussi. - Montrer que les suites $\left(u_{n}\right)$ et $\left(v_{n}\right)$ ont la même limite. On appelle $U$ et $V$ les limites des suites $(u_n)$ et $(v_n)$.
- Montrer que la suite $\left(t_{n}\right)$ définie par $t_{n} = 3u_{n} + 4v_{n}$ est constante. En déduire que la limite commune des suites $\left(u_{n}\right)$ et $\left(v_{n}\right)$ est $\dfrac{46}{7}$. $t_{n+1} = 3u_{n+1} + 4v_{n+1} = 2u_n+v_n+u_n+3v_n = 3u_n+4v_n = t_n$.
On a donc $U = \dfrac{2U+V}{3}$ et $V = \dfrac{U+3V}{4}$.
D’où $3U=2U+V \Leftrightarrow U = V$.
Les $2$ suites ont donc bien la même limite $U$.
La suite $(t_n)$ est donc constante et, pour tout $n$, on a donc $t_n = t_0 = 3u_0+4v_0=46$.
En passant à la limite on obtient alors $46 = 3U + 4U$ soit $U = \dfrac{46}{7}$.
Exercice 3 5 points
Tous les résultats numériques devront être donnés sous forme décimale et arrondis au dix-millième.
Une usine fabrique des billes sphériques dont le diamètre est exprimé en millimètres. Une bille est dite hors norme lorsque son diamètre est inférieur à 9 mm ou supérieur à 11 mm.
Partie A
- On appelle $X$ la variable aléatoire qui à chaque bille choisie au hasard dans la production associe son diamètre exprimé en mm. On admet que la variable aléatoire $X$ suit la loi normale d'espérance $10$ et d'écart-type $0,4$.
Montrer qu'une valeur approchée à 0,0001 près de la probabilité qu'une bille soit hors norme est 0,0124 . On pourra utiliser la table de valeurs donnée en annexe. - On met en place un contrôle de production tel que 98 % des billes hors norme sont écartés et 99 % des billes correctes sont conservées. On choisit une bille au hasard dans la production. On note $N$ l'évènement : «la bille choisie est aux normes », $A$ l'évènement : «la bille choisie est acceptée à l'issue du contrôle ».
- Construire un arbre pondéré qui réunit les données de l'énoncé.
- Calculer la probabilité de l'évènement $A$.
- Quelle est la probabilité pour qu'une bille acceptée soit hors norme ?
Partie B
Ce contrôle de production se révélant trop coûteux pour l'entreprise, il est abandonné : dorénavant, toutes les billes produites sont donc conservées, et elles sont conditionnées par sacs de 100 billes. On considère que la probabilité qu'une bille soit hors norme est de \np{0,0124}. On admettra que prendre au hasard un sac de $100$ billes revient à effectuer un tirage avec remise de $100$ billes dans l'ensemble des billes fabriquées. On appelle $Y$ la variable aléatoire qui à tout sac de $100$ billes associe le nombre de billes hors norme de ce sac.
- Quelle est la loi suivie par la variable aléatoire $Y$ ?
- Quels sont l'espérance et l'écart-type de la variable aléatoire $Y$ ?
- Quelle est la probabilité pour qu'un sac de $100$ billes contienne exactement deux billes hors norme ?
- Quelle est la probabilité pour qu'un sac de $100$ billes contienne au plus une bille hors norme ?
Exercice 3 5 points
Tous les résultats numériques devront être donnés sous forme décimale et arrondis au dix-millième.
Une usine fabrique des billes sphériques dont le diamètre est exprimé en millimètres. Une bille est dite hors norme lorsque son diamètre est inférieur à 9 mm ou supérieur à 11 mm.
Partie A
- On appelle $X$ la variable aléatoire qui à chaque bille choisie au hasard dans la production associe son diamètre exprimé en mm. On admet que la variable aléatoire $X$ suit la loi normale d'espérance $10$ et d'écart-type $0,4$.
Montrer qu'une valeur approchée à 0,0001 près de la probabilité qu'une bille soit hors norme est 0,0124 . On pourra utiliser la table de valeurs donnée en annexe.- Avec la table :
On cherche donc :
$P\left( (X <9) \cup (X > 11) \right) = P(X < 9) + P(X > 11)$ car les événements sont disjoints.
$P\left( (X <9) \cup (X > 11) \right) = 0,00620967 + 1 – P(X < 11) = 0,00620967 + 1 – 0,99379034 = 0,01241933$
$P\left( (X <9) \cup (X > 11) \right) = 0,01241933 \approx 0,0124$.
Remarque : attention à ne pas confondre les numéros des lignes de calcul avec la valeur de $d$ dans l’annexe ! - Avec la calculatrice :
2ND DISTR 2NORMALFRép( -10^(99) , \1,$\2$,$\3$)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(-10^{99},\1,\2,\3) \approx \4$$
$$P( \5 \leq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$
$$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$Ainsi $P\left( (X <9) \cup (X > 11) \right) =2\times 0,00620967 = 0,01241933$.
- Avec la table :
- On met en place un contrôle de production tel que 98 % des billes hors norme sont écartés et 99 % des billes correctes sont conservées. On choisit une bille au hasard dans la production. On note $N$ l'évènement : «la bille choisie est aux normes », $A$ l'évènement : «la bille choisie est acceptée à l'issue du contrôle ».
- Construire un arbre pondéré qui réunit les données de l'énoncé.
- Calculer la probabilité de l'évènement $A$. $p(A) = p(A \cap N) + p(A \cap \bar{N})$ (d’après la formule des probabilités totales).
- Quelle est la probabilité pour qu'une bille acceptée soit hors norme ? On cherche $p_A(\bar{N}) = \dfrac{p(A \cap \bar{N})}{p(A} = \dfrac{0,0124 \times 0,02}{0,9780} \approx 3 \times 10^{-4}$.
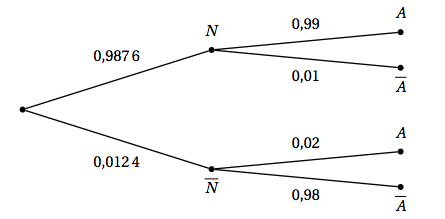
$p(A) = 0,9876 \times 0,99 + 0,0124 \times 0,02 = 0,9780$.
Partie B
Ce contrôle de production se révélant trop coûteux pour l'entreprise, il est abandonné : dorénavant, toutes les billes produites sont donc conservées, et elles sont conditionnées par sacs de 100 billes. On considère que la probabilité qu'une bille soit hors norme est de 0,0124 . On admettra que prendre au hasard un sac de $100$ billes revient à effectuer un tirage avec remise de $100$ billes dans l'ensemble des billes fabriquées. On appelle $Y$ la variable aléatoire qui à tout sac de $100$ billes associe le nombre de billes hors norme de ce sac.
- Quelle est la loi suivie par la variable aléatoire $Y$ ?
- « \3 » considéré comme succès, de probabilité $p=\4$
- « \5 » considéré comme échec, de probabilité $q=1-p=\6$
- Quels sont l'espérance et l'écart-type de la variable aléatoire $Y$ ? $E(Y) = np = 1,24$ et $\sigma(Y) = \sqrt{np(1-p)} \approx 1,1066$.
- Quelle est la probabilité pour qu'un sac de $100$ billes contienne exactement deux billes hors norme ?
- Quelle est la probabilité pour qu'un sac de $100$ billes contienne au plus une bille hors norme ? $P(Y \le 1) = P(Y=0) + P(Y=1) $
On répète $\1$ fois, de façon indépendante, l’expérience «\2 » qui comporte 2 issues :
Nous sommes donc en présence d’un schéma de Bernoulli et la variable aléatoire $\7$ prenant pour valeurs le nombre de succès obtenus suit la loi binomiale de paramètres $\1$ et $\4$ notée $\mathscr{B}(\1;\4)$ .
Pour tout entier $k$ où $0\leq k\leq \1$, on a $$P(\7=k)=\binom{\1}{k}\times \left(\4\right)^k\times\left( \6\right)^{\1-k}$$
2ND DISTR 0binomFdP( \1 , \2,\3)EXE
Avec une calculatrice de type TI $binomFdP(\1,\2,\3) \approx \4$
$P(Y \le 1) = (1-0,0124)^100 + \binom{100}{1}\times 0,0124 \times (1-0,0124)^{99} \approx 0,6477$
ou de façon plus directe:
2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$
Exercice 4 5 points
Le plan est rapporté à un repère orthonormal direct $\left(\text{O},\vec{u},\vec{v}\right)$.
On note $\mathbb{C}$ l'ensemble des nombres complexes.
Pour chacune des propositions suivantes, dire si elle est vraie ou fausse en justifiant la réponse.
- Proposition : Pour tout entier naturel $n :\: (1 + \text{i})^{4n} = (- 4)^n$.
- Soit (E) l'équation $(z - 4)\left(z^2 - 4z + 8\right) = 0$ où $z$ désigne un nombre complexe.
Proposition : Les points dont les affixes sont les solutions, dans $\mathbb{C}$, de (E) sont les sommets d'un triangle d'aire 8. - Proposition : Pour tout nombre réel $\alpha,\: 1 + \text{e}^{2i\alpha} = 2\text{e}^{\text{i}\alpha} \cos(\alpha)$.
- Soit A le point d'affixe $z_{\text{A}} = \dfrac{1}{2}(1 + \text{i})$ et $M_{n}$ le point d'affixe $\left(z_{\text{A}}\right)^n$ où $n$ désigne un entier naturel supérieur ou égal à $2$.
Proposition : si $n - 1$ est divisible par 4, alors les points O, A et $M_{n}$ sont alignés. - Soit j le nombre complexe de module 1 et d'argument $\dfrac{2\pi}{3}$.
Proposition : $1 + \text{j} + \text{j}^2 = 0$.
Exercice 4 5 points
Le plan est rapporté à un repère orthonormal direct $\left(\text{O},\vec{u},\vec{v}\right)$.
On note $\mathbb{C}$ l'ensemble des nombres complexes.
Pour chacune des propositions suivantes, dire si elle est vraie ou fausse en justifiant la réponse.
- Proposition : Pour tout entier naturel $n :\: (1 + \text{i})^{4n} = (- 4)^n$. Affirmation vraie
- Soit (E) l'équation $(z - 4)\left(z^2 - 4z + 8\right) = 0$ où $z$ désigne un nombre complexe.
Proposition : Les points dont les affixes sont les solutions, dans $\mathbb{C}$, de (E) sont les sommets d'un triangle d'aire 8. Affirmation fausse - Proposition : Pour tout nombre réel $\alpha,\: 1 + \text{e}^{2i\alpha} = 2\text{e}^{\text{i}\alpha} \cos(\alpha)$. Affirmation vraie
- Soit A le point d'affixe $z_{\text{A}} = \dfrac{1}{2}(1 + \text{i})$ et $M_{n}$ le point d'affixe $\left(z_{\text{A}}\right)^n$ où $n$ désigne un entier naturel supérieur ou égal à $2$.
Proposition : si $n - 1$ est divisible par 4, alors les points O, A et $M_{n}$ sont alignés. Affirmation vraie - Soit j le nombre complexe de module 1 et d'argument $\dfrac{2\pi}{3}$.
Proposition : $1 + \text{j} + \text{j}^2 = 0$. Affirmation vraie
>$(1+\text{i})^{4n} = \left((1+\text{i})^4 \right)^n = \left( \left(\sqrt{2}\text{e}^{\text{i}\pi /4}\right)^4 \right)^n = (4\text{e}^{\text{i}\pi})^n = (-4)^n$
Cherchons les solutions de $z^2-4z+8 = 0$.
$\Delta = (-4)^2-4\times 8 = -16 < 0$.
Cette équation possède donc $2$ solutions complexes :
$\dfrac{4-4\text{i}}{2} = 2 – 2\text{i}$ et $2 + 2\text{i}$.
Les solutions de (E) sont donc les nombres $4$, $2 – 2\text{i}$ et $2 + 2\text{i}$.
On appelle $A$, $B$ et $C$ les points dont ces nombres sont les affixes.
$B$ et $C$ sont symétriques par rapport à l’axe des abscisses et $A$ est sur c et axe.
Par conséquent $ABC$ est isocèle en $A$.
Le milieu de $[BC]$ a pour affixe $2$ et $BC = |z_C – z_B| = |4\text{i}| = 4$.
L’aire du triangle $ABC$ est donc $\dfrac{4\times(4-2)}{2} = 4$.
$1 + \text{e}^{2\text{i}\alpha} = 1 + \cos(2\alpha) + \text{i} \sin(2\alpha) = 1 + 3\cos^2(\alpha) – 1 + 2\text{i}\sin(\alpha)\cos(\alpha)$
$1 + \text{e}^{2\text{i}\alpha} =2\cos^2(\alpha)+2\text{i}\sin(\alpha)\cos(\alpha) = 2\cos(\alpha)\left( \cos(\alpha) + \text{i}\sin(\alpha) \right) = 2\text{e}^{\text{i}\alpha}\cos(\alpha)$.
affixe de $\vec{OA} : a = \dfrac{1}{2}(1+i)$
affixe de $\vec{OM_n} : m_n = \left(\dfrac{1}{2}(1+i) \right)^n$.
$O$, $A$ et $M_n$ sont alignés $\Leftrightarrow \dfrac{m_n}{a}\in \mathbb R$.
Or $\dfrac{m_n}{a} = \left( \dfrac{1}{2}(1+i)\right) ^{n-1} = \left( \dfrac{1}{2}\left(\sqrt{2}\text{e}^{\text{i}\pi/4} \right) \right)^{n-1} = \dfrac{\sqrt{2}^{n-1}}{2^{n-1}}\text{e}^{(n-1)\text{i}\pi/4}$
$\dfrac{m_n}{a}\in \mathbb R \Leftrightarrow \dfrac{n-1}{4}\in \mathbb N \Leftrightarrow n-1$ divisible par $4$.
$j=\text{e}^{2\text{i}\pi/3} = \cos \dfrac{2\pi}{3} + \text{i} \sin \dfrac{2\pi}{3} = -0,5 + \dfrac{\sqrt{3}}{2}\text{i}$.
Donc $j^2 = \text{e}^{4\text{i}\pi/3} = \cos \dfrac{4\pi}{3} + \text{i}\sin \dfrac{4\pi}{3} = -0,5 – \dfrac{\sqrt{3}}{2}\text{i}$
Finalement $1+j+j^2 = 1 – 0,5 + \dfrac{\sqrt{3}}{2}\text{i} – 0,5 – \dfrac{\sqrt{3}}{2}\text{i} = 0$
remarque : on pouvait également dire que $1+j+j^2 = \dfrac{1-j^3}{1-j}$.
Et $1-j^3 = 1 – \text{e}^{2\text{i}\pi}=0$.
Spécialité 5 points
On note $E$ l'ensemble des vingt-sept nombres entiers compris entre $0$ et $26$.
On note $A$ l'ensemble dont les éléments sont les vingt-six lettres de l'alphabet et un séparateur entre deux mots, noté «$\star$ » considéré comme un caractère.
Pour coder les éléments de $A$, on procède de la façon suivante :
Premièrement : On associe à chacune des lettres de l'alphabet, rangées par ordre alphabétique, un nombre entier naturel compris entre 0 et 25, rangés par ordre croissant. On a donc $a \to 0,\: b \to 1, \ldots z \to 25$.
On associe au séparateur «$\star$ » le nombre 26.
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline a&b&c&d&e&f&g&h&i&j&k&l&m&n\\ \hline 0&1&2&3&4&5&6&7&8&9&10&11&12&13\\ \hline \end{array}$$
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline o&p&q&r&s&t&u&v&w&x&y&z&\star \\ \hline 14&15&13&17&18&19&20&21&22&23&24&25&26 \\ \hline \end{array}$$
On dit que $a$ a pour rang $0, b$ a pour rang 1, ... , $z$ a pour rang $25$ et le séparateur «$\star$ » a pour rang $26$.
Deuxièmement : à chaque élément $x$ de $E$, l'application $g$ associe le reste de la division euclidienne de $4x + 3$ par $27$.
On remarquera que pour tout $x$ de $E,\: g(x)$ appartient à $E$.
Troisièmement : Le caractère initial est alors remplacé par le caractère de rang $g(x)$. Exemple : $s \to 18, \quad g(18) = 21$ et $21 \to v$. Donc la lettre $s$ est remplacée lors du codage par la lettre $v$.
- Trouver tous les entiers $x$ de $E$ tels que $g(x) = x$ c'est-à-dire invariants par $g$.
En déduire les caractères invariants dans ce codage. - Démontrer que, pour tout entier naturel $x$ appartenant à $E$ et tout entier naturel $y$ appartenant à $E$, si $y \equiv 4x + 3$ modulo 27 alors $x \equiv 7y + 6$ modulo 27. En déduire que deux caractères distincts sont codés par deux caractères distincts.
- Proposer une méthode de décodage.
- Décoder le mot «$vfv$ ».
Spécialité 5 points
On note $E$ l'ensemble des vingt-sept nombres entiers compris entre $0$ et $26$.
On note $A$ l'ensemble dont les éléments sont les vingt-six lettres de l'alphabet et un séparateur entre deux mots, noté «$\star$ » considéré comme un caractère.
Pour coder les éléments de $A$, on procède de la façon suivante :
Premièrement : On associe à chacune des lettres de l'alphabet, rangées par ordre alphabétique, un nombre entier naturel compris entre 0 et 25, rangés par ordre croissant. On a donc $a \to 0,\: b \to 1, \ldots z \to 25$.
On associe au séparateur «$\star$ » le nombre 26.
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline a&b&c&d&e&f&g&h&i&j&k&l&m&n\\ \hline 0&1&2&3&4&5&6&7&8&9&10&11&12&13\\ \hline \end{array}$$
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline o&p&q&r&s&t&u&v&w&x&y&z&\star \\ \hline 14&15&13&17&18&19&20&21&22&23&24&25&26 \\ \hline \end{array}$$
On dit que $a$ a pour rang $0, b$ a pour rang 1, ... , $z$ a pour rang $25$ et le séparateur «$\star$ » a pour rang $26$.
Deuxièmement : à chaque élément $x$ de $E$, l'application $g$ associe le reste de la division euclidienne de $4x + 3$ par $27$.
On remarquera que pour tout $x$ de $E,\: g(x)$ appartient à $E$.
Troisièmement : Le caractère initial est alors remplacé par le caractère de rang $g(x)$. Exemple : $s \to 18, \quad g(18) = 21$ et $21 \to v$. Donc la lettre $s$ est remplacée lors du codage par la lettre $v$.
- Trouver tous les entiers $x$ de $E$ tels que $g(x) = x$ c'est-à-dire invariants par $g$.
En déduire les caractères invariants dans ce codage. On cherche les valeurs de $x$ telles que $4x+3 \equiv x [27]$. - Démontrer que, pour tout entier naturel $x$ appartenant à $E$ et tout entier naturel $y$ appartenant à $E$, si $y \equiv 4x + 3$ modulo 27 alors $x \equiv 7y + 6$ modulo 27. En déduire que deux caractères distincts sont codés par deux caractères distincts. Si $u \equiv 4x + 3 [27]$ alors$ 7y+6 \equiv 28x + 21 + 6 [27] \equiv 28x [27] \equiv x[27]$
- Proposer une méthode de décodage. Pour décoder un caractère $y$ il suffit de calculer $7y+6$ modulo $27$.
- Décoder le mot «$vfv$ ». $v$ est codé par $21$ et $f$ est codé par $5$.
$\Leftrightarrow 3x + 3 \equiv 0 [27]$
$\Leftrightarrow 3(x + 1) \equiv 0 [27]$
$\Leftrightarrow$ il existe $k\in \mathbb Z$ tel que $3(x+1) = 27k$
$\Leftrightarrow$ il existe $k\in \mathbb Z$ tel que $x+1 = 9k$
$\Leftrightarrow$ il existe $k\in \mathbb Z$ tel que $x = 9k – 1$
$\Leftrightarrow x \in \{8;17;26\}$
Les seuls caractères invariants sont donc $i$, $r$ et $\star$
Considérons $2$ caractères distincts codés par les nombres $x$ et $z$.
On sait que $0 \le x \le 26$ et $0 \le z \le 26$.
Si $g(x) = g(z) = y$ alors $x \equiv 7y +6 [27]$ et $z \equiv 7y+6$ et par conséquent $x \equiv z [27]$.
Ce qui est impossible puisque les caractères étaient distincts.
Donc $2$ caractères distincts sont codés par $2$ caractères distincts.
$7 \times 21 + 6 = 153 \equiv 18 [27]$ : caratère $s$
$7 \times 5 + 6 = 41 \equiv 14 [27]$ : caractère $o$
Par conséquent $vfv$ est décodé en $sos$.
$$\begin{array}{|c|c|c|}\hline &A&B\\ \hline 1&d &P(X \leq d)\\ \hline 2&0 &3,06E-138\\ \hline 3&1 &2,08E-112\\ \hline 4&2 &2,75E-89\\ \hline 5&3 &7,16E-69\\ \hline 6&4 &3,67E-51\\ \hline 7&5 &3,73E-36\\ \hline 8&6 &7,62E-24\\ \hline 9&7 &3,19E-14\\ \hline 10&8 &2,87E-07\\ \hline 11&9 &0,00620967\\ \hline 12&10 &0,5\\ \hline 13&11 &0,99379034\\ \hline 14&12 & 0,99999971\\ \hline 15&13 &1\\ \hline 16&14 & 1\\ \hline 17&15 &1\\ \hline 18&16 &1 \\ \hline 19&17 &1\\ \hline 20&18 &1\\ \hline 21&19 &1\\ \hline 22&20 &1\\ \hline 23&21 &1\\ \hline 24&22 &1\\ \hline 25& &\\ \hline \end{array}$$
Copie d'écran d'une feuille de calcul
- Vues: 57513
