Baccalauréat S Centres étrangers 13 juin 2019 - Correction Exercice 3
Page 6 sur 10
Correction de l'exercice 3 (5 points)
Le plan est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. Le but de cet exercice est de déterminer les nombres complexes $z$ non nuls tels que les points d'affixes 1, $z^2$ et $\dfrac{1}{z}$ soient alignés. Sur le graphique fourni en annexe, le point A a pour affixe 1.
Partie A: étude d'exemples
- Un premier exemple
Dans cette question, on pose $z = \text{i}$.- Donner la forme algébrique des nombres complexes $z^2$ et $\dfrac{1}{z}$. $z^2=\text{i} ^2=-1$
- $\dfrac{1}{z}=\dfrac{1}{\text{i} }=\dfrac{1}{\text{i} }\times \dfrac{\text{i} }{\text{i} }=\dfrac{\text{i} }{-1}=-\text{i} $.
- $\quad$
- Placer les points $N_1$ d'affixe $z^2$, et $P_1$ d'affixe $\dfrac{1}{z}$ sur le graphique donné en annexe. On remarque que dans ce cas les points A, $N_1$ et $P_1$ ne sont pas alignés.
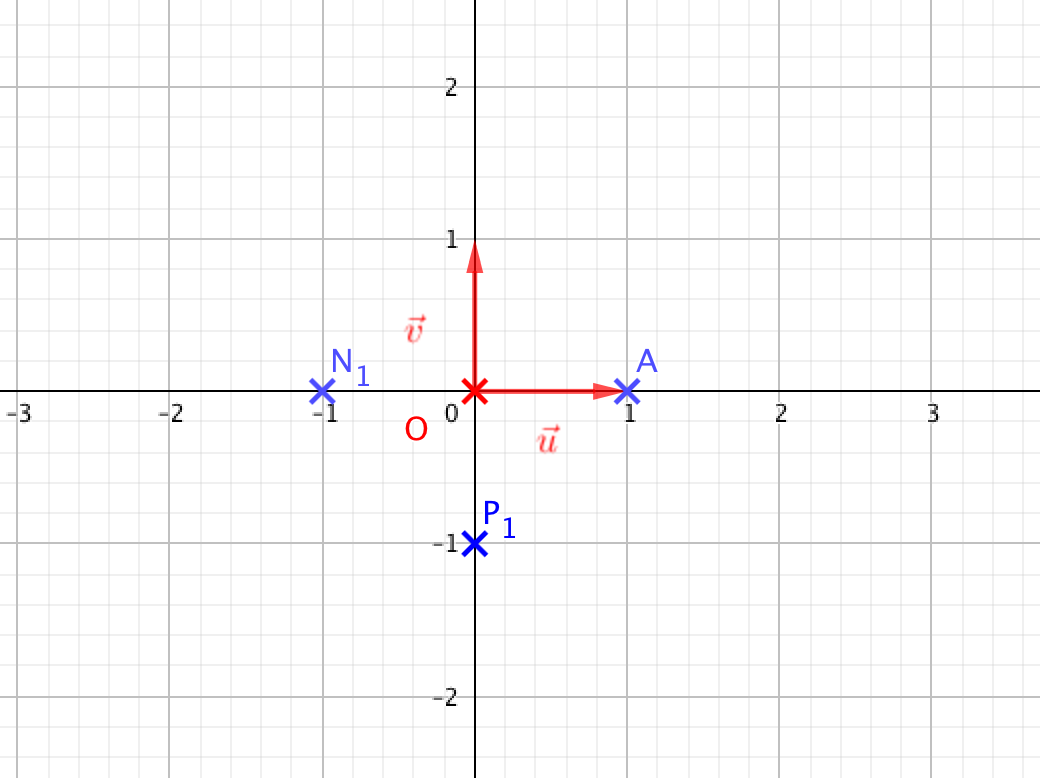
- L’affixe du vecteur $\vec{AN_1}$ est $z_{\vec{AN_1}}=-2$ et celle du vecteur $\vec{AP_1}$ est $z_{\vec{AP_1}}=-\text{i} -1$.
- Ces deux vecteurs ne sont clairement pas colinéaires et les points $A, N_1$ et $P_1$ ne sont pas alignés.
- $\quad$
- Une équation
Résoudre dans l'ensemble des nombres complexes l'équation d’inconnue $z$ : $z^2 + z + 1 = 0$.
On a l’équation $z^2+z+1=0$
- $\Delta=1^2-4\times 1\times 1=-3<0$.
- Les solutions de cette équation sont donc $z_1=\dfrac{-1-\text{i} \sqrt{3}}{2}$ et $z_2=\dfrac{-1+\text{i} \sqrt{3}}{2}$.
- $\quad$
- Un deuxième exemple
Dans cette question, on pose : $z = - \dfrac{1}{2} + \text{i}\dfrac{\sqrt{3}}{2}$.- Déterminer la forme exponentielle de $z$, puis celles des nombres complexes $z^2$ et $\dfrac{1}{z}$. On a $|z|=\left|-\dfrac{1}{2}+\text{i} \dfrac{\sqrt{3}}{2}\right|=1$
- Donc $z=\text{e}^{2\text{i} \pi/3} $
- $\quad$
- Ainsi $z^2=\text{e}^{2\times 2\text{i} \pi/3}=\text{e}^{4\text{i} \pi/3}$
- et $\dfrac{1}{z}=\text{e}^{-2\text{i} \pi/3}$.
- $\quad$
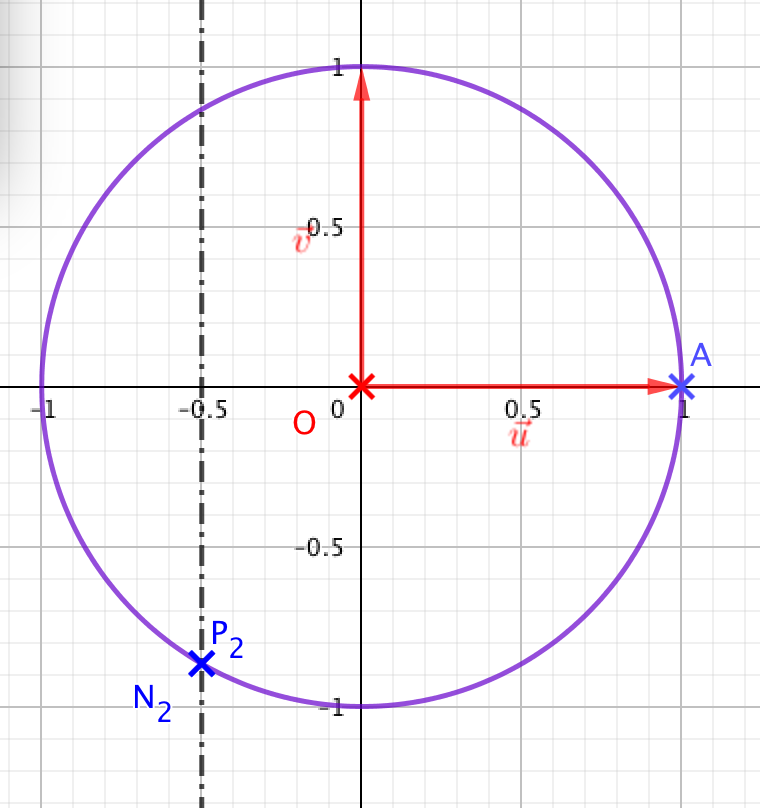
- Placer les points $N_2$ d'affixe $z^2$ et $P_2$, d’affixe $\dfrac{1}{z}$ sur le graphique donné en annexe. On remarque que dans, ce cas les points A, $N_2$ et $P_2$ sont alignés. On obtient le graphique suivant :
- $\quad$
- $z^2=\text{e}^{4\text{i} \pi/3}=\text{e}^{4\text{i} \pi/3-2\pi}=\text{e}^{-2\text{i} \pi/3}=\dfrac{1}{z}$.
- Les points $N_2$ et $P_2$ sont confondus.
- Par conséquent, les points $A, N_2$ et $P_2$ sont alignés.
- $\quad$
Partie B
Soit $z$ un nombre complexe non nul. On note $N$ le point d’affixe $z^2$ et $P$ le point d’affixe $\dfrac{1}{z}$.
- Établir que, pour tout nombre complexe différent de $0$, on a : \[z^2 - \dfrac{1}{z} = \left(z^2 + z + 1 \right)\left(1 - \dfrac{1}{z} \right).\] Pour tout nombre $z$ différent de $0$ on a :
- $\begin{align*} \left(z^2+z+1\right)\left(1-\dfrac{1}{z}\right) &=z^2-z+z-1+1-\dfrac{1}{z} \\
- &=z^2-\dfrac{1}{z}\end{align*}$
- On rappelle que si, $\vec{U}$ est un vecteur non nul et $\vec{V}$ un vecteur d’affixes respectives $z_{\vec{U}}$ et $z_{\vec{V}}$, les vecteurs $\vec{U}$ et $\vec{V}$ sont colinéaires si et seulement si il existe un nombre réel $k$ tel que $z_{\vec{V}} = k z_{\vec{U}}$. En déduire que, pour $z \ne 0$, les points A, $N$ et $P$ définis ci-dessus sont alignés si et seulement si $z^2 + z + 1$ est un réel. On considère un nombre complexe $z$ non nul.
- $\quad$
- L’affixe du vecteur $\vec{PN}$ est $z^2-\dfrac{1}{z}$.
- L’affixe du vecteur $\vec{PA}$ est $1-\dfrac{1}{z}$.
- Ces deux vecteurs sont colinéaires si, et seulement si, il existe un réel $k$ tel que $z^2-\dfrac{1}{z}=k\left(1-\dfrac{1}{z}\right)$.
- $\iff \left(z^2+z+1\right)\left(1-\dfrac{1}{z}\right) =k\left(1-\dfrac{1}{z}\right)$
- $\iff z^2+z+1=k$ ou $z=1$
- $\iff z^2+z+1\in \mathbb R$ ou $z=1$
- $\iff z^2+z+1\in \mathbb R$ (en effet si $z=1$ alors $z^2+z+1=3 \in \mathbb R)$.
- On pose $z = x+ \text{i}y$, où $x$ et $y$ désignent des nombres réels. Justifier que : $z^2 + z + 1 = x^2 - y^2 + x + 1 + \text{i} (2xy + y)$. Soient $x$ et $y$ des nombres réels et $z=x+\text{i} y$.
- $\quad$
- $\begin{align*} z^2+z+1&=(x+\text{i} y)^2+x+\text{i} y+1 \\
- &=x^2+2\text{i} xy-y^2+x+\text{i} y+1\\
- &=x^2-y^2+x+1+\text{i} (2xy+y)\end{align*}$
- $\quad$
-
- Déterminer l'ensemble des points $M$ d'affixe $z \ne 0$ tels que les points A, $N$ et $P$ soient alignés. $z^2+z+1$ est un réel si, et seulement si, $2xy+y=0$
- si, et seulement si, $y(2x+1)=0$
- si, et seulement si, $y=0$ ou $2x+1=0$
- si, et seulement si, $y=0$ ou $x=-\dfrac{1}{2}$
- Parmi cet ensemble de solutions, cherchons celles qui annulent également la partie réelle.
- – Si $y=0$ alors on cherche les solutions de l’équation $x^2+x+1=0$. D’après la question
- elle ne possède pas de solution réelle.
- – Si $x=-\dfrac{1}{2}$ alors on cherche les solutions de l’équation $\dfrac{1}{4}-y^2-\dfrac{1}{2}+1=0$ soit $y^2=\dfrac{3}{4}$. Cette équation possède deux solutions : $-\dfrac{\sqrt{3}}{2}$ et $\dfrac{\sqrt{3}}{2}$
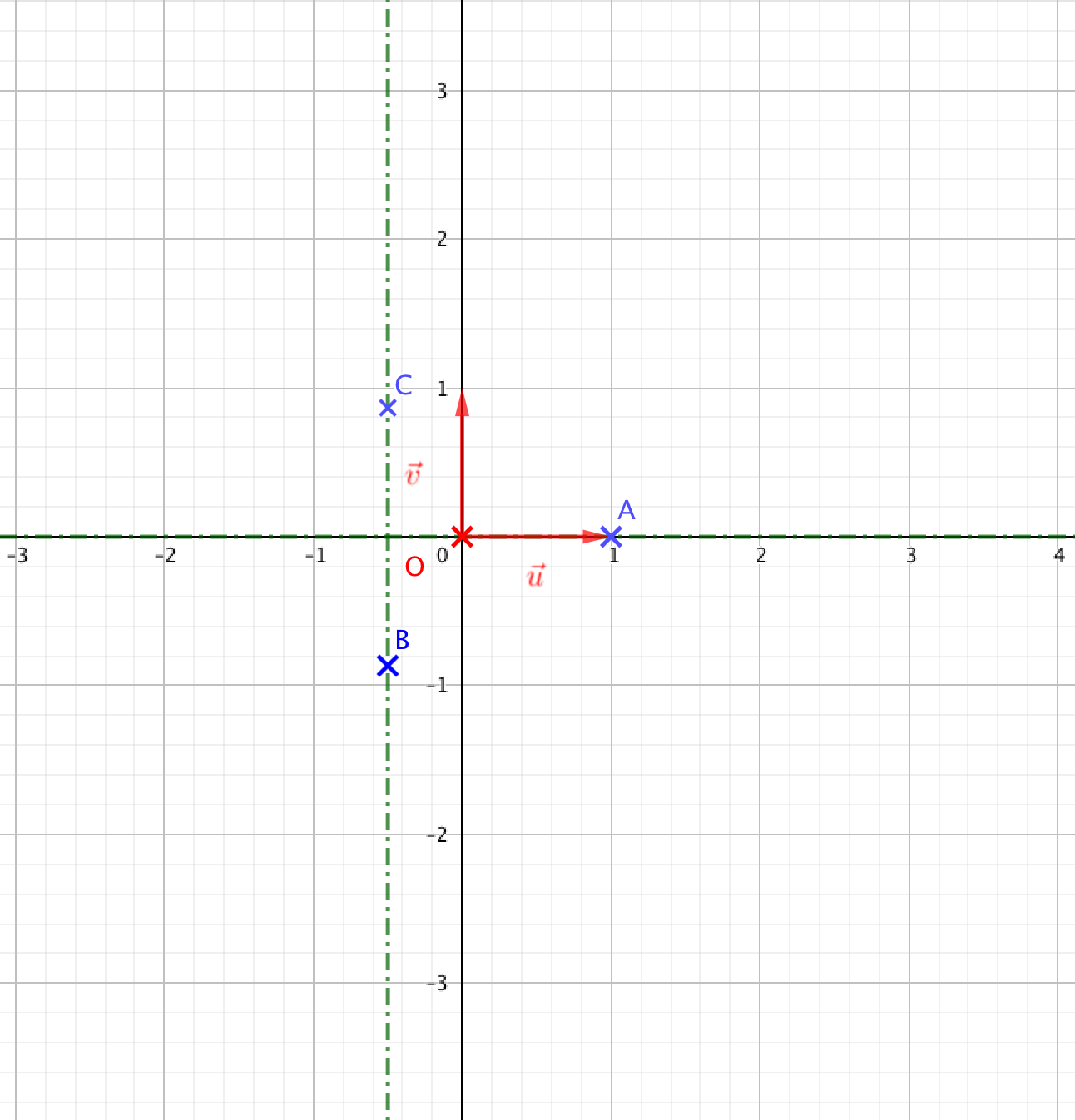
- Ainsi l’ensemble cherché la réunion des droites d’équation $y=0$ (l’axe des abscisses) et $x=-\dfrac{1}{2}$ privé des points $B$ et $C$ de coordonnées respectives $\left(-\dfrac{1}{2};-\dfrac{\sqrt{3}}{2}\right)$ et $\left(-\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)$.
- Tracer cet ensemble de points sur le graphique donné en annexe.
- Vues: 65574
