Baccalauréat S Amérique du Nord 28 mai 2019
Exercice 1 5 points
Dans cet exercice et sauf mention contraire, les résultats seront arrondis à $10^{-3}$.
Une usine fabrique des tubes.
Partie A
Les questions 1. et 2 . sont indépendantes.
On s'intéresse à deux types de tubes, appelés tubes de type 1 et tubes de type 2.
- Un tube de type 1 est accepté au contrôle si son épaisseur est comprise entre $1,35$ millimètre et $1,65$ millimètre.
- On désigne par $X$ la variable aléatoire qui, à chaque tube de type 1 prélevé au hasard dans la production d'une journée, associe son épaisseur exprimée en millimètres. On suppose que la variable aléatoire $X$ suit la loi normale d'espérance $1,5$ et d'écart-type $0,07$.
On prélève au hasard un tube de type 1 dans la production de la journée. Calculer la probabilité que le tube soit accepté au contrôle. - L'entreprise désire améliorer la qualité de la production des tubes de type 1. Pour cela, on modifie le réglage des machines produisant ces tubes. On note $X_1$ la variable aléatoire qui, à chaque tube de type 1 prélevé dans la production issue de la machine modifiée, associe son épaisseur. On suppose que la variable aléatoire $X_1$ suit une loi normale d'espérance $1,5$ et d'écart-type $\sigma_1$.
Un tube de type 1 est prélevé au hasard dans la production issue de la machine modifiée. Déterminer une valeur approchée à $10^{-3}$ près de $\sigma_1$ pour que la probabilité que ce tube soit accepté au contrôle soit égale à 0,98. (On pourra utiliser la variable aléatoire $Z$ définie par $Z = \dfrac{X_1 - 1,5}{\sigma_1}$ qui suit la loi normale centrée réduite.)
- On désigne par $X$ la variable aléatoire qui, à chaque tube de type 1 prélevé au hasard dans la production d'une journée, associe son épaisseur exprimée en millimètres. On suppose que la variable aléatoire $X$ suit la loi normale d'espérance $1,5$ et d'écart-type $0,07$.
- Une machine produit des tubes de type 2. Un tube de type 2 est dit « conforme pour la longueur » lorsque celle-ci, en millimètres, appartient à l’intervalle $[298~;~302]$. Le cahier des charges établit que, dans la production de tubes de type 2, une proportion de 2% de tubes non « conformes pour la longueur» est acceptable.
On souhaite décider si la machine de production doit être révisée. Pour cela, on prélève au hasard dans la production de tubes de type 2 un échantillon de $250$ tubes dans lequel 10 tubes se révèlent être non « conformes pour la longueur» .- Donner un intervalle de fluctuation asymptotique à $95$ % de la fréquence des tubes non « conformes pour la longueur» dans un échantillon de $250$ tubes.
- Décide-t-on de réviser la machine ? Justifier la réponse.
Partie B
Des erreurs de réglage dans la chaine de production peuvent affecter l'épaisseur ou la longueur des tubes de type 2. Une étude menée sur la production a permis de constater que :
- 96% des tubes de type 2 ont une épaisseur conforme;
- parmi les tubes de type 2 qui ont une épaisseur conforme, 95% ont une longueur conforme;
- 3,6% des tubes de type 2 ont une épaisseur non conforme et une longueur conforme.
On choisit un tube de type 2 au hasard dans la production et on considère les événements :
- $E$ : « l'épaisseur du tube est conforme» ;
- $L$ : « la longueur du tube est conforme» .
On modélise l'expérience aléatoire par un arbre pondéré : 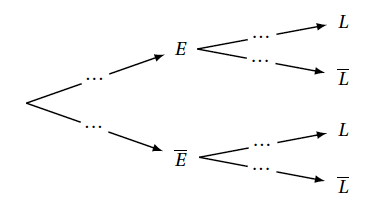
- Recopier et compléter entièrement cet arbre.
- Montrer que la probabilité de l'événement $L$ est égale à 0,948.
Correction de l'exercice 1 (5 points)
Dans cet exercice et sauf mention contraire, les résultats seront arrondis à $10^{-3}$.
Une usine fabrique des tubes.
Partie A
Les questions 1. et 2 . sont indépendantes.
On s'intéresse à deux types de tubes, appelés tubes de type 1 et tubes de type 2.
- Un tube de type 1 est accepté au contrôle si son épaisseur est comprise entre $1,35$ millimètre et $1,65$ millimètre.
- On désigne par $X$ la variable aléatoire qui, à chaque tube de type 1 prélevé au hasard dans la production d'une journée, associe son épaisseur exprimée en millimètres. On suppose que la variable aléatoire $X$ suit la loi normale d'espérance $1,5$ et d'écart-type $0,07$.
On prélève au hasard un tube de type 1 dans la production de la journée. Calculer la probabilité que le tube soit accepté au contrôle. On veut calculer $P(1,35\leq X\leq 1,65)$. - L'entreprise désire améliorer la qualité de la production des tubes de type 1. Pour cela, on modifie le réglage des machines produisant ces tubes. On note $X_1$ la variable aléatoire qui, à chaque tube de type 1 prélevé dans la production issue de la machine modifiée, associe son épaisseur. On suppose que la variable aléatoire $X_1$ suit une loi normale d'espérance $1,5$ et d'écart-type $\sigma_1$.
Un tube de type 1 est prélevé au hasard dans la production issue de la machine modifiée. Déterminer une valeur approchée à $10^{-3}$ près de $\sigma_1$ pour que la probabilité que ce tube soit accepté au contrôle soit égale à 0,98. (On pourra utiliser la variable aléatoire $Z$ définie par $Z = \dfrac{X_1 - 1,5}{\sigma_1}$ qui suit la loi normale centrée réduite.) La variable $Z=\dfrac{X_1-1,5}{\sigma_1}$ suit la loi normale centrée réduite.
D’après la calculatrice on trouve $P(1,35\leq X\leq 1,65)\approx 0,968$.
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$
On a
$\begin{align*} P\left(1,35\leq X_1\leq 1,65\right)=0,98 &\iff P\left(-0,15 \leq X_1-1,5\leq 0,15\right)=0,98 \\
&\iff P\left(-\dfrac{0,15}{\sigma_1} \leq \dfrac{X_1-1,5}{\sigma_1}\leq \dfrac{0,15}{\sigma_1}\right)=0,98 \\
&\iff P\left(-\dfrac{0,15}{\sigma_1} \leq Z\leq \dfrac{0,15}{\sigma_1}\right)=0,98 \\
&\iff 2P\left(Z\leq \dfrac{0,15}{\sigma_1}\right)-1=0,98\quad\text{(propriété du cours)}\\
&\iff 2P\left(Z\leq \dfrac{0,15}{\sigma_1}\right)=1,98 \\
&\iff P\left(Z\leq \dfrac{0,15}{\sigma_1}\right)=0,99\end{align*}$
À l’aide de la touche Inverse loi normale de la calculatrice, on trouve $\dfrac{0,15}{\sigma_1} \approx 2,326$ et donc $\sigma_1 \approx 0,064$.
$\quad$ - On désigne par $X$ la variable aléatoire qui, à chaque tube de type 1 prélevé au hasard dans la production d'une journée, associe son épaisseur exprimée en millimètres. On suppose que la variable aléatoire $X$ suit la loi normale d'espérance $1,5$ et d'écart-type $0,07$.
On souhaite décider si la machine de production doit être révisée. Pour cela, on prélève au hasard dans la production de tubes de type 2 un échantillon de $250$ tubes dans lequel 10 tubes se révèlent être non « conformes pour la longueur» .
- Donner un intervalle de fluctuation asymptotique à $95$ % de la fréquence des tubes non « conformes pour la longueur» dans un échantillon de $250$ tubes. On a $n=250$ et $p=0,02$.
- Décide-t-on de réviser la machine ? Justifier la réponse. La fréquence observée est $f=\dfrac{10}{250}=0,04\notin I_{250}$.
Donc $n\geq 30$, $np=5\geq 5$ et $n(1-p)=245\geq 5$.
Un intervalle de fluctuation asymptotique à $95\%$ de la fréquence des tubes non « conformes pour la longueur » est :
$\begin{align*} I_{250}&=\left[0,02-1,96\sqrt{\dfrac{0,02\times 0,98}{250}};0,02+1,96\sqrt{\dfrac{0,02\times 0,98}{250}}\right] \\
&\approx [0,002;0,038]\end{align*}$
$\quad$
Au risque d’erreur de $5\%$, il faut réviser la machine.
Partie B
Des erreurs de réglage dans la chaine de production peuvent affecter l'épaisseur ou la longueur des tubes de type 2. Une étude menée sur la production a permis de constater que :
- 96% des tubes de type 2 ont une épaisseur conforme;
- parmi les tubes de type 2 qui ont une épaisseur conforme, 95% ont une longueur conforme;
- 3,6% des tubes de type 2 ont une épaisseur non conforme et une longueur conforme.
On choisit un tube de type 2 au hasard dans la production et on considère les événements :
- $E$ : « l'épaisseur du tube est conforme» ;
- $L$ : « la longueur du tube est conforme» .
On modélise l'expérience aléatoire par un arbre pondéré : 
- Recopier et compléter entièrement cet arbre.
- Montrer que la probabilité de l'événement $L$ est égale à 0,948. D’après la formule des probabilités totales on a :
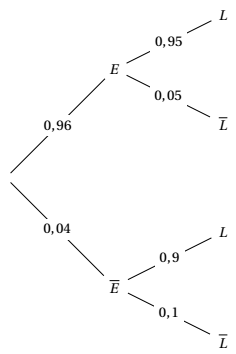
$\begin{align*} P(L)&=P(E\cap L)+P\left(\overline{E}\cap L\right) \\
&=0,96\times 0,95+0,036 \\
&=0,948\end{align*}$
$\quad$
Exercice 2 4 points
Le plan complexe est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. Dans ce qui suit, $z$ désigne un nombre complexe.
Pour chacune des affirmations ci-dessous, indiquer sur la copie si elle est vraie ou si elle est fausse. Justifier. Toute réponse non justifiée ne rapporte aucun point.
- Affirmation 1 : L'équation $z - \text{i} = \text{i}(z + 1)$ a pour solution $\sqrt{2}\text{e}^{\text{i}\frac{\pi}{4}}$.
- Affirmation 2 : Pour tout réel $x \in \left] -\dfrac{\pi}{2}~;~\dfrac{\pi}{2} \right[$, le nombre complexe $1 + \text{e}^{2\text{i} x}$ admet pour forme exponentielle $2 \cos x \text{e}^{-\text{i}x}$.
- Affirmation 3 : Un point M d'affixe $z$ tel que $\big|z - \text{i}\big| = \big|z + 1\big|$ appartient à la droite d'équation $y = -x$.
- Affirmation 4 : L'équation $z^5 + z - \text{i} + 1 = 0$ admet une solution réelle.
Correction de l'exercice 2 (4 points)
Le plan complexe est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. Dans ce qui suit, $z$ désigne un nombre complexe.
Pour chacune des affirmations ci-dessous, indiquer sur la copie si elle est vraie ou si elle est fausse. Justifier. Toute réponse non justifiée ne rapporte aucun point.
- Affirmation 1 : L'équation $z - \text{i} = \text{i}(z + 1)$ a pour solution $\sqrt{2}\text{e}^{\text{i}\frac{\pi}{4}}$. Affirmation 1 fausse
- Affirmation 2 : Pour tout réel $x \in \left] -\dfrac{\pi}{2}~;~\dfrac{\pi}{2} \right[$, le nombre complexe $1 + \text{e}^{2\text{i} x}$ admet pour forme exponentielle $2 \cos x \text{e}^{-\text{i}x}$.
- Affirmation 3 : Un point M d'affixe $z$ tel que $\big|z - \text{i}\big| = \big|z + 1\big|$ appartient à la droite d'équation $y = -x$.
- Affirmation 4 : L'équation $z^5 + z - \text{i} + 1 = 0$ admet une solution réelle.
$\begin{align*} z-\text{i}=i(z+1)&\iff z-\text{i}=\text{i} z+\text{i} \\
&\iff z-\text{i} z=2\text{i} \\
&\iff z(1-\text{i})=2\text{i} \\
&\iff z=\dfrac{2\text{i}}{1-\text{i}}\end{align*}$
Or $2\text{i}=2\text{e}^{\text{i} \pi/2}$
et $|1-\text{i}|=\sqrt{2}$ donc $|1-\text{i}|=\sqrt{2}\left(\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}\right)=\sqrt{2}\text{e}^{-\text{i} \pi/4}$
Par conséquent :
$\begin{align*} z-\text{i}=i(z+1)&\iff z=\dfrac{2\text{e}^{\text{i} \pi/2}}{\sqrt{2}\text{e}^{-\text{i} \pi/4}} \\
&\iff =\sqrt{2}\text{e}^{3\text{i}\pi/4}\end{align*}$
Or $\sqrt{2}\text{e}^{3\text{i}\pi/4}\neq \sqrt{2}\text{e}^{\text{i}\pi/4}$.
$\quad$
Affirmation 2 fausse
Pour tout réel $x\in \left]-\dfrac{\pi}{2};\dfrac{\pi}{2}\right[$ on a :
$\begin{align*} 2\cos x\text{e}^{-\text{i} x}&=2\times \dfrac{\text{e}^{\text{i} x}+\text{e}^{-\text{i} x}}{2}\times \text{e}^{-\text{i} x} \\
&=1+\text{e}^{-2\text{i} x} \\
&=\overline{1+\text{e}^{2\text{i} x}} \end{align*}$
Or , sur l’intervalle $\left]-\dfrac{\pi}{2};\dfrac{\pi}{2}\right[$ on a $1+\text{e}^{2\text{i} x} \neq \overline{1+\text{e}^{2\text{i} x}} $ sauf si $x=0$ (seule valeur pour laquelle l’exponentielle complexe est un réel).
$\quad$
Affirmation 3 vraie
On appelle $A$ le point d’affixe $\text{i}$ et $B$ le point d’affixe $-1$.
Ainsi : $|z-\text{i}|=|z+1|\iff AM=BM$
Le point $M$ appartient donc à la médiatrice du segment $[AB]$.
On appelle $D$ le point d’affixe $-1+\text{i}$.
Ainsi le quadrilatère $OBDA$ est un carré dont les diagonales sont $[OD]$ et $[AB]$.
Dans un carré, les diagonales sont perpendiculaires et une équation de la droite $(OD)$ est $y=-x$.
Par conséquent le point $M$ appartient à la droite d’équation $y=-x$.
$\quad$
Affirmation 4 fausse
Supposons que l’équation $z^5+z-\text{i}+1=0$ possède une solution réelle $z_0$.
On a alors ${z_0}^5+z_0+1=\text{i}$
Cela signifie que $\text{i}$ est un réel ce qui est absurde. La supposition faite est donc impossible.
$\quad$
Exercice 3 6 points
Partie A : établir une inégalité
Sur l'intervalle $[0~;~ +\infty[$, on définit la fonction $f$ par $f(x) = x - \ln(x + 1)$.
- Étudier le sens de variation de la fonction $f$ sur l'intervalle $[0~;~ +\infty[$.
- En déduire que pour tout $x \in [0~;~ +\infty[, \quad \ln(x + 1) \leqslant x$.
Partie B : application à l'étude d'une suite
On pose $u_0 = 1$ et pour tout entier naturel $n$, $u_{n+1} = u_n - \ln(1 + u_n)$. On admet que la suite de terme général $u_n$ est bien définie.
- Calculer une valeur approchée à $10^{-3}$ près de $u_2$.
-
- Démontrer par récurrence que pour tout entier naturel $n, \quad u_n \geqslant 0$.
- Démontrer que la suite $(u_n)$ est décroissante, et en déduire que pour tout entier naturel $n, \quad u_n \leqslant 1 $.
- Montrer que la suite $(u_n)$ est convergente.
- On note $\ell$ la limite de la suite $(u_n)$ et on admet que $\ell = f(\ell)$, où $f$ est la fonction définie dans la Partie A . En déduire la valeur de $\ell$.
-
- Écrire un algorithme qui, pour un entier naturel $p$ donné, permet de déterminer le plus petit rang $N$ à partir duquel tous les termes de la suite $\left(u_n\right)$ sont inférieurs à $10^{-p}$.
- Déterminer le plus petit entier naturel $n$ à partir duquel tous les termes de la suite $\left(u_n\right)$ sont inférieurs à $10^{-15}$.
Correction de l'exercice 3 (5 points)
Partie A : établir une inégalité
Sur l'intervalle $[0~;~ +\infty[$, on définit la fonction $f$ par $f(x) = x - \ln(x + 1)$.
- Étudier le sens de variation de la fonction $f$ sur l'intervalle $[0~;~ +\infty[$. i>La fonction $f$ est dérivable sur l’intervalle $[0;+\infty[$ en tant que somme de fonctions dérivables sur cet intervalle.
- En déduire que pour tout $x \in [0~;~ +\infty[, \quad \ln(x + 1) \leqslant x$. De plus $f(0)=0-\ln(1)=0$.
Pour tout réel $x\in[0;+\infty[$ on a :
$f'(x)=1-\dfrac{1}{x+1}=\dfrac{x+1-1}{x+1}=\dfrac{x}{x+1}$
Sur l’intervalle $[0;+\infty[$ on a $x\geq 0$ et $x+1>0$.
Par conséquent $f(x)\geq 0$ et la fonction $f$ est strictement croissante sur cet intervalle.
$\quad$
Pour tout réel $x\in [0;+\infty[$ on a, d’après la question précédente : $0\leq f(0)\leq f(x)$
Donc $0\leq x-\ln(x+1) \iff \ln(x+1)\leq x$.
$\quad$
Partie B : application à l'étude d'une suite
On pose $u_0 = 1$ et pour tout entier naturel $n$, $u_{n+1} = u_n - \ln(1 + u_n)$. On admet que la suite de terme général $u_n$ est bien définie.
- Calculer une valeur approchée à $10^{-3}$ près de $u_2$. On a $u_1=1-\ln(2)$
-
- Démontrer par récurrence que pour tout entier naturel $n, \quad u_n \geqslant 0$. Initialisation : Si $n=0$ alors $u_0=1\geq 0$.
- Démontrer que la suite $(u_n)$ est décroissante, et en déduire que pour tout entier naturel $n, \quad u_n \leqslant 1 $. Pour tout entier naturel $n$ on a :
- Montrer que la suite $(u_n)$ est convergente. La suite $\left(u_n\right)$ est décroissante et minorée par $0$; elle est donc convergente.
La propriété est vraie au rang $0$.
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$, donc $u_n\geq 0$.
Montrons que la propriété est encore vraie au rang $n+1$, c’est-à-dire que $u_n-\ln\left(1+u_n\right) \geq 0$.
On a $u_{n+1}=f\left(u_n\right)$.
D’après la question A.2. on sait que pour tout réel $x$ on a $f(x) \geq 0$.
Puisque $u_n\geq 0$ on a donc $f\left(u_n\right) \geq 0$.
La propriété est ainsi vraie au rang $n+1$.
$\quad$
Conclusion : la propriété est vraie au rang $0$ et est héréditaire.
Ainsi, pour tout entier naturel $n$, on a $u_n\geq 0$.
$\quad$
$u_{n+1}-u_n=-\ln\left(1+u_n\right)$
D’après la question précédente on a $u_n\geq 0$ donc $1+u_n\geq 1$ et $\ln\left(1+u_n\right) \geq 0$.
Ainsi $u_{n+1}-u_n\leq 0$
et la suite $\left(u_n\right)$ est décroissante.
$\quad$
La suite $\left(u_n\right)$ étant décroissante et $u_0=1$ on a donc, pour tout entier naturel $n$, $u_n\leq u_0$ soit $u_n\leq 1$.
$\quad$
$\quad$ - On note $\ell$ la limite de la suite $(u_n)$ et on admet que $\ell = f(\ell)$, où $f$ est la fonction définie dans la Partie A . En déduire la valeur de $\ell$. La limite $\ell$ est solution de l’équation :
-
- Écrire un algorithme qui, pour un entier naturel $p$ donné, permet de déterminer le plus petit rang $N$ à partir duquel tous les termes de la suite $\left(u_n\right)$ sont inférieurs à $10^{-p}$. On peut écrire l’algorithme suivant :
- Déterminer le plus petit entier naturel $n$ à partir duquel tous les termes de la suite $\left(u_n\right)$ sont inférieurs à $10^{-15}$. On a $u_5\approx 3,96\times 10^{-14}$ et $u_6\approx 4,942\times 10^{-17}$.
$$\begin{array}{|l|}
\hline
U\leftarrow 1 \\
N\leftarrow 0\\
\text{Tant que }U\geq 10^{-p} \\
\hspace{1cm} U\leftarrow U-\ln(1+U) \\
\hspace{1cm} N\leftarrow N+1\\
\text{Fin tant que}\\
\hline
\end{array}$$
$\quad$
Puisque la suite $\left(u_n\right)$ est décroissante, cela signifie qu’à partir du rang $6$ on a $u_n\leq 10^{-15}$.
$\quad$
Remarque : Sur certaines calculatrices(Casio graph75/90, TI83PCE, en particulier) la calculatrice reste “bloquée” sur environ $4,325\times 10^{-14}$ ou une autre valeur étrange. Pas de soucis avec la Numworks en revanche.
$\quad$
et $u_2=1-\ln(2)-\ln\left(2-\ln(2)\right)\approx 0,039$.
$\quad$
$\begin{align*} f(x)=x &\iff x-\ln(1+x)=x \\
&\iff -\ln(1+x)=0 \\
&\iff 1+x=1 \\
&\iff x=0\end{align*}$
Par conséquent $\ell =0$.
$\quad$
Exercice 4 5 points
On relie les centres de chaque face d'un cube ABCDEFGH pour former un solide IJKLMN comme sur la figure ci-dessous. 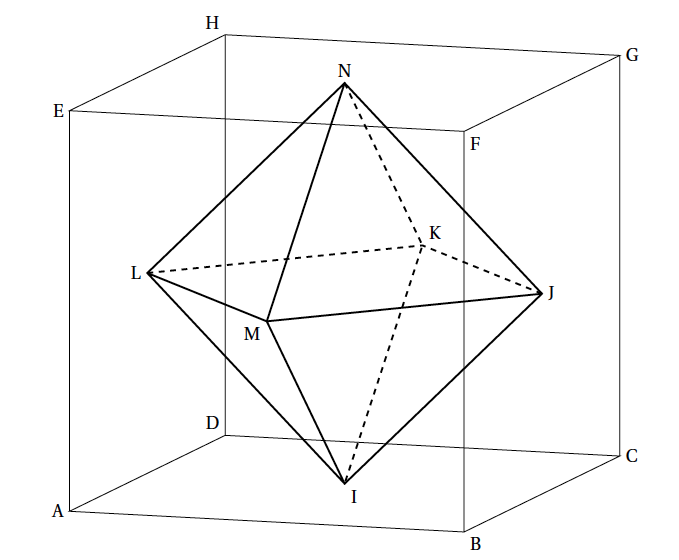
Plus précisément, les points I, J, K, L, M et N sont les centres respectifs des faces carrées ABCD, BCGF, CDHG, ADHE, ABFE et EFGH (donc les milieux des diagonales de ces carrés).
- Sans utiliser de repère (et donc de coordonnées) dans le raisonnement mené, justifier que les droites (IN) et (ML) sont orthogonales.
-
- Donner les coordonnées des vecteurs $ \vec{\text{NC}} $ et $ \vec{\text{ML}} $.
- En déduire que les droites (NC) et (ML) sont orthogonales.
- Déduire des questions précédentes une équation cartésienne du plan (NCI).
-
- Montrer qu'une équation cartésienne du plan (NJM) est : $x - y + z = 1 $.
- La droite (DF) est-elle perpendiculaire au plan (NJM)? Justifier.
- Montrer que l'intersection des plans (NJM) et (NCI) est une droite dont on donnera un point et un vecteur directeur. Nommer la droite ainsi obtenue en utilisant deux points de la figure.
Dans la suite, on considère le repère orthonormé $\left(\text{A}~;~\vec{\text{AB}}~;~\vec{\text{AD}}~;~\vec{\text{AE}}\right) $ dans lequel, par exemple, le point N a pour coordonnées $\left(\dfrac{1}{2}~;~\dfrac{1}{2}~;~1\right) $.
Correction de l'exercice 4 5 points
On relie les centres de chaque face d'un cube ABCDEFGH pour former un solide IJKLMN comme sur la figure ci-dessous. 
Plus précisément, les points I, J, K, L, M et N sont les centres respectifs des faces carrées ABCD, BCGF, CDHG, ADHE, ABFE et EFGH (donc les milieux des diagonales de ces carrés).
- Sans utiliser de repère (et donc de coordonnées) dans le raisonnement mené, justifier que les droites (IN) et (ML) sont orthogonales. Les plans $(ABC)$ et $(KLM)$ sont parallèles.
-
- Donner les coordonnées des vecteurs $ \vec{\text{NC}} $ et $ \vec{\text{ML}} $. On a $N(0,5;0,5;1)$ et $C(1;1;0)$
- En déduire que les droites (NC) et (ML) sont orthogonales. On a $\vec{NC}.\vec{ML}=-0,25+0,25+0=0$.
- Déduire des questions précédentes une équation cartésienne du plan (NCI). Le vecteur $\vec{ML}$ est donc aux vecteurs $\vec{IN}$ et $\vec{NC}$ qui sont deux vecteurs non colinéaires du plan $(NCI)$.
Le vecteur $\vec{NC}$ a donc pour coordonnées $(0,5;0,5;-1)$.
On a $M(0,5;0;0,5)$ et $L(0;0,5;0,5)$
Le vecteur $\vec{ML}$ a donc pour coordonnées $(-0,5;0,5;0)$.
$\quad$
Par conséquent les vecteurs $\vec{NC}$ et $\vec{ML}$ sont orthogonaux et les droites $(NC)$ et $(ML)$ sont orthogonales.
$\quad$
Une équation cartésienne de ce plan est alors de la forme $-0,5x+0,5y+d=0$.
Or $C(1;1;0)$ appartient à ce plan.
Par conséquent $0+0+d=0\iff d=0$.
Une équation cartésienne du plan $(NCI)$ est donc $-0,5x+0,5y=0$.
$\quad$ -
- Montrer qu'une équation cartésienne du plan (NJM) est : $x - y + z = 1 $. >On a :
- La droite (DF) est-elle perpendiculaire au plan (NJM)? Justifier. Un vecteur normal au plan $(NJM)$ est donc $\vec{n}(1;-1;1)$.
- Montrer que l'intersection des plans (NJM) et (NCI) est une droite dont on donnera un point et un vecteur directeur. Nommer la droite ainsi obtenue en utilisant deux points de la figure. On veut résoudre le système suivant :
$N(0,5;0,5;1)$ donc $0,5-0,5+1=0+1=1\checkmark$
$M(0,5;0;0,5)$ donc $0,5-0+0,5=1 \checkmark$
$J(1;0,5;0,5)$ donc $1-0,5+0,5=1+0=1\checkmark$
Les coordonnées de ces trois points vérifient l’équation $x-y+z=1$.
Ainsi une équation cartésienne du plan $(NJM)$ est bien $x-y+z=1$.
$\quad$
On a $D(0;1;0)$ et $F(1;0;1)$ donc $\vec{DF}(1;-1;1)$
Ainsi $\vec{n}$ et $\vec{DF}$ sont colinéaires et la droite $(DF)$ est perpendiculaire au plan $(NIM)$.
$\quad$
$\begin{cases} x-y+z=1\\-0,5x+0,5y=0 \end{cases} \iff \begin{cases} x=y\\x-y+z=1\end{cases} \iff \begin{cases} x=y\\z=1\end{cases}$
L’intersection des deux plans $(NJM)$ et $(NCI)$ est donc la droite dont une représentation paramétrique est $\begin{cases} x=t\\y=t\\z=1\end{cases} \quad, t\in \mathbb R$.
Cette droite passe donc par le point de coordonnées $(0;0;1)$ et a pour vecteur directeur le vecteur $\vec{u}(1;1;0)$.
Le point $N$ appartient à ces deux plans et le point $E$ a pour coordonnées $(0;0;1)$.
L’intersection des deux plans est donc la droite $(NE)$.
$\quad$
Les droites $(IN)$ et $(AE)$ sont parallèles et la droite $(AE)$ est perpendiculaire au plan $(ABC)$.
La droite $(IN)$ est par conséquent perpendiculaire au plan $(KLM)$. Elle est donc orthogonale à toutes les droites de ce plan, en particulier à la droite $(ML)$.
$\quad$
Dans la suite, on considère le repère orthonormé $\left(\text{A}~;~\vec{\text{AB}}~;~\vec{\text{AD}}~;~\vec{\text{AE}}\right) $ dans lequel, par exemple, le point N a pour coordonnées $\left(\dfrac{1}{2}~;~\dfrac{1}{2}~;~1\right) $.
Spécialité 5 points
Deux matrices colonnes $\begin{pmatrix} x\\y \end{pmatrix}$ et $\begin{pmatrix} x'\\y' \end{pmatrix}$ à coefficients entiers sont dites congrues modulo 5 si et seulement si $\left\{\begin{array}{l} x \equiv x'~[5]\\ y\equiv y'~[5] \end{array} \right.$.
Deux matrices carrées d'ordre 2 $\begin{pmatrix} a&c\\b&d \end{pmatrix}$ et $\begin{pmatrix} a'&c'\\b'&d' \end{pmatrix}$ à coefficients entiers sont dites congrues modulo 5 si et seulement si $\left\{\begin{array}{l} a \equiv a'~[5]\\ b\equiv b'~[5] \\c \equiv c'~[5]\\ d\equiv d'~[5] \end{array} \right.$.
Alice et Bob veulent s'échanger des messages en utilisant la procédure décrite ci-dessous.
- Ils choisissent une matrice M carrée d'ordre 2, à coefficients entiers.
- Leur message initial est écrit en lettres majuscules sans accent.
- Chaque lettre de ce message est remplacée par une matrice colonne $\begin{pmatrix} x\\y \end{pmatrix}$ déduite du tableau ci-contre : $x$ est le chiffre situé en haut de la colonne et $y$ est le chiffre situé à la gauche de la ligne; par exemple, la lettre $\textsf{T}$ d'un message initial correspond à la matrice colonne $\begin{pmatrix} 4\\3 \end{pmatrix}$.
- On calcule une nouvelle matrice $\begin{pmatrix} x'\\y' \end{pmatrix}$ en multipliant $\begin{pmatrix} x\\y \end{pmatrix}$ à gauche par la matrice M : $\begin{pmatrix} x'\\y' \end{pmatrix} = \text{M} \begin{pmatrix} x\\y \end{pmatrix}$.
- On calcule $r'$ et $t'$ les restes respectifs des divisions euclidiennes de $x'$ et $y'$ par 5.
$$\begin{array}{|c|c|c|c|c|c|}\hline & 0 &1 &2 &3 &4 \\ \hline 0 &\textsf{A} &\textsf{B}& \textsf{C} &\textsf{D} &\textsf{E} \\ \hline 1& \textsf{F} &\textsf{G} &\textsf{H} &\textsf{I}& \textsf{J} \\ \hline 2& \textsf{K} &\textsf{L} &\textsf{M}& \textsf{N}& \textsf{O} \\ \hline 3 & \textsf{P} &\textsf{Q} &\textsf{R} &\textsf{S} &\textsf{T}\\ \hline 4 & \textsf{U} &\textsf{V} &\textsf{X} &\textsf{Y}& \textsf{Z} \\ \hline \end{array}$$ Remarque : la lettre $\textsf{W}$ est remplacée par les deux lettres accolées $\textsf{V}$.
- On utilise le tableau ci-contre pour obtenir la nouvelle lettre correspondant à la matrice colonne $\begin{pmatrix} r'\\t' \end{pmatrix}$.
- Bob et Alice choisissent la matrice $\text{M} = \begin{pmatrix} 1&2\\3&4 \end{pmatrix}$.
- Montrer que la lettre « $\textsf{T}$» du message initial est codée par la lettre « $\textsf{U}$» puis coder le message « $\textsf{TE}$» .
- On pose $\text{P} = \begin{pmatrix} 3&1\\4&2 \end{pmatrix}$. Montrer que les matrices PM et $\text{I} = \begin{pmatrix} 1&0\\0&1 \end{pmatrix}$ sont congrues modulo 5.
- On considère A, A' deux matrices d'ordre 2 à coefficients entiers congrues modulo 5 et $\text{Z} =\begin{pmatrix} x\\y \end{pmatrix}$, $\text{Z}' =\begin{pmatrix} x'\\y' \end{pmatrix}$ deux matrices colonnes à coefficients entiers congrues modulo 5. Montrer alors que les matrices AZ et A'Z' sont congrues modulo 5.
Dans ce qui suit on admet que si A, A' sont deux matrices carrées d'ordre 2 à coefficients entiers congrues modulo 5 et si B, B' sont deux matrices carrées d'ordre 2 à coefficients entiers congrues modulo 5 alors les matrices produit AB et A'B' sont congrues modulo 5.
-
- On note $\text{X}= \begin{pmatrix} x_1\\x_2 \end{pmatrix}$ et $\text{Y} = \begin{pmatrix} y_1\\y_2 \end{pmatrix}$ deux matrices colonnes à coefficients entiers. Déduire des questions précédentes que si MX et Y sont congrues modulo 5 alors les matrices X et PY sont congrues modulo 5; ce qui permet de « décoder» une lettre chiffrée par la procédure utilisée par Alice et Bob avec la matrice M choisie.
- Décoder alors la lettre « $\textsf{D}$» .
- On souhaite déterminer si la matrice $\text{R}=\begin{pmatrix} 1&2\\4&3 \end{pmatrix}$ peut être utilisée pour coder un message.
- On pose $\text{S} = \begin{pmatrix} 2&2\\4&4 \end{pmatrix}$. Vérifier que la matrice RS et la matrice $\begin{pmatrix} 0&0\\0&0 \end{pmatrix}$ sont congrues modulo 5.
- On admet qu'un message codé par la matrice R peut être décodé s‘il existe une matrice T telle que les matrices TR et I soient congrues modulo 5. Montrer que si c‘est le cas alors les matrices TRS et S sont congrues modulo 5 (par la procédure expliquée en question \textbf{1. d.} pour le codage avec la matrice M).
- En déduire qu‘un message codé par la matrice R ne peut être décodé.
Correction de l'exercice de Spécialité 5 points
Deux matrices colonnes $\begin{pmatrix} x\\y \end{pmatrix}$ et $\begin{pmatrix} x'\\y' \end{pmatrix}$ à coefficients entiers sont dites congrues modulo 5 si et seulement si $\left\{\begin{array}{l} x \equiv x'~[5]\\ y\equiv y'~[5] \end{array} \right.$.
Deux matrices carrées d'ordre 2 $\begin{pmatrix} a&c\\b&d \end{pmatrix}$ et $\begin{pmatrix} a'&c'\\b'&d' \end{pmatrix}$ à coefficients entiers sont dites congrues modulo 5 si et seulement si $\left\{\begin{array}{l} a \equiv a'~[5]\\ b\equiv b'~[5] \\c \equiv c'~[5]\\ d\equiv d'~[5] \end{array} \right.$.
Alice et Bob veulent s'échanger des messages en utilisant la procédure décrite ci-dessous.
- Ils choisissent une matrice M carrée d'ordre 2, à coefficients entiers.
- Leur message initial est écrit en lettres majuscules sans accent.
- Chaque lettre de ce message est remplacée par une matrice colonne $\begin{pmatrix} x\\y \end{pmatrix}$ déduite du tableau ci-contre : $x$ est le chiffre situé en haut de la colonne et $y$ est le chiffre situé à la gauche de la ligne; par exemple, la lettre $\textsf{T}$ d'un message initial correspond à la matrice colonne $\begin{pmatrix} 4\\3 \end{pmatrix}$.
- On calcule une nouvelle matrice $\begin{pmatrix} x'\\y' \end{pmatrix}$ en multipliant $\begin{pmatrix} x\\y \end{pmatrix}$ à gauche par la matrice M : $\begin{pmatrix} x'\\y' \end{pmatrix} = \text{M} \begin{pmatrix} x\\y \end{pmatrix}$.
- On calcule $r'$ et $t'$ les restes respectifs des divisions euclidiennes de $x'$ et $y'$ par 5.
$$\begin{array}{|c|c|c|c|c|c|}\hline & 0 &1 &2 &3 &4 \\ \hline 0 &\textsf{A} &\textsf{B}& \textsf{C} &\textsf{D} &\textsf{E} \\ \hline 1& \textsf{F} &\textsf{G} &\textsf{H} &\textsf{I}& \textsf{J} \\ \hline 2& \textsf{K} &\textsf{L} &\textsf{M}& \textsf{N}& \textsf{O} \\ \hline 3 & \textsf{P} &\textsf{Q} &\textsf{R} &\textsf{S} &\textsf{T}\\ \hline 4 & \textsf{U} &\textsf{V} &\textsf{X} &\textsf{Y}& \textsf{Z} \\ \hline \end{array}$$ Remarque : la lettre $\textsf{W}$ est remplacée par les deux lettres accolées $\textsf{V}$.
- On utilise le tableau ci-contre pour obtenir la nouvelle lettre correspondant à la matrice colonne $\begin{pmatrix} r'\\t' \end{pmatrix}$.
- Bob et Alice choisissent la matrice $\text{M} = \begin{pmatrix} 1&2\\3&4 \end{pmatrix}$.
- Montrer que la lettre « $\textsf{T}$» du message initial est codée par la lettre « $\textsf{U}$» puis coder le message « $\textsf{TE}$» . $T$ est remplacé par la matrice $\begin{pmatrix}4\\3\end{pmatrix}$
- On pose $\text{P} = \begin{pmatrix} 3&1\\4&2 \end{pmatrix}$. Montrer que les matrices PM et $\text{I} = \begin{pmatrix} 1&0\\0&1 \end{pmatrix}$ sont congrues modulo 5. On a $PM=\begin{pmatrix} 6&10\\10&16\end{pmatrix}$
- On considère A, A' deux matrices d'ordre 2 à coefficients entiers congrues modulo 5 et $\text{Z} =\begin{pmatrix} x\\y \end{pmatrix}$, $\text{Z}' =\begin{pmatrix} x'\\y' \end{pmatrix}$ deux matrices colonnes à coefficients entiers congrues modulo 5. Montrer alors que les matrices AZ et A'Z' sont congrues modulo 5. On note $A=\begin{pmatrix} a&b\\c&d\end{pmatrix}$ et $A’=\begin{pmatrix}a’&b’\\c’&d’\end{pmatrix}$
Ainsi $\begin{pmatrix}x’\\y’\end{pmatrix}=M\begin{pmatrix}4\\3\end{pmatrix}=\begin{pmatrix}10\\24\end{pmatrix}$
Or $10\equiv 0~[5]$ et $24\equiv 4~[5]$.
Donc $\begin{pmatrix}r\\r’\end{pmatrix}=\begin{pmatrix}0\\4\end{pmatrix}$ ce qui représente la lettre $U$.
$\quad$
$E$ est remplacé par la matrice $\begin{pmatrix}4\\0\end{pmatrix}$
Ainsi $\begin{pmatrix}x’\\y’\end{pmatrix}=M\begin{pmatrix}4\\0\end{pmatrix}=\begin{pmatrix}4\\12\end{pmatrix}$
Or $4\equiv 4~[5]$ et $12\equiv 2~[5]$.
Donc $\begin{pmatrix}r\\r’\end{pmatrix}=\begin{pmatrix}4\\2\end{pmatrix}$ ce qui représente la lettre $O$.
$\quad$
Le message $TE$ est donc codé par $UO$.
$\quad$
Or $6\equiv 1~[5]$, $10\equiv 0~[5]$ et $16\equiv 1~[5]$.
Donc $PM$ et $I$ sont congrues modulo $5$.
$\quad$
Ainsi $AZ=\begin{pmatrix} ax+by\\cx+dy\end{pmatrix}$
Mais :
– si $a\equiv a’~[5]$ et $x\equiv x’~[5]$ alors $ax\equiv a’x’~[5]$
– si $e \equiv e’~[5]$ et $f\equiv f’~[5]$ alors $e+f\equiv e’+f’~[5]$.
Donc $ax+by\equiv a’x’+b’y’~[5]$ et $cx+dy\equiv c’x’+d’y’~[5]$.
Par conséquent les matrices $AZ$ et $A’Z’$ sont congrues modulo $5$.
$\quad$
Dans ce qui suit on admet que si A, A' sont deux matrices carrées d'ordre 2 à coefficients entiers congrues modulo 5 et si B, B' sont deux matrices carrées d'ordre 2 à coefficients entiers congrues modulo 5 alors les matrices produit AB et A'B' sont congrues modulo 5.
-
- On note $\text{X}= \begin{pmatrix} x_1\\x_2 \end{pmatrix}$ et $\text{Y} = \begin{pmatrix} y_1\\y_2 \end{pmatrix}$ deux matrices colonnes à coefficients entiers. Déduire des questions précédentes que si MX et Y sont congrues modulo 5 alors les matrices X et PY sont congrues modulo 5; ce qui permet de « décoder» une lettre chiffrée par la procédure utilisée par Alice et Bob avec la matrice M choisie. D’après la question précédente, les matrices $PMX$ et $PY$ sont congrues modulo $5$.
- Décoder alors la lettre « $\textsf{D}$» . La lettre $D$ est associée à la matrice $Y=\begin{pmatrix}3\\0\end{pmatrix}$
D’après la question 1.b. les matrices $PM$ et $I$ sont congrues modulo $5$.
Par conséquent, les matrices $X$ et $PY$ sont congrues modulo $5$.
$\quad$
Ainsi si on a $MX=Y$ alors, pour décoder la lettre associée à la matrice $Y$ modulo 5 il suffit de trouver la lettre associée à la matrice $PY$ modulo $5$.
$\quad$
$PY=\begin{pmatrix} 9\\12\end{pmatrix}$
qui est congrue modulo $5$ à la matrice $\begin{pmatrix} 4\\2\end{pmatrix}$.
Ainsi la lettre $D$ est décodée en $O$.
$\quad$ - On souhaite déterminer si la matrice $\text{R}=\begin{pmatrix} 1&2\\4&3 \end{pmatrix}$ peut être utilisée pour coder un message.
- On pose $\text{S} = \begin{pmatrix} 2&2\\4&4 \end{pmatrix}$. Vérifier que la matrice RS et la matrice $\begin{pmatrix} 0&0\\0&0 \end{pmatrix}$ sont congrues modulo 5. On a $RS=\begin{pmatrix} 10&10\\20&20\end{pmatrix}$ qui est bien congru modulo $5$ à la matrice $\begin{pmatrix} 0&0\\0&0\end{pmatrix}$.
- On admet qu'un message codé par la matrice R peut être décodé s‘il existe une matrice T telle que les matrices TR et I soient congrues modulo 5. Montrer que si c‘est le cas alors les matrices TRS et S sont congrues modulo 5 (par la procédure expliquée en question \textbf{1. d.} pour le codage avec la matrice M). Si $TR$ et $I$ sont congrues modulo $5$ alors, d’après la procédure fournie, les matrices $TRS$ et $IS$ sont congrues modulo $5$.
- En déduire qu‘un message codé par la matrice R ne peut être décodé. On note $Q=\begin{pmatrix} 0&0\\0&0\end{pmatrix}$
$\quad$
Cela signifie donc que $TRS$ et $S$ sont congrues modulo $5$.
$\quad$
$RS$ est $Q$ sont congrues modulo $5$
Donc $TRS$ et $TQ$ sont congrues modulo $5$.
Or $TQ=\begin{pmatrix} 0&0\\0&0\end{pmatrix}=Q$.
D’après la question précédente cela signifie donc que $I$ et $\begin{pmatrix} 0&0\\0&0\end{pmatrix}$ sont congrues modulo $5$.
Or $1$ et $0$ ne sont pas congrus modulo $5$.
Ainsi la matrice $T$ n’existe pas et un message codé par la matrice $R$ ne peut être décodé.
$\quad$
- Vues: 63221
