Baccalauréat S Pondichéry 16 avril 2013 - Correction de l'Exercice 4
Exercice 4
Dans une entreprise, on s'intéresse à la probabilité\index{probabilité} qu'un salarié soit absent durant une période d'épidémie de grippe.
- Un salarié malade est absent
- La première semaine de travail, le salarié n'est pas malade.
- Si la semaine $n$ le salarié n'est pas malade, il tombe malade la semaine $n + 1$ avec une probabilité égale à $0,04$.
- Si la semaine $n$ le salarié est malade, il reste malade la semaine $n + 1$ avec une probabilité égale à $0,24$.
On désigne, pour tout entier naturel $n$ supérieur ou égal à 1, par $E_{n}$ l'évènement « le salarié est absent pour cause de maladie la $n$-ième semaine » .
On note $p_{n}$ la probabilité de l'évènement $E_{n}$. On a ainsi : $p_{1} = 0$ et, pour tout entier naturel $n$ supérieur ou égal à 1 : $0 \leqslant p_{n} < 1$.
-
- Déterminer la valeur de $p_{3}$ à l'aide d'un arbre de probabilité.
- Sachant que le salarié a été absent pour cause de maladie la troisième semaine, déterminer la probabilité qu'il ait été aussi absent pour cause de maladie la deuxième semaine. On veut calculer la probabilité conditionnelle $p_{E_3}(E_2)=\dfrac{p(E_2\cap E_3)}{p(E_3)}=\dfrac{0,04\times 0,24}{ 0,048}=0,2$
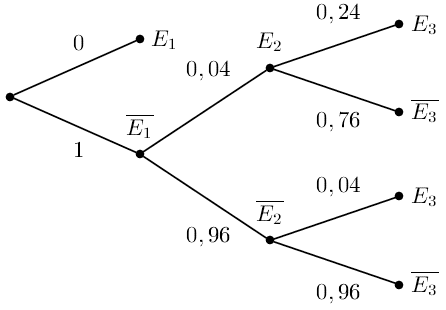 Calculons la probabilité de l'événement $E_3$.
Calculons la probabilité de l'événement $E_3$.
$E_3=\left (E_2\cap E_3 \right )\cup \left (\overline{E_2}\cap E_3\right )$.
La formule des probabilités totales donne $p(E_3)=p\left (E_2\cap E_3 \right )+p \left (\overline{E_2}\cap E_3\right )=p(E_2)\times p_{E_2}(E_3)+p(\overline{E_2})\times p_{\overline{E_2}}(E_3)$
soit $p(E_3)= 0,04\times 0,24+ 0,96\times 0,04=0,048$$p_{E_3}(E_2)= 0,2$ -
- Recopier sur la copie et compléter l'arbre de probabilité donné ci-dessous
- Montrer que, pour tout entier naturel $n$ supérieur ou égal à 1, $p_{n+ 1} = 0,2p_{n} + 0,04$. Calculons la probabilité de l'événement $E_{n+1}$.
- Montrer que la suite $\left(u_{n}\right)$ définie pour tout entier naturel $n$ supérieur ou égal à 1 par $u_{n} = p_{n} - 0,05$ est une suite géométrique dont on donnera le premier terme et la raison $r$. En déduire l'expression de $u_{n}$ puis de $p_{n}$ en fonction de $n$ et $r$. $$u_{n+1} = p_{n+1} - 0,05 = 0,2p_n + 0,04 - 0,05 = 0,2p_n - 0,01 = 0,2(p_n-0,05) = 0,2u_n$$ $u_1=−0,05$ Donc $(u_n)$ est une suite géométrique de raison 0,2 et de premier terme -0,05. Par conséquent : $$u_n=-0,05 \times 0,2^{n-1} \qquad \text{et} \qquad p_n = 0,05 – 0,05 \times 0,2^{n-1}$$
- En déduire la limite de la suite $\left(p_{n}\right)$. $\lim\limits_{n \rightarrow + \infty} 0,2^n = 0$ car $-1 < 0,2 < 1$ Donc $\lim\limits_{n \rightarrow + \infty}p_n = 0,05$
- On admet dans cette question que la suite $\left(p_{n}\right)$ est croissante. On considère l'algorithme suivant :
$$ \begin{array}{|c|c|}\hline\text{ Variables} & K \text{et} J \text{sont des entiers naturels,} P \text{est un nombre réel}\\ \text{Initialisation} & P \text{prend la valeur} 0\\ &J \text{prend la valeur} 1\\ \text{Entrée}&\text{ Saisir la valeur de } K\\ \text{Traitement} &\text{Tant que} P < 0,05 - 10^{- \text{K}}\\ &\quad P \text{prend la valeur} 0,2 \times \text{P} + 0,04\\ &\quad J \text{prend la valeur} J + 1\\ &\text{Fin tant que }\\ \text{Sortie} &\text{Afficher } J \\ \hline \end{array} $$
À quoi correspond l'affichage final J ? L'affichage final fournit le premier rang $N$ tel que $\left |p_N-0,05\right |\leq 10^{-\text{K}}$, où K est un entier choisi par l'utilisateur.
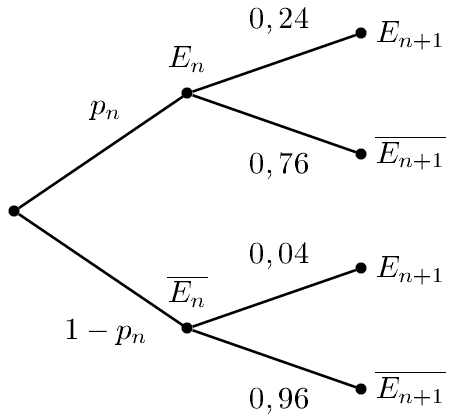
$E_{n+1}=\left (E_n\cap E_{n+1} \right )\cup \left (\overline{E_n}\cap E_{n+1}\right )$.
La formule des probabilités totales donne $p_{n+1}=p(E_{n+1})=p\left (E_n\cap E_{n+1} \right )+p \left (\overline{E_n}\cap E_{n+1}\right )=p(E_n)\times p_{E_{n+1}}(E_n)+p(\overline{E_n})\times p_{\overline{E_{n+1}}}(E_n)$
soit $p_{n+1}=p(E_{n+1})= p_n\times 0,24+ \left (1-p_n\right )\times 0,04=0,2p_n+0,04$$p_{n+1}=0,2p_n+0,04$
En effet comme $p_n=0,05-0,02\times0,2^{n-1}$, on a pour tout $n; p_n < 0,05$ et comme l'algorithme calcule en autre les termes successifs de $\left (p_n\right )$, à partir de la relation de récurrence $p_{n+1}=0,2p_n+0,04$, traduit en P prend la valeur $0,2 \times \text{P} + 0,04$
P $\geq 0,05 - 10^{- \text{K}}$ s'écrit $p_n\geq 0,05 - 10^{- \text{K}}$
On a ainsi $0,05 - 10^{- \text{K}}\leq p_n< 0,05 $ soit $- 10^{- \text{K}}\leq p_n- 0,05 < 0$
ce qui s'écrit $\left |p_N-0,05\right |\leq 10^{-\text{K}}$.Pourquoi est-on sûr que cet algorithme s'arrête ?
Comme on sait que la suite $\left (p_n\right )$ converge vers 0,05,tout intervalle ouvert $I$ centré en $0,05$ contient tous les termes de la suite à partir d'un certain rang.En particulier $I=]0,05- 10^{- \text{K}};0,05+ 10^{- \text{K}}[$ contient tous les termes de la suite à partir d'un certain rang $N$,
alors pour $n\geq N$ on a $\left |p_N-0,05\right |\leq 10^{-\text{K}}$
Cette entreprise emploie 220 salariés. Pour la suite on admet que la probabilité\index{probabilité} pour qu'un salarié soit malade une semaine donnée durant cette période d'épidémie est égale à $p = 0,05$. On suppose que l'état de santé d'un salarié ne dépend pas de l'état de santé de ses collègues. On désigne par $X$ la variable aléatoire qui donne le nombre de salariés malades une semaine donnée.
- Justifier que la variable aléatoire $X$ suit une loi binomiale dont on donnera les paramètres.
Calculer l'espérance mathématique $\mu$ et l'écart type $\sigma$ de la variable aléatoire $X$. On est en présence d'un schéma de Bernoulli: - On admet que l'on peut approcher la loi de la variable aléatoire $\dfrac{X - \mu}{\sigma}$ par la loi normale centrée réduite c'est-à-dire de paramètres $0$ et $1$.
On note $Z$ une variable aléatoire suivant la loi normale centrée réduite.
Le tableau suivant donne les probabilités de l'évènement $Z < x$ pour quelques valeurs du nombre réel $x$.
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline x & -1,55 &-1,24 &-0,93 &- 0,62 &- 0,31 &0,00 &0,31 &0,62 &0,93 &1,24 &1,55\\ \hline P(Z < x) & 0,061 &0,108 &0,177 &0,268 &0,379 &0,500 &0,621 &0,732 &0,823 &0,892 &0,939\\ \hline \end{array}$$
Calculer, au moyen de l'approximation proposée en question b., une valeur approchée à $10^{-2}$ près de la probabilité de l'évènement : « le nombre de salariés absents dans l'entreprise au cours d'une semaine donnée est supérieur ou égal à 7 et inférieur ou égal à 15 » . On veut calculer la probabilité de l'événement $7\leq X\leq 15$ qui s'écrit de façon équivalente :
Succès : « le salarié est malade une semaine donnée » avec la probabilité $p=0,05 $
Echec : « le salarié n' est pas malade une semaine donnée » avec la probabilité $q=1-p=0,95$
On répète 220 fois cette expérience de façon indépendante et on considère la variable aléatoire $X$ qui comptabilise le nombre de succès .
$X$ suit la loi binomiale $\mathcal{B}\left (220;0,02\right )$ de paramètre $n=220$ et $p=0,02$
Calculer l'espérance mathématique $\mu$ et l'écart type $\sigma$ de la variable aléatoire $X$.
$\mu =np=220\times 0,05= 11$ et $\sigma=\sqrt{npq}=\sqrt{11\times 0,95}\approx 3,23$
$$7-11\leq X -11\leq 15 -11$$
$$-4\leq X -11\leq4$$ $$-\dfrac{4}{\sigma}\leq \dfrac{X -11}{\sigma} \leq\dfrac{4}{\sigma} $$
$$-\dfrac{4}{\sigma}\leq Z \leq\dfrac{4}{\sigma} $$
Comme $\dfrac{X -11}{\sigma}$ approche la loi normale centrée réduite $Z$, on a $p\left(7\leq X\leq 15\right )\approx p\left ( -\dfrac{ 4}{\sigma}\leq Z \leq\dfrac{ 4}{\sigma}\right )$
Or $p\left ( -\dfrac{ 4}{\sigma}\leq Z \leq\dfrac{ 4}{\sigma}\right )=2\Pi\left( \dfrac{ 4}{\sigma} \right )-1 $
comme $t =\dfrac{4}{\sigma}\approx 1,24$
$$p\left(7\leq X\leq 15\right )\approx 2\Pi\left( 1,24 \right )-1 \approx 2\times 0,982-1$$
Remarque : on peut bien sûr faire le calcul avec une calculatrice
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
Enfin le calcul direct à la calculatrice !
2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$
2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$
-
$binomFR\text{é}p(220,0.05,15)-binomFR\text{é}p(220,0.05,6)\approx 0.839$
Ceci calcule la probabilité $P(X\leq 15)-P(X\leq 6)=P(7\leq X \leq 15)$ dans le cas où $X$ suit la loi binomiale $\mathcal{B}(220,0.05)$
Ceci retourne 0,839.
On peut remarquer le manque de qualité de l'approximation !
On peut améliorer cette approximation en prenant en compte la correction de continuité ...
Cette notion est hors programme mais il s'agit ici de prendre conscience du problème.A cet effet on remplace le calcul de $p(X=x)$ par $p\left (x-\frac{1}{2}\leq X\leq x+\frac{1}{2}\right )$
Par exemple $p(X=8)$ par $p\left (7,5\leq X\leq 8,5\right )$
Ici $p(7\leq X\leq 15)$ peut être remplacé par $p\left (6,5\leq X\leq 15,5\right )$ $$p\left (-\dfrac{4,5}{\sigma}\leq Z \leq\dfrac{4,5}{\sigma} \right )=2\Pi\left( \dfrac{ 4,5}{\sigma} \right )-1 $$ On obtient alors 0,836 à la calculatrice !
- Vues: 47200
