Baccalauréat S Pondichéry 4 mai 2018 - Correction Exercice 1

Page 2 sur 10: Correction Exercice 1

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

 

Les parties A et B peuvent être traitées de façon indépendante.
Dans une usine, un four cuit des céramiques à la température de 1000 ° C. À la fin de la cuisson, il est éteint et il refroidit.
On s'intéresse à la phase de refroidissement du four, qui débute dès l'instant où il est éteint.
La température du four est exprimée en degré Celsius ( °C).
La porte du four peut être ouverte sans risque pour les céramiques dès que sa température est inférieure à $70$ °C. Sinon les céramiques peuvent se fissurer, voire se casser.

Partie A

Pour un nombre entier naturel $n$, on note $T_n$ la température en degré Celsius du four au bout de $n$ heures écoulées à partir de l'instant où il a été éteint. On a donc $T_0 = 1000 $. La température $T_n$ est calculée par l'algorithme suivant : $$ \begin{array}{|cc|}\hline T \gets 1000 \\ \text{ Pour } i \text{ allant de 1 à } n \\ \hspace{1cm} T \gets 0,82 \times T + 3,6 \\ \text{Fin Pour }\\\hline \end{array}$$

1. Déterminer la température du four, arrondie à l'unité, au bout de $4$ heures de refroidissement.
La variable $T$ prend successivement les valeurs suivantes (arrondies à l’unité) :
$1000 \to 824 \to 679 \to 560 \to 463$
Au bout de $4$ heures de refroidissement la température du four est d’environ $463$ degré Celcius.

2. Démontrer que, pour tout nombre entier naturel $n$, on a : $T_n = 980 \times 0,82^n + 20$.
La suite $\left(T_n\right)$ est définie par $T_0=1~000$ et $T_{n+1}=0,82T_n+3,6$ pour tout entier naturel $n$.
Montrons par récurrence que $T_n=980\times 0,82^n+20$.
Initialisation : Si $n=0$ alors $980\times 0,82^0+20=980+20=1~000=T_0$.
La propriété est vraie au rang $0$
$\quad$
Hérédité :Soit $k\geq 0$. Supposons la propriété vraie au rang $k$ : $T_n=980\times 0,82^k+20$.
Montrons qu’elle est également vraie au rang $k+1$, c’est-à-dire que $T_{k+1}=980\times 0,82^{k+1}+20$.
$\begin{align*} T_{k+1}&=0,82T_k+3,6 \\
&=0,82\left(980\times 0,82^k+20\right)+3,6 \\
&=980\times 0,82^{k+1}+16,4+3,6 \\
&=980\times 0,82^{k+1}+20
\end{align*}$
La propriété est donc vraie au rang $k+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ on a $T_n=980\times 0,82^n+20$.

3. Au bout de combien d'heures le four peut-il être ouvert sans risque pour les céramiques ?
On veut déterminer la valeur du plus petit entier naturel $n$ tel que :
$\begin{align*} T_n\leq 70 &\iff 980\times 0,82^n+20 \leq 70 \\
&\iff 980\times 0,82^n \leq 50 \\
&\iff 0,82^n \leq \dfrac{5}{98} \\
&\iff n\ln (0,82) \leq \ln \left(\dfrac{5}{98}\right) \\
&\iff n \geq \dfrac{\ln \left(\dfrac{5}{98}\right)}{\ln (0,82)}
\end{align*}$
Or $\dfrac{\ln \left(\dfrac{5}{98}\right)}{\ln (0,82)}\approx 14,99$.
Donc le four peut être ouvert sans risque pour les céramiques au bout de $15$ heures.

 

Partie B

Dans cette partie, on note $t$ le temps (en heure) écoulé depuis l'instant où le four a été éteint. La température du four (en degré Celsius) à l'instant $t$ est donnée par la fonction $f$ définie, pour tout nombre réel $t$ positif, par : $$f(t) = a\text{e}^{- \frac{t}{5}} + b, $$ où $a$ et $b$ sont deux nombres réels. On admet que $f$ vérifie la relation suivante : $f'(t) + \dfrac{1}{5}f(t) = 4$.

1. Déterminer les valeurs de $a$ et $b$ sachant qu'initialement, la température du four est de $ 1000 $ ° C, c'est-à-dire que $f(0) = 1000 $.
On a $f(0)=1~000$ et $f(0)=a+b$ donc $a+b=1~000 \quad (1)$
On sait de plus que $f'(t)+\dfrac{1}{5}f(t)=4$
Or $f'(t)=-\dfrac{a}{5}\text{e}^{-t/5}$
Donc $-\dfrac{a}{5}\text{e}^{-t/5}+\dfrac{1}{5}\left(a\text{e}^{-t/5}+b\right)=4$ pour tout réel $t$ positif.
En particulier, quand $t=0$ on a : $-\dfrac{a}{5}+\dfrac{a+b}{5}=4$
soit $-a+a+b=20 \iff b=20$
On en déduit donc, en utilisant l’équation $(1)$ que $a+20=1~000 \iff a=980$.

2. Pour la suite, on admet que, pour tout nombre réel positif $t$: $$f(t) = 980\text{e}^{- \frac{t}{5}} + 20.$$
   
   1. Déterminer la limite de $f$ lorsque $t$ tend vers $+ \infty$.
   $\lim\limits_{t \to +\infty} -\dfrac{t}{5}=-\infty$.
   $\lim\limits_{T \to -\infty} \text{e}^T=0$
   Donc $\lim\limits_{t \to +\infty} \text{e}^{-t/5}=0$
   Ainsi $\lim\limits_{t \to +\infty} f(t)=20$.
   $\quad$
   
   2. Étudier les variations de $f$ sur $[0~;~+ \infty[$. En déduire son tableau de variations complet.
   On a $f'(t)=-\dfrac{980}{5}\text{e}^{-t/5}=-196\text{e}^{-t/5}$.
   La fonction exponentielle étant strictement positive, on a donc $f'(t)<0$ pour tout réel $t$ positif.
   La fonction $f$ est donc décroissante sur $[0;+\infty[$.
   On obtient ainsi le tableau de variations suivant :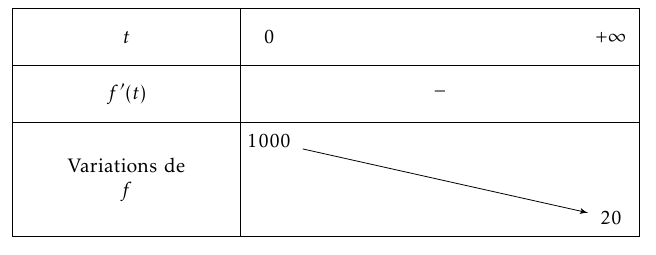
   
   
   3. Avec ce modèle, après combien de minutes le four peut-il être ouvert sans risque pour les céramiques ?
   On veut résoudre :
   $\begin{align*} f(t)\leq 70 &\iff 980\text{e}^{-t/5}+20 \leq 70 \\
   &\iff 980 \text{e}^{-t/5}\leq 50 \\
   &\iff \text{e}^{-t/5} \leq \dfrac{5}{98} \\
   &\iff -\dfrac{t}{5} \leq \ln \left( \dfrac{5}{98}\right) \\
   &\iff t \geq -5\ln \left( \dfrac{5}{98}\right)
   \end{align*}$$-5\ln \left( \dfrac{5}{98}\right) \approx 14,878$
   On peut donc ouvrir le four sans risque au bout de $893$ minutes.
   $\quad$
3. La température moyenne (en degré Celsius) du four entre deux instants $t_1$ et $t_2$ est donnée par: $\dfrac{1}{t_2 - t_1}\displaystyle\int_{t_1}^{t_2} f(t)\:\text{d}t$.
   1. À l'aide de la représentation graphique de $f$ ci-dessous, donner une estimation de la température moyenne $\theta$ du four sur les $15$ premières heures de refroidissement. Expliquer votre démarche.
      
      
   
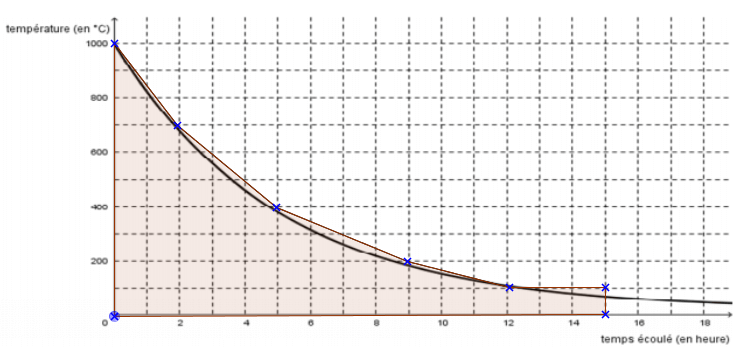
   On a donc l’aire de $4$ trapèzes et celle d’un rectangle.
   $\begin{align*} \mathscr{A}&=\dfrac{(1~000+700)\times 2}{2}+\dfrac{(700+400)\times 3}{2} \\
   &+\dfrac{(400+200)\times 4}{2}+\dfrac{(200+100)\times 3}{2}+100\times 3 \\
   &=5~300
   \end{align*}$
   La fonction $f$ est continue et positive sur l’intervalle $[0;15]$. L’aire du domaine compris entre la courbe représentant la fonction $f$, l’axe des abscisses et les droites d’équation $x=0$ et $x=15$ est $\displaystyle \int_0^{15}f(t)\:\text{d}t$.
   Une approximation de $\displaystyle \int_0^{15}f(t) \:\text{d}t$ est $5~300$ u.a.
   Ainsi une valeur approchée de la température moyenne du four sur les $15$ premières heures de refroidissement est $\theta=\dfrac{5~300}{15} \approx 353$ degré Celcius.
   $\quad$
   
   2. Calculer la valeur exacte de cette température moyenne $\theta$ et en donner la valeur arrondie au degré Celsius.
On a :
$\begin{align*} \theta&=\dfrac{1}{15}\displaystyle \int_0^{15} f(t)\:\text{d}t \\
&=\dfrac{1}{15}\int_0^{15} \left(980\text{e}^{-t/5}+20\right)\:\text{d}t \\
&=\dfrac{1}{15}\left[-5\times 980\text{e}^{-t/5}+20t\right]_0^{15} \\
&=\dfrac{1}{15}\left(-4~900\text{e}^{-3}+300+4~900\right) \\
&=\dfrac{5~200-4~900\text{e}^{-3}}{15} \\
&\approx 330
\end{align*}$

4. Dans cette question, on s'intéresse à l'abaissement de température (en degré Celsius) du four au cours d'une heure, soit entre deux instants $t$ et $(t + 1)$. Cet abaissement est donné par la fonction $d$ définie, pour tout nombre réel $t$ positif, par : $d(t) = f(t) - f(t + 1)$.
   1. Vérifier que. pour tout nombre réel $t$ positif: $d(t) = 980\left(1 - \text{e}^{- \frac{1}{5}}\right)\text{e}^{- \frac{t}{5}}$.
   $\begin{align*} d(t)&=f(t)-f(t+1) \\
   &=980\text{e}^{-t/5}+20-\left(980\text{e}^{-(t+1)/5}+20\right) \\
   &=980\text{e}^{-t/5}-980\text{e}^{-(t+1)/5} \\
   &=980\text{e}^{-t/5}\left(1-\text{e}^{-1/5}\right)
   \end{align*}$
   $\quad$
   
   2. Déterminer la limite de $d(t)$ lorsque $t$ tend vers $+ \infty$. Quelle interprétation peut-on en donner ?
   On a vu que $\lim\limits_{t \to +\infty} \text{e}^{-t/5}=0$
   Donc $\lim\limits_{t \to +\infty} d(t)=0$.
   Cela signifie que l’écart de température entre deux instants séparés d’une heure devient de plus en plus proche de $0$ et donc, qu’au bout d’un certain temps, la température du four se stabilise.