Baccalauréat S Polynésie 20 juin 2018 - Correction Exercice 3

Page 6 sur 10: Correction Exercice 3

Correction de l'exercice 3 (4 points)

Commun à tous les candidats

Fonctions

On considère la fonction $f$ définie sur l'intervalle $[0~;~ +\infty[$ par $f(x) = k\text{e}^{-kx}$ où $k$ est un nombre réel strictement positif. On appelle $\mathcal{C}_f$ sa représentation graphique dans le repère orthonormé $\left(\text{O}~;~\vec{\imath},~\vec{\jmath}\right)$. On considère le point A de la courbe $\mathcal{C}_f$ d'abscisse 0 et le point B de la courbe $\mathcal{C}_f$ d'abscisse 1. Le point C a pour coordonnées $(1~;~0)$.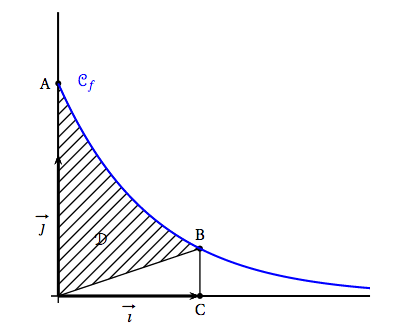

1. Déterminer une primitive de la fonction $f$ sur l'intervalle $[0~;~ +\infty[$.
Une primitive de la fonction $f$ sur l’intervalle $[0;+\infty[$ est la fonction $F$ définie par $F(x)=-\text{e}^{-kx}$.
$\quad$
2. Exprimer, en fonction de $k$, l'aire du triangle OCB et celle du domaine $\mathcal{D}$ délimité par l'axe des ordonnées, la courbe $\mathcal{C}_f$ et le segment [OB].
On a $BC=f(1)=k\text{e}^{-k}$.
L’aire du triangle $OBC$ est donc $V_1=\dfrac{1\times k\text{e}^{-k}}{2}=\dfrac{k\text{e}^{-k}}{2}$.
$\quad$
La fonction $f$ est continue et positive sur l’intervalle $[0;+\infty[$.
L’aire du domaine $\mathscr{D}$ est donc :
$\begin{align*} V_2&=\displaystyle \int_0^1 f(x)\text{d}x-V_1 \\
&=F(1)-F(0)-\dfrac{k\text{e}^{-k}}{2} \\
&=1-\text{e}^{-k}-\dfrac{k\text{e}^{-k}}{2} \\
&=1-\dfrac{(2+k)\text{e}^{-k}}{2} \\
\end{align*}$
$\quad$
3. Montrer qu'il existe une unique valeur du réel $k$ strictement positive telle que l'aire du domaine $\mathcal{D}$ vaut le double de celle du triangle OCB.
On veut résoudre l’équation
$ 1-\text{e}^{-k}-\dfrac{k\text{e}^{-k}}{2}=k\text{e}^{-k} \iff 1-\text{e}^{-k}-\dfrac{3k}{2}\text{e}^{-k} = 0 $
On considère la fonction $g$ définie sur $]0;+\infty[$ par $g(x)=1-\text{e}^{-x}-\dfrac{3x}{2}\text{e}^{-x}$
La fonction $g$ est continue sur $]0;+\infty[$ comme somme et produit de fonctions continues sur cet intervalle.
Elle est également dérivable sur cet intervalle comme somme et produit de fonctions dérivables sur $]0;+\infty[$.
Pour tout réel $x>0$ on a :
$\begin{align*} g'(x)&=\text{e}^{-x}-\dfrac{3}{2}\text{e}^{-x}+\dfrac{3x}{2}\text{e}^{-x} \\
&=\dfrac{-1+3x}{2}\text{e}^{-x}
\end{align*}$
La fonction exponentielle est strictement positive sur l’intervalle $]0;+\infty[$.
Le signe de $g'(x)$ ne dépend donc que de celui de $-1+3x$.
Or $-1+3x=0 \iff x=\dfrac{1}{3}$
Et $-1+3x>0 \iff x>\dfrac{1}{3}$
On obtient le tableau de variation suivant :

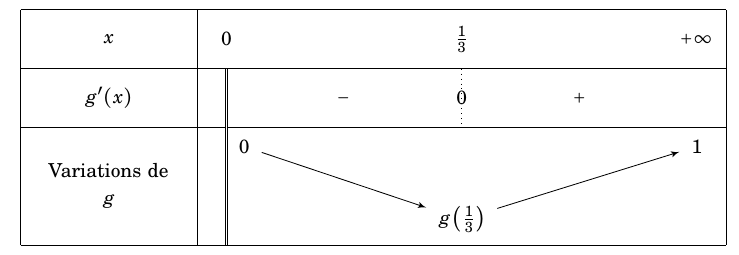
$1-\text{e}^{-0}-\dfrac{3\times 0}{2}\text{e}^{-0}=0$ donc $\lim\limits_{x \to 0^+} g(x)=0$.
$\lim\limits_{x \to +\infty} -x=-\infty$ et $\lim\limits_{X \to -\infty} \text{e}^X=0$.
Donc  $\lim\limits_{x \to +\infty} \text{e}^{-x}=0$
$\lim\limits_{x \to +\infty} -x=-\infty$ et $\lim\limits_{X \to -\infty} X\text{e}^X=0$.
Donc  $\lim\limits_{x \to +\infty} -x\text{e}^{-x}=0$
Par conséquent $\lim\limits_{x\to +\infty} g(x)=1$.
$g\left(\dfrac{1}{3}\right) \approx -0,07$.
$\quad$
Sur l’intervalle $\left]0;\dfrac{1}{3}\right]$ on a $g(x)<0$.
L’équation $g(x)=0$ ne possède donc pas de solution sur cet intervalle.
Sur l’intervalle $\left]\dfrac{1}{3};+\infty\right[$, la fonction $g$ est continue et strictement croissante.
$g\left(\dfrac{1}{3}\right)<0$ et $\lim\limits_{x\to +\infty} g(x)=1>0$
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation $g(x)=0$ possède une unique solution sur l’intervalle $\left]\dfrac{1}{3};+\infty\right[$.
L’équation $g(x)=0$ possède donc une unique solution sur l’intervalle $]0;+\infty$.
Par conséquent il existe une unique valeur du réel $k$ strictement positive telle que l’aire du domaine $\mathscr{D}$ vaut le double de celle du triangle $OCB$.
$\quad$