Baccalauréat S Métropole 22 juin 2018 - Correction Exercice 4
Page 8 sur 10
Correction de l'exercice 4 5 points
Le plan complexe est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. On pose $z_0 = 8$ et, pour tout entier naturel $n$ : \[z_{n+1} = \dfrac{3 - \text{i}\sqrt{3}}{4}z_n.\] On note $A_n$ le point du plan d'affixe $z_n$.
-
- Vérifier que : \[\dfrac{3 - \text{i}\sqrt{3}}{4} = \dfrac{\sqrt{3}}{2}\text{e}^{- \text{i}\frac{\pi}{6}}.\] $\begin{align*} \dfrac{\sqrt{3}}{2}\text{e}^{-\text{i}\pi/6}&=\dfrac{\sqrt{3}}{2}\left(\cos\left(-\dfrac{\pi}{6}\right)+\text{i} \sin \left(-\dfrac{\pi}{6}\right)\right) \\
- En déduire l'écriture de chacun des nombres complexes $z_1$, $z_2$ et $z_3$ sous forme exponentielle et vérifier que $z_3$ est un imaginaire pur dont on précisera la partie imaginaire. On a donc :
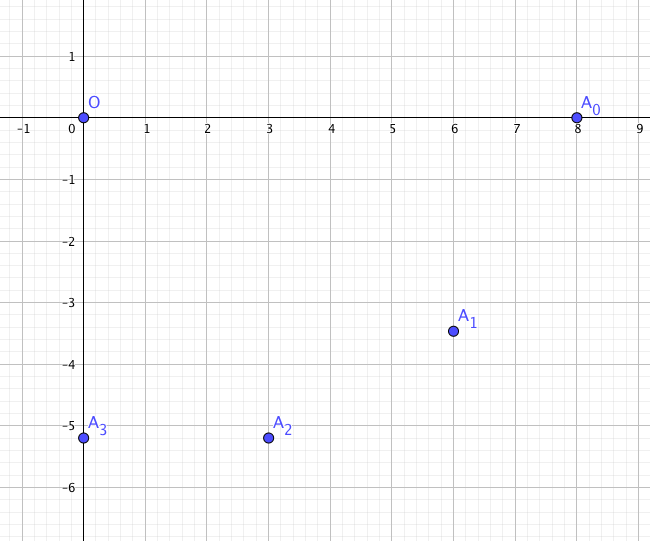
- Représenter graphiquement les points $A_0$ , $A_1$ , $A_2$ et $A_3$ ; on prendra pour unité le centimètre.
&=\dfrac{\sqrt{3}}{2}\left(\dfrac{\sqrt{3}}{2}-\dfrac{\text{i}}{2}\right) \\
&=\dfrac{3}{4}-\dfrac{\text{i}\sqrt{3}}{4} \\
&=\dfrac{3-\text{i}\sqrt{3}}{4}
\end{align*}$
$\quad$
$z_1=\dfrac{3-\text{i}\sqrt{3}}{4} \times 8 =8 \times \dfrac{\sqrt{3}}{2}\text{e}^{-\text{i}\pi/6} = 4\sqrt{3}\text{e}^{-\text{i}\pi/6}$
$z_2=\dfrac{3-\text{i}\sqrt{3}}{4} \times 4\sqrt{3}\text{e}^{-\text{i}\pi/6} = 4\sqrt{3}\text{e}^{-\text{i}\pi/6} \times \dfrac{\sqrt{3}}{2}\text{e}^{-\text{i}\pi/6} = 6\text{e}^{-\text{i} \pi/3}$
$z_3=\dfrac{3-\text{i}\sqrt{3}}{4} \times 6\text{e}^{-\text{i} \pi/3} = \dfrac{\sqrt{3}}{2}\text{e}^{-\text{i}\pi/6} \times 6\text{e}^{-\text{i} \pi/3}=3\sqrt{3}\text{e}^{-\text{i}\pi/2}$
On a donc $z_3=-3\text{i}\sqrt{3}$ est un nombre imaginaire pur dont la partie imaginaire est $-3\sqrt{3}$.
$\quad$
-
- Démontrer par récurrence que, pour tout entier naturel $n$, \[z_n = 8 \times \left(\dfrac{\sqrt{3}}{2}\right)^n \text{e}^{- \text{i}\frac{n\pi}{6}}.\] Initialisation : Si $n=0$ alors $8\times \left(\dfrac{\sqrt{3}}{2}\right)^0\text{e}{0}=8=z_0$.
- Pour tout entier naturel $n$, on pose $u_n = \left|z_n\right|$. Déterminer la nature et la limite de la suite $\left(u_n\right)$. Pour tout entier naturel $n$ on a :
La propriété est vraie au rang $0$.
$\quad$
Hérédité : Supposons vraie la propriété au rang $n$ : $z_n=8\times \left(\dfrac{\sqrt{3}}{2}\right)^n\times \text{e}^{-\text{i} n \pi/6}$.
Montrons qu’elle est vraie au rang suivant : $z_{n+1}=8\times \left(\dfrac{\sqrt{3}}{2}\right)^{n+1}\times \text{e}^{-\text{i} (n+1) \pi/6}$
$\begin{align*} z_{n+1}&= \dfrac{3-\text{i}\sqrt{3}}{4}z_n \\
&=\dfrac{\sqrt{3}}{2}\text{e}^{-\text{i} \pi/6} \times 8\times \left(\dfrac{\sqrt{3}}{2}\right)^n\times \text{e}^{-\text{i} n \pi/6}\\
&=8\times \left(\dfrac{\sqrt{3}}{2}\right)^{n+1}\times \text{e}^{-\text{i} (n+1) \pi/6}
\end{align*}$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$, on a $z_n=8\times \left(\dfrac{\sqrt{3}}{2}\right)^n\times \text{e}^{-\text{i} n \pi/6}$.
$\quad$
$u_n=\left|z_n\right|=8\times \left(\dfrac{\sqrt{3}}{2}\right)^n$.
La suite $\left(u_n\right)$ est donc géométrique de raison $\dfrac{\sqrt{3}}{2}$ et de premier terme $u_0=8$
Or $-1< \dfrac{\sqrt{3}}{2} <1$ donc $\lim\limits_{n \to +\infty} \left(\dfrac{\sqrt{3}}{2}\right)^n=0$
et $\lim\limits_{n \to +\infty} u_n=0$.
$\quad$ -
- Démontrer que, pour tout entier naturel $k$, \[\dfrac{z_{k+1} - z_{k}}{z_{k+1}} = - \dfrac{1}{\sqrt{3}}\text{i}.\] En déduire que, pour tout entier naturel $k$, on a l'égalité : $A_kA_{k+1} = \dfrac{1}{\sqrt{3}} \text{O}A_{k+1}$. Pour tout entier naturel $k$ on a :
- Pour tout entier naturel $n$, on appelle $\ell_n$ la longueur de la ligne brisée reliant dans cet ordre les points $A_0$,$\:$ $A_1$,$\:$ $A_2$, $\ldots$ , $A_n$.
On a ainsi : $\ell_n = A_0A_1 + A_1A_2 + \ldots + A_{n-1}A_n$.
Démontrer que la suite $\left(\ell_n\right)$ est convergente et calculer sa limite. Pour tout entier naturel $n$ on a :
$\begin{align*} \dfrac{z_{k+1}-z_k}{z_{k+1}} &=1-\dfrac{z_k}{z_{k+1}} \\
&=1-\dfrac{ 8\times \left(\dfrac{\sqrt{3}}{2}\right)^k\times \text{e}^{-\text{i} k \pi/6}}{8\times \left(\dfrac{\sqrt{3}}{2}\right)^{k+1}\times \text{e}^{-\text{i} (k+1) \pi/6}} \\
&=1-\dfrac{1}{\dfrac{\sqrt{3}}{2}\text{e}^{\text{i}\pi/6}} \\
&=1-\dfrac{2\text{e}^{\text{i} \pi/6}}{\sqrt{3}} \\
&=1-\dfrac{2}{\sqrt{3}}\left(\dfrac{\sqrt{3}}{2}+\dfrac{\text{i}}{2}\right) \\
&=1-1-\dfrac{1}{\sqrt{3}}\text{i} \\
&=-\dfrac{1}{\sqrt{3}}\text{i}
\end{align*}$
$\quad$
Cela signifie donc que $\left|\dfrac{z_{k+1}-z_k}{z_{k+1}}\right|=\dfrac{1}{\sqrt{3}} \iff \dfrac{A_kA_{k+1}}{OA_{k+1}}=\dfrac{1}{\sqrt{3}}$
Soit $A_kA_{k+1}=\dfrac{1}{\sqrt{3}}OA_{k+1}$.
$\quad$
$\begin{align*} \ell_n=\dfrac{1}{\sqrt{3}}OA_1+\dfrac{1}{\sqrt{3}}OA_2+\ldots +\dfrac{1}{\sqrt{3}}OA_n \\
&=\dfrac{1}{\sqrt{3}}\left(u_1+u_2+\ldots+u_n\right) \\
&=\dfrac{1}{\sqrt{3}}\times u_1\times \dfrac{1-\left(\dfrac{\sqrt{3}}{2}\right)^{n}}{1-\dfrac{\sqrt{3}}{2}} \\
&=\dfrac{4\sqrt{3}}{\sqrt{3}}\times \dfrac{1-\left(\dfrac{\sqrt{3}}{2}\right)^{n}}{1-\dfrac{\sqrt{3}}{2}} \\
&=4\times \dfrac{1-\left(\dfrac{\sqrt{3}}{2}\right)^{n}}{1-\dfrac{\sqrt{3}}{2}}
\end{align*}$
Or $\lim\limits_{n \to +\infty} \left(\dfrac{\sqrt{3}}{2}\right)^n=0$
Donc $\lim\limits_{n \to \infty} \ell_n= \dfrac{4}{1-\dfrac{\sqrt{3}}{2}}= \dfrac{8}{2-\sqrt{3}} \approx 29,86 $
La suite $\left(\ell_n\right)$ est bien convergente.
$\quad$
- Vues: 54311
