Baccalauréat S Métropole--La Réunion 13 septembre 2018 - Correction Exercice 3
Correction de l'exercice 3 (5 points)
Le candidat indiquera sur la copie le numéro de la question suivi de la réponse choisie.
Aucune justification n'est demandée.
Il est attribué $1,5$ point par réponse correcte.
Aucun point n'est enlevé en l'absence de réponse ou en cas de réponse incorrecte.
- Question 1
Dans l'espace rapporté à un repère orthonormé $\left(\text{O}, \vec{i}, \vec{j}, \vec{k}\right)$ , on considère la droite $(D)$ de représentation paramétrique $\left\{\begin{array}{l c l} x &=&2+ \phantom{3}t\\ y &=& 1 - 3t\\ z &=& \phantom{2 +} 2t \end{array}\right. (t \in \mathbb{R})$, et le plan $(P)$ d'équation cartésienne $x + y + z - 3 = 0$.
On peut affirmer que :
- Réponse A : la droite $(D)$ et le plan $(P)$ sont strictement parallèles.
- Réponse B : la droite $(D)$ est incluse dans le plan $(P)$.
- Réponse C : la droite $(D)$ et le plan $(P)$ se coupent au point de coordonnées $(4 ; -5 ; 4)$.
- Réponse D : la droite $(D)$ et le plan $(P)$ sont orthogonaux.
- Question 2
Dans le rayon informatique d'une grande surface, un seul vendeur est présent et les clients sont nombreux. On admet que la variable aléatoire $T$, qui, à chaque client, associe le temps d'attente en minutes pour que le vendeur soit disponible, suit une loi exponentielle de paramètre $\lambda$. Le temps d'attente moyen est de $20$ minutes. Sachant qu'un client a déjà attendu $20$ minutes, la probabilité que son attente totale dépasse une demi-heure est:
- Réponse A : $\text{e}^{-\frac{1}{2}}$
- Réponse B : $\text{e}^{-\frac{3}{2}}$
- Réponse C : $1- \text{e}^{-\frac{1}{2}}$
- Réponse D : $1 - \text{e}^{-10\lambda}$
- Question 3
Une usine fabrique des balles de tennis en grande quantité. Pour être conforme au règlement des compétitions internationales, le diamètre d'une balle doit être compris entre $63,5$ mm et $66,7$ mm. On note $D$ la variable aléatoire qui, à chaque balle produite, associe son diamètre mesuré en millimètres. On admet que $D$ suit une loi normale de moyenne $65,1$ et d'écart type $\sigma$. On appelle $P$ la probabilité qu'une balle choisie au hasard dans la production totale soit conforme. L'usine décide de régler les machines de sorte que $P$ soit égale à $0,99$. La valeur de $\sigma$, arrondie au centième, permettant d'atteindre cet objectif est:
- Réponse A : 0,69
- Réponse B : 2,58
- Réponse C : 0,62
- Réponse D : 0,80
- Question 4
La courbe ci-dessous est la représentation graphique, dans un repère orthonormé, de la fonction $f$ définie par : \[f(x) = \dfrac{4x}{x^2 + 1}.\]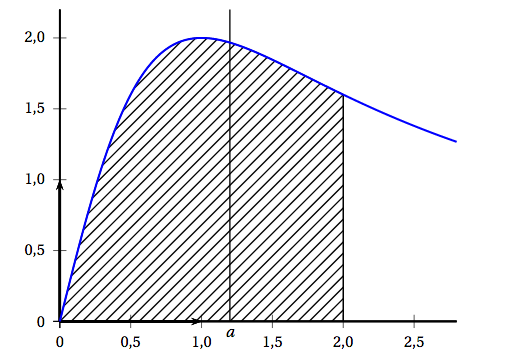
- La valeur exacte du réel positif $a$ tel que la droite d'équation $x = a$ partage le domaine hachuré en deux domaines d'aires égales est :
- Réponse A : $\sqrt{\sqrt{\dfrac{3}{2}}}$
- Réponse B : $\sqrt{\sqrt{5} - 1}$
- Réponse C : $\ln 5 - 0,5$
- Réponse D : $\dfrac{10}{9}$
On a la représentation paramétrique de la droite $(D)$ : $\begin{cases} x=2+t\\y=1-3t\\z=2t\end{cases} \quad t\in \mathbb{R}$.
On a donc :
$x+y+z-3=2+t+1-3t+2t-3=0$.
La représentation paramétrique de la droite $(D)$ vérifie donc l’équation cartésienne du plan $(P)$.
La droite $(D)$ est incluse dans le plan $(P)$.
Réponse B
$\quad$
Le temps d’attente moyen est de $20$ minutes. Par conséquent $\dfrac{1}{\lambda} = 20 \iff \lambda =\dfrac{1}{20}=0,05$.
On veut calculer :
$P_{(T>20)}(T>30)=P_{(T>20)}(T>20+10)=P(T>10)$ puisque la loi exponentielle est une loi à durée de vie sans vieillissement.
Or $P(T>10)=\text{e}{-10\lambda}=\text{e}{-0,5}$.
Réponse A
$\quad$
La variable aléatoire $X=\dfrac{D-\mu}{\sigma}=\dfrac{D-65,1}{\sigma}$ suit la loi normale centrée réduite.
On veut que :
$\begin{align*} P(63,5 < D <66,7)=0,99&\iff P(-1,6<D-65,1<1,6)=0,99 \\
&\iff P\left(\dfrac{-1,6}{\sigma}<\dfrac{D-65,1}{\sigma}<\dfrac{1,6}{\sigma}\right)=0,99 \\
&\iff P\left(\dfrac{-1,6}{\sigma}<X<\dfrac{1,6}{\sigma}\right)=0,99 \\
&\iff 2P\left(X<\dfrac{1,6}{\sigma}\right)-1=0,99 \\
&\iff 2P\left(X<\dfrac{1,6}{\sigma}\right)=1,99 \\
&\iff P\left(X<\dfrac{1,6}{\sigma}\right)=0,995 \end{align*}$
D’après la calculatrice on a $\dfrac{1,6}{\sigma} \approx 2576$ donc $\sigma \approx 0,621$.
Réponse C
$\quad$
Remarque : Il faut bien penser à vérifier que la valeur trouvée permet d’avoir la probabilité demandée
Remarque 2 : Comme il s’agit d’un QCM, on peut également tester à la calculatrice toutes les valeurs proposées.
$\quad$
On a $f(x)=\dfrac{4x}{x^2+1}=\dfrac{2\times 2x}{x^2+1}$. Ainsi une primitive de la fonction $f$ est la fonction $F$ définie sur $\mathbb{R}$ par $F(x)=2\ln\left(x^2+1\right)$.
La fonction $f$ est continue et positive sur l’intervalle $[0;+\infty[$.
On veut donc que :
$\begin{align*} \displaystyle \int_0^a f(x)\:\text{d}x=\dfrac{1}{2}\int_0^2 f(x)\:\text{d}x &\iff F(a)-F(0)=\dfrac{1}{2}\left(F(2)-F(0)\right) \\
&\iff 2\ln\left(a^2+1\right)=\dfrac{2\ln(5)}{2} \\
&\iff \ln\left(a^2+1\right)=\dfrac{\ln(5)}{2} \\
&\iff \ln \left(a^2+1\right)=\ln\left(\sqrt{5}\right) \\
&\iff a^2+1=\sqrt{5} \\
&\iff a^2=\sqrt{5}-1 \\
&\iff a=\sqrt{\sqrt{5}-1} \quad \text{car } a>0\end{align*}$.
Réponse B
$\quad$
Remarque : ici encore, il faut penser à vérifier la valeur trouvée à l’aide de la calculatrice .
Remarque 2 : Il était possible de tester les valeurs proposées et de ne retenir que celle qui permettait d’obtenir le résultat escompté.
$\quad$
- Vues: 35070
