Baccalauréat S Métropole--La Réunion 13 septembre 2018 - Correction Exercice 2
Page 4 sur 10
Correction de l'exercice 2 (5 points)
Le plan complexe est rapporté à un repère orthonormé direct $\left(\text{O}, \vec{u}, \vec{v}\right)$. On prendra pour unité graphique le centimètre.
- Résoudre dans $\mathbb{C}$ l'équation $\left(z^2 - 2z + 4\right)\left(z^2 + 4\right) = 0$. Un produit de facteur est nul si, et seulement si, un de ses facteurs au moins est nul.
- On considère les points A et B d'affixes respectives $z_{\text{A}} = 1 + \text{i}\sqrt{3}$ et $z_{\text{B}} = 2\text{i}$.
- Écrire $z_{\text{A}}$ et $z_{\text{B}}$ sous forme exponentielle et justifier que les points A et B sont sur un cercle de centre O dont on précisera le rayon. $\left|1+\text{i} \sqrt{3}\right|=\sqrt{1+3}=2$.
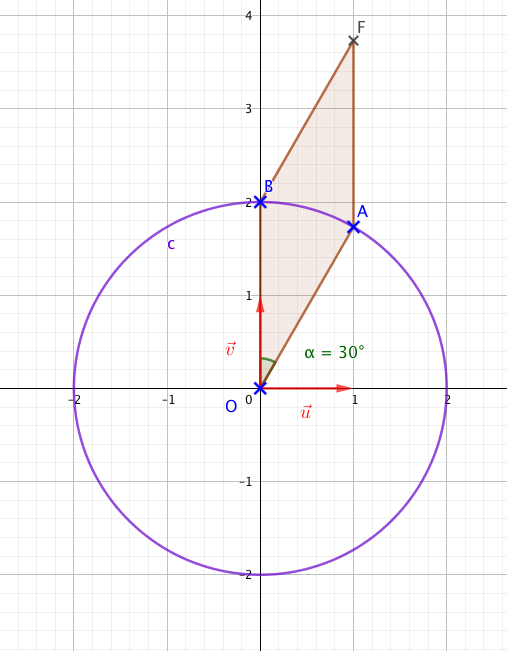
- Faire une figure et placer les points A et B.
- Déterminer une mesure de l'angle $\left(\vec{\text{OA}}, \vec{\text{OB}}\right)$. On a :
Donc $z_A=2\left(\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\text{i}\right)=2\text{e}^{\text{i} \pi/3}$
$z_B=2\text{i}=2\text{e}^{\text{i} \pi/2}$.
$\quad$
On a $\left|z_A\right|=\left|z_B\right|=2$.
Les points $A$ et $B$ appartiennent donc au cercle de centre $0$ et de rayon $2$.
$\quad$
$\begin{align*} \dfrac{z_B-z_O}{z_A-z_O}&=\dfrac{2\text{e}^{\text{i}\pi/2}}{2\text{e}^{\text{i} \pi/3}} \\
&=\text{e}^{\text{i}\left(\pi/2-\pi_3\right)} \\
&=\text{e}^{\text{i} \pi/6}
\end{align*}$
Une mesure de l’angle $\left(\vec{OA};\vec{OB}\right)$ est $\dfrac{\pi}{6}$ rad.
$\quad$ - On note F le point d'affixe $z_{\text{F}} = z_{\text{A}} + z_{\text{B}}$.
- Placer le point F sur la figure précédente. Montrer que OAFB est un losange.
- En déduire une mesure de l'angle $\left(\vec{\text{OA}}, \vec{\text{OF}}\right)$ puis de l'angle $\left(\vec{u}, \vec{\text{OF}}\right)$. Voir figure
- Calculer le module de $z_{\text{F}}$ et en déduire l'écriture de $z_{\text{F}}$ sous forme trigonométrique. Par conséquent $\left(\vec{OA};\vec{OF}\right)=\dfrac{1}{2}\left(\vec{OA};\vec{OF}\right)$.
- En déduire la valeur exacte de : \[\cos \left(\dfrac{5\pi}{12}\right).\] $z_F=z_A+z_B=1+\text{i}\left(\sqrt{3}+2\right)$.
$\quad$
L’affixe de $\vec{OA}$ est $z_{\vec{OA}}=z_A$.
L’affixe de $\vec{BF}$ est $z_{\vec{BF}}=z_F-z_B=z_A+z_B-z_B=z_A$.
Par conséquent $\vec{OA}=\vec{BF}$ et le quadrilatère $OAFB$ est un parallélogramme.
De plus $OA=OB$ puisque $A$ et $B$ appartiennent au cercle de centre $O$ et de rayon $2$.
$OAFB$ est donc un losange.
$\quad$
Une mesure de l’angle $\left(\vec{OA};\vec{OF}\right)$ est $\dfrac{\pi}{12}$ rad.
$\quad$
On a $\left(\vec{u};\vec{OF}\right)=\left(\vec{u};\vec{OA}\right)+\left(\vec{OA};\vec{OF}\right)$
Une mesure de l’angle $\left(\vec{u};\vec{OF}\right)$ est donc $\dfrac{\pi}{3}+\dfrac{\pi}{12}=\dfrac{5}{12}$ rad.
$\quad$
Donc
$\begin{align*} \left|z_F\right|&=\sqrt{1^2+\left(\sqrt{3}+2\right)^2}\\
&=\sqrt{1+3+4+4\sqrt{3}} \\
&=\sqrt{8+4\sqrt{3}}
\end{align*}$
Par conséquent $z_F=\sqrt{8+4\sqrt{3}}\text{e}^{5\text{i}\pi/12}$.
$\quad$
On a donc : $\sqrt{8+4\sqrt{3}}\text{e}^{5\text{i}\pi/12}=1+\text{i}\left(\sqrt{3}+2\right)$
$\iff \sqrt{8+4\sqrt{3}}\left(\cos\left(\dfrac{5\text{i}\pi}{12}\right)+\text{i} \sin\left(\dfrac{5\text{i}\pi}{12}\right)\right)=1+\text{i}\left(\sqrt{3}+2\right)$
Donc $\cos\left(\dfrac{5 \pi}{12}\right)=\dfrac{1}{\sqrt{8+4\sqrt{3}}}$.
$\quad$ - Deux modèles de calculatrice de marques différentes donnent pour l'une: \[\cos \left(\dfrac{5\pi}{12}\right) = \dfrac{\sqrt{2 - \sqrt{3}}}{2}\] et pour l'autre : \[\cos \left(\dfrac{5\pi}{12}\right) = \dfrac{\sqrt{6} - \sqrt{2}}{4}.\] Ces résultats sont-ils contradictoires ? Justifier la réponse. Comparons les carrés de ces deux nombres.
Donc $\left(z^2-2z+4\right)\left(z^2+4\right)=0 \iff z^2-2z+4=0\quad \text{ou} \quad z^2+4=0$
On s’intéresse à l’équation $z^2-2z+4=0$
$\Delta = (-2)^2-4\times 4=4-16=-12<0$
L’équation possède donc $2$ racines complexes :
$z_1=\dfrac{2-\text{i}\sqrt{12}}{2}=1-\text{i}\sqrt{3}$ et $z_2=\overline{z_1}=1+\text{i}\sqrt{3}$.
$\quad$
Ensuite $z^2+4=0 \iff z^2=-4 \iff z=-2\text{i} \text{ ou } z=2\text{i}$.
$\quad$
Les solutions de $\left(z^2-2z+4\right)\left(z^2+4\right)=0$ sont donc : $-2\text{i}$ ; $2\text{i}$ ; $1-\text{i} \sqrt{3}$ et $1+\text{i} \sqrt{3}$.
$\quad$
$\left(\dfrac{\sqrt{2-\sqrt{3}}}{2}\right)^2=\dfrac{2-\sqrt{3}}{4}$
et
$\left(\dfrac{\sqrt{6}-\sqrt{2}}{4}\right)^2=\dfrac{6+2-2\sqrt{12}}{16}=\dfrac{2-\sqrt{3}}{4}$.
Les carrés des deux nombres sont donc égaux.
De plus les deux nombres sont positifs puisqu’une racine carré est toujours positif et $\sqrt{6}>\sqrt{2}$.
Par conséquent : $\dfrac{\sqrt{2-\sqrt{3}}}{2}=\dfrac{\sqrt{6}-\sqrt{2}}{4}$.
$\quad$
- Vues: 35067
