Suites, le cours
Chapitre 1 : Les suites numériques
1. Définition d'une suite
1.1. Définition
Une suite numérique est une fonction de $\mathbb{N}$dans $\mathbb{R}$, définie à partir d'un certain rang $n_0 \in \mathbb{N}$.
La notation $\left( u_n \right) $ désigne la suite en tant qu'objet mathématique (que l'on note parfois tout simplement $u$) et $u_n$ désigne l'image de l'entier $n$
(appelé encore terme d'indice $n$ de la suite $\left( u_n \right) $), terme que l'on pourrait noter $u(n)$ mais l'usage en a voulu autrement.
Certaines suites ne sont définies qu'à partir d'un certain rang, comme par exemple :
$u_n = \dfrac{1}{n}$ définie pour $n \in \mathbb{N}^{\star} $ et $v_n =\sqrt{ n - 3}$ définie pour $n\geq 3$.
Notons que le domaine de définition est nécessairement du type $[n_0, +\infty[$ où $n_0 \in \mathbb{N}$. Il faut bien comprendre qu'il y a de multiples façons de définir une suite. Nous en rencontrerons principalement de deux types.
Celles qui sont définies par une "relation de récurrence" et la donnée d'un ou plusieurs termes initiaux comme par exemple $u_{n+2} = u_{n+1} + u_n$ et $u_0 = 0 ; u_1 = 1$ (suite de Fibonacci). Et celles qui sont définies explicitement "en fonction de $n$" comme les deux exemples cités juste au-dessus. Les stratégies pour étudier les suites dépendront justement de leur type.
Techniques fonctionnelles pour les suites de la forme $u_n = f(n)$ et techniques de récurrence pour les suites récurrentes.
2. Sens de variation (ou monotonie) d'une suite
2.1. Définition
Soit $\left( u_n \right) $ une suite de nombres réels. On dit que :
· La suite $\left( u_n \right) $ est croissante (à partir du rang $n_0$) lorsque $u_{n+1}\geq u_n$ pour tout entier $n\geq n_0$.
· La suite $\left( u_n \right) $est strictement croissante (à partir du rang $n_0$) lorsque $u_{n+1} > u_n$ pour tout entier $n\geq n_0$.
· La suite $\left( u_n \right) $ est décroissante (à partir du rang $n_0$) lorsque $u_{n+1}\leq u_n$ pour tout entier $n\geq n_0$.
· La suite $\left( u_n \right) $ est strictement décroissante (à partir du rang $n_0$) lorsque $ u_{n+1}<u_n$ pour tout entier $n\geq n_0$.
· La suite $\left( u_n \right) $ est monotone (à partir du rang $n_0$) si elle est croissante ou décroissante à partir du rang $n_0$.
· La suite $\left( u_n \right) $ est stationnaire s'il existe un entier $n_0$ tel que $ u_n = u_{n+1}$pour tout entier $n\geq n_0$.
· La suite $\left( u_n \right) $ est constante lorsque $ u_n= u_{n+1}$ pour tout entier n du domaine de définition de $\left( u_n \right) $.
Remarques : · Nuance entre suite stationnaire et suite constante :
notons $E$ la partie entière d'un réel (par exemple $E(\pi) = 3$) et $\left( u_n \right) $ la suite définie, pour $n \in \mathbb{N}^{\star}$, par $u_n = E\left( \dfrac{1}{n}\right)$ . On a $u_1 = E(1) = 1, u_2 = E(0,5) = 0$ puis pour tout $n\geq 2, u_n = 0$.
La suite $\left( u_n \right) $ est stationnaire (à partir du rang 2) mais non constante puisque $u_1 = 1$ et $u_2 = 0$.
· Il existe des suites qui sont ni croissantes, ni décroissantes. Par exemple : $u_n = (-1)^n$.
2.2. Techniques d'étude de la monotonie d'une suite :
2.2.1. Technique fonctionnelle :
utilisable pour les suites du type $u_n = f(n)$.
Théorème Où l'on utilise le sens de variation de la fonction associée :
Soit $\left( u_n \right) $ la suite définie par $u_n = f(n)$ où $f$ est une fonction définie sur un intervalle du type $[a ; +\infty[$ où $ a \in \mathbb{R}^+$.
Si la fonction $f$ est monotone sur $[a ; +\infty[$ alors la suite $\left( u_n \right) $ est monotone à partir du rang $E(a) + 1$ ; et possède le même sens de variation que $f$.
Démonstration : Supposons $f$ croissante sur $[a ; +\infty[$. (Les autres cas se prouvent de manière analogue) Soit $n \in [E(a) + 1 ; +\infty[ $ . Comme $f$ est croissante sur $[E(a) + 1 ; +\infty[ $, on a alors : $ u_{n+1} - u_n = f(n + 1) - f(n)\geq 0$.
Donc $\left( u_n \right) $ est croissante sur $[E(a) + 1 ; +\infty[ $. De même, la stricte monotonie de $f$ entraîne celle de $\left( u_n \right) $.
Exemple 1 : soit $\left( u_n \right) $ la suite définie, pour $n\geq 1$, par : $un =\cos\left(\dfrac{\pi}{n} \right)$. Notons $f$ la fonction définie sur $[1 ; +\infty[$ par :$f(x) =\cos\left(\dfrac{\pi}{x} \right)$.
La fonction $f$est dérivable sur $[1 ; +\infty[$ et on a : $f'(x) =\dfrac{\pi}{x^2} \sin \left(\dfrac{\pi}{x} \right)$.
On rappelle que $(\cos(u))'=-u'\sin(u)$.
Or, pour tout $x \in [1 ; +\infty[$, on a : $ \dfrac{\pi}{x} \in ]0 ; \pi]$ .
Et donc : $ \sin \left(\dfrac{\pi}{x} \right) \geq 0$ D'où : $f'(x)\geq 0$; donc $f$ est croissante sur $[1 ; +\infty[. $
En conséquence, la suite $\left( u_n \right) $ est croissante pour $n\geq 1$.
Exemple 2 : $u_n =\dfrac{2n^2+1}{n^2+5}$ .
Considérons la fonction $f$ définie sur $[0 ; +\infty[$ par : $f(x)=\dfrac{2x^2+1}{x^2+5}$.
La fonction $f$ est dérivable sur $[0 ; +\infty[$ et : $f '(x) =\dfrac{(4x)(x^2+5)-2x(2x^2+1)}{(x^2+5)^2} =\dfrac{18x }{(x^2+5)^2} $. Déjà le dénominateur étant un carré, il est strictement positif, donc $f '(x)$ a le signe du numérateur; comme on travaille sur $[0;+\infty[$ on a $f'(x)\geq 0$ .
La fonction $f$ est donc strictement croissante sur $[0 ; +\infty[$,il en découle la conclusion:
La suite $\left( u_n \right) $ est donc strictement croissante.
2.2.2. Techniques algébriques
C'est l'utilisation pure et simple de la définition :
$\left( u_n \right) $ est croissante à partir du rang $n_0 \Leftrightarrow $ pour tout $n\geq n_0$ on a $u_{n+1} - u_n\geq 0$.
Exemple 1 : $u_n = 2n + \sin n$
Étudions, pour tout entier $n$, le signe de la différence de deux termes consécutifs :
$u_{n+1} - u_n = 2(n + 1) + \sin(n + 1) - 2n - \sin n = 2 + \sin(n + 1) - \sin n$
Or : $-1\leq \sin(n + 1)\leq 1 $et $-1 \leq -\sin n\leq 1$
En ajoutant membre à membre : $-2 \leq \sin(n + 1) - \sin n \leq 2$
Par conséquent : $u_{n+1} - u_n\geq 0$
La suite $\left( u_n \right) $ est donc croissante.
Variante : soit $\left( u_n \right) $ une suite à termes STRICTEMENT POSITIFS.
Si, pour tout entier $n$, $ \dfrac{u_{n+1}}{u_n} \geq 1$ alors la suite $\left( u_n \right) $ est croissante.
Si, pour tout entier $n$, $\dfrac{u_{n+1}}{u_n} \leq 1$ alors la suite $\left( u_n \right) $ est décroissante.
Exemple 2 : $u_n = \dfrac{2^n}{n^2}$ pour $n\geq 1$.
La suite $\left( u_n \right) $ à termes STRICTEMENT POSITIFS.
Évaluons, pour tout $n\geq 1$, la situation du quotient de deux termes consécutifs par rapport à 1 :
$\dfrac{u_{n+1}}{u_n}=\dfrac{2^{n+1}}{(n+1)^2}\times \dfrac{n^2}{2^n}=\dfrac{2n^2}{(n+1)^2}$.
Recherchons s'il existe des valeurs de l'entier $n$ pour lesquelles le quotient ci-dessus est supérieur à 1 :
$ \dfrac{u_{n+1}}{u_n}\geq 1 \Leftrightarrow \dfrac{2n^2}{(n+1)^2}\geq 1 $ (1)
(1) $\Leftrightarrow 2n^2\geq (n+1)^2$ en effet , ici $n \in \mathbb{N}^{\star}$ donc $(n+1)^2>0$
(1) $n^2-2n-1\geq 0$
On calcule alors les racines du trinôme $n^2-2n-1$:
$\Delta= b^2-4ac=8$, et donc les racines de ce trinôme sont :$$n_1=\dfrac{-b-\sqrt{\Delta}}{2a} =\dfrac{2-2\sqrt 2}{2}=1-\sqrt 2 \text{ et } n_2=\dfrac{-b+\sqrt{\Delta}}{2a} =1+\sqrt 2.$$
Le trinôme étant du signe de $a$ à l'extéreur des racines et de celui de $-a$ à 'inérieur, on déduit:
$ \dfrac{u_{n+1}}{u_n}\geq 1 \Leftrightarrow n\geq 1+\sqrt 2 $ et comme $1+\sqrt 2 \approx 2.42$ , on a $ \dfrac{u_{n+1}}{u_n}\geq 1 \Leftrightarrow n\geq 3$
La suite $\left( u_n \right) $ est croissante pour $n\geq 3$.
Note : si l'on a pronostiqué le résultat (avec une calculatrice par exemple), on peut alors rédiger une solution
plus courte : pour $n > 3$, on a :$ \dfrac{u_{n+1}}{u_n}=\dfrac{2n^2}{(n+1)^2}=2\left (\dfrac{n}{n+1}\right )^2$
Or si $n\geq 3$ alors $\dfrac{1}{n} \leq \dfrac{1}{3}$
En effet : $x\mapsto \dfrac{1}{x} $ est srtictement déctoissante sur $]0;+\infty[$;
puis $1+\dfrac{1}{n}\leq 1+\dfrac{1}{3}$ soit $\dfrac{n+1}{n}\leq \dfrac{4}{3}$
puis par passage à l'inverse $ \dfrac{n}{n+1}\geq \dfrac{3}{4}$,
en élévant au carrré $x\mapsto x^2$ est strictement croissante sur $\mathbb{R}^+$,
on a donc : $\left (\dfrac{n}{n+1}\right )^2\geq \dfrac{9}{16} $ puis en multipliant par $2$ qui est strictement psitif ;
il vient : $ 2\times \left (\dfrac{n}{n+1}\right )^2\geq \dfrac{18}{16}$; et donc $ \dfrac{u_{n+1}}{u_n}\geq 1$.
Exemple 3 : cas d'une suite définie par une somme : $u_n=\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\ldots \ldots+\dfrac{1}{n}^2$ pour tout $n \in \mathbb{N}^{\star}$
On a, pour tout $n \in \mathbb{N}^{\star} : u_{n+1} - u_n = 1/ (n +1)^2$
Donc pour tout $n \in \mathbb{N}^{\star}: u_{n+1} - u_n > 0$
Donc ($u_n)$ est strictement croissante.
2.2.3. Technique par récurrence : pratique pour les suites du type $ u_{n+1} =f\left( u_n \right) $.
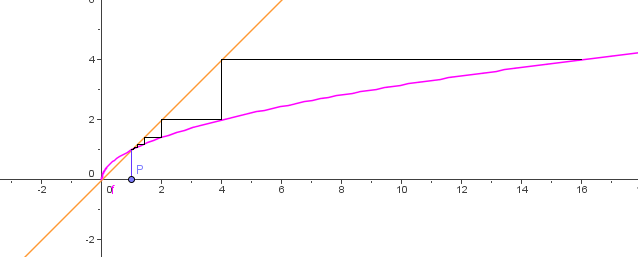
Exemple : Soit $\left( u_n \right) $ la suite définie par : $u_0=16$ et $u_{n+1}=\sqrt{u_n} $
Démontrons par récurrence que cette suite est décroissante.
On considère la propriété $(P)$ définie pour $n in \mathbb{N}$ par :$P(n) : 0\leq u_{n+1}\leq u_n$
· On a $u_1 = 4$ donc $0 \leq u_1 \leq u_0$, d'où $P(0)$. Donc $P$ est initialisée au rang 0.
· Montrons que $P$ est héréditaire à partir du rang 0.
Soit $n in \mathbb{N}$. Supposons $P(n) : 0\leq u_{n+1}\leq u_n$
Alors, par croissance de l'application $x\mapsto \sqrt x$ sur $\mathbb{R}^+$, nous avons :
$\sqrt 0\leq \sqrt{u_{n+1}}\leq \sqrt{u_n}$
d'où $ 0 \leq u_{n+2}\leq u_{n+1}$
D'où $P(n + 1)$.
La propriété $P$ est initialisée au rang 0 et héréditaire à partir du rang 0, donc d'après le principe de raisonnement par récurrence, elle est vraie à tout rang $n$:
pour tout $n\geq 0$, on a $u_{n+1} \leq u_n$
La suite $\left( u_n \right) $ est bien décroissante.
Une représentation graphique de cette suite:
3. Suite majorée, suite minorée, suite bornée
3.1. Définition
Une suite $\left( u_n \right) $ est majorée lorsqu'il existe un réel $M$ tel que $u_n \leq M$ pour tout entier $n$.
Une suite $\left( u_n \right) $ est minorée lorsqu'il existe un réel $m$ tel que $u_n\geq m$ pour tout entier $n$.
Une suite $\left( u_n \right) $ est bornée lorsqu'elle est minorée et majorée :
il existe des réels $m$ et $M$ tels que $m \leq u_n \leq M$ pour tout entier $n$.
Remarque :
Une suite $\left( u_n \right) $ est bornée si et seulement si il existe un réel $M$ tel que $|un| \leq M$ pour tout entier $n$.
En effet, si $\left( u_n \right) $ est bornée, il existe des réels $a$ et $b$ tels que pour tout entier $n$ on ait :
$a \leq u_n \leq b$
Notons $M = max(|a| ; |b|)$. Comme $b \leq |b| \leq M$ et $-M \leq -|a| \leq a$, on obtient :
$-M \leq u_n \leq M$
D'où : $|u_n| \leq M$
La réciproque est évidente.
3.2. Techniques pour prouver qu'une suite est majorée (ou minorée ou bornée)
3.2.1. Technique algébrique : manipulation d'inégalités
Exemple 1 : $u_n =\dfrac{(-1)^n + \sin n }{n^2}$ , pour $n \in \mathbb{N}^{\star}$.
On a : $ -1\leq \sin n \leq 1$ et $-1\leq \sin n \leq 1$ donc en ajoutant membre à membre ces deux inégalités de même sens, il vient:$-2 \leq (-1)^n + \sin n \leq 2 $ et $0 \leq \dfrac{1}{n}^2\leq 1$
D'où : $-2 \leq u_n \leq 2$
La suite $\left( u_n \right) $ est bornée.
Exemple 2 : $u_n = \displaystyle\sum_{k=1} ^ n \dfrac{1}{k^2} $ , pour $n \in \mathbb{N}^{\star}$
Montrer que $\left( u_n \right) $ est majorée par 2.
En remarquant que, pour $k\geq 2 : \dfrac{1}{k^2}\leq \dfrac{1}{k(k-1)}\leq \dfrac{1}{k-1}- \dfrac{1}{k}$.
On a : $u_n = 1 +\dfrac{1}{2}^2+\dfrac{1}{3}^2+........+\dfrac{1}{n}^2$
On écrit successivement: en remplaçant $k$ par :$2;3; .......;n-1;n$ dans la relation $(R) : \dfrac{1}{k^2}\leq \dfrac{1}{k-1}- \dfrac{1}{k}$.
| $k=2$ | donne | $\dfrac{1}{2} ^2\leq 1 - \dfrac{1}{2}$ |
| $k=3$ | donne | $\dfrac{1}{3} ^2\leq \dfrac{1}{2} - \dfrac{1}{3}$ |
| $k=4$ | donne | $\dfrac{1}{4} ^2\leq \dfrac{1}{3} - \dfrac{1}{4}$ |
| $k=n-1$ | donne | $\dfrac{1}{(n-1) ^2} \leq \dfrac{1}{n-2} - \dfrac{1}{n-1}$ |
| $k=n$ | donne | $\dfrac{1}{n ^2} \leq \dfrac{1}{n-1} - \dfrac{1}{n-2}$ |
On ajoute ces $n-1$ inégalités, d'où $ \dfrac{1}{2}^2+\dfrac{1}{3}^2+........+\dfrac{1}{n}^2\leq 1-\dfrac{1}{n}$
Puis $1+ \dfrac{1}{2}^2+\dfrac{1}{3}^2+........+\dfrac{1}{n}^2\leq 2-\dfrac{1}{n}$ ;
Soit $u_n\leq 2$
On a ainsi prouvé que $\left( u_n \right)$est majorée par $2$.
Exemple 3 :Soit $\left( u_n \right) $la suite définie par:$u_n = \displaystyle\sum_{k=0} ^ n \dfrac{1}{k!} $
Montrer que $\left( u_n \right) $ est majorée par 3.
Montrons tout d'abord, par récurrence, la propriété $P$, définie pour $k \in \mathbb{N}^{\star}$, par :
$P(k) : k!\geq 2^{k -1}$
· On a évidemment $P(1)$, en effet $1!=1$ et $2^{1 -1}=1$. La propriété $P$ est initialisée au rang 1.
· Montrons que $P$ est héréditaire à partir du rang 1.
Soit $k \in N^{\star}$. Supposons $P(k) : k!\geq 2^{k -1}$
Alors on a : $(k + 1)! = (k + 1) \times k!\geq (k + 1) \times 2^{k -1}$
Et comme $k\geq 1$on déduit $(k + 1)\geq 2$ : puis $(k + 1)!\geq 2^ k$, Ce qui est $P(k + 1)$.
Du principe de raisonnement par récurrence, on déduit :
$k!\geq 2^{k -1} $ pour tout $k\geq 1$.
On peut donc écrire : $u_n = 1 + sum_{k=1}^n \dfrac{1}{k!}$.
D'après la propriété établie par récurrence, on a pour tout $k\geq 1$: $k!\geq 2^{k -1} $;
en prenant les inverses il vient pour tout $k\geq 1$ $(Q) : \dfrac{1}{k!}\leq (\dfrac{1}{2})^(k-1)$.
On écrit successivement: en remplaçant $k$ par :$1;2;3; .......;n-1;n$ dans la relation $(Q)$ :
| $k=1$ | donne | $\dfrac{1}{1!} \leq \left(\dfrac{1}{2}\right)^0$ |
| $k=2$ | donne | $\dfrac{1}{2!} \leq \left(\dfrac{1}{2}\right)^1$ |
| $k=3$ | donne | $\dfrac{1}{3!} \leq \left(\dfrac{1}{2}\right)^2$ |
| $k=n-1$ | donne | $\dfrac{1}{(n-1) !} \leq \left(\dfrac{1}{2}\right)^{n-2}$ |
| $k=n$ | donne | $\dfrac{1}{n !}\leq \left(\dfrac{1}{2} \right)^{n-1}$ |
On ajoute membre à membre ces $n$ inégalités, d'où $ \dfrac{1}{1!}+\dfrac{1}{2!}+\dfrac{1}{3!}+........+\dfrac{1}{n!}\leq 1+\left (\dfrac{1}{2}\right)+\left (\dfrac{1}{2}\right)^2+.....+\left(\dfrac{1}{2} \right)^{n-1}$
On reconnaît une somme de $n$ termes consécutifs d'une suite géométrique de raison $\dfrac{1}{2}$, d'où :
D'après le cours : Si $q\neq 1$alors $1+q+q^ 2+q^3+........+q^n=\dfrac{1- \text{ raison } ^ {\text{ Nombre de termes}}}{1- \text{ raison }} \times\text{ premier terme} $.
Ici $ 1+\left (\dfrac{1}{2}\right)+\left (\dfrac{1}{2}\right)^2+.....+\left(\dfrac{1}{2} \right)^{n-1}=\dfrac{1-\left(\dfrac{1}{2}\right )^n}{1-\dfrac{1}{2}} \times 1=2 \times\left(1-(\dfrac{1}{2})^n\right)$
On a donc $ \dfrac{1}{1!}+\dfrac{1}{2!}+\dfrac{1}{3!}+........+\dfrac{1}{n!}\leq 2 \times(1-(\dfrac{1}{2})^n)$
On ajoute $1$: $ 1+\dfrac{1}{1!}+\dfrac{1}{2!}+\dfrac{1}{3!}+........+\dfrac{1}{n!}\leq 3-2 \times(\dfrac{1}{2})^n$
On a ainsi établi que pour tout $ n \in \mathbb{N}$ on a $u_n\leq 3$.
3.2.2. Technique fonctionnelle
Exemple : $u_n = \dfrac{2 n^2+1}{n^2+5}$
Considérons la fonction $f$ définie sur $[0 ; +\infty[$ par : $f(x)=\dfrac{2 x^2+1}{x^2+5}$
On a déjà vu, plus haut, que $f$ est croissante sur $[0 ; +\infty[$.
Par ailleurs, on a $f(0) = \dfrac{1}{5}$ et$\lim\limits_{x \to +\infty}f(x)=2$.
On duit donc que pour tout $x \in [0;+\infty[$ on a $\dfrac{1}{5}\leq f(x)\leq 2$;
et donc en particulier pour tout $n \in \mathbb{N}$ on a : $\dfrac{1}{5}\leq f(n)\leq 2$ ce qui fournit $\dfrac{1}{5}\leq u_n\leq 2$
La suite $\left( u_n \right) $ est donc bornée : majorée par $2$ et minorée par $\dfrac{1}{5}$
3.3.3. Technique par récurrence
Exemple : $u_{n+1} = \sqrt{6 + u_n}$ avec $u_0 = 0$
On considère la propriété $P$, définie pour $n \in \mathbb{N}$, par :
$P(n) : 0 \leq u_n \leq 3$
· Par hypothèse, on a $P(0)$; en effet $0\leq u_0\leq 3$. La propriété est initialisée au rang 0.
· Montrons que $P$ est héréditaire à partir du rang 0.
Soit $nin \mathbb{N}$. Supposons $P(n)$ : $0 \leq un\leq 3$
Alors, en ajoutant 6 :$ 6 \leq 6 + u_n \leq 9$
Par passage à la racine carrée (qui est une fonction croissante sur $\mathbb{R}^{+}$) :
$\sqrt6\leq \sqrt{ 6 + u_n}\leq 3$
Donc :$0 \leq u_{n+1}\leq 3$
Conclusion : pour tout entier $n\geq 0$ , on a : $0 \leq u_n \leq 3$
On peut aussi retrouver ce résultat par la méthode algébrique. (Manipulation d'inégalités)
4. Comportement asymptotique d'une suite
4.1. Définition Suite convergente
On dit qu'une suite converge (ou admet une limite finie) lorsqu'il existe un réel $l$ tel que :
tout intervalle ouvert $I$ centré en $l$ contient tous les termes de la suite à partir d'un certain rang.
Lorsque $\left( u_n \right) $ converge vers $l$, on note alors : $l = \lim\limits_{n \to +\infty} u_n$.
Une suite non convergente est appelée suite divergente.
En formulant différemment cette définition, on obtient plusieurs variantes toutes équivalentes :
$\left( u_n \right) $ converge lorsqu'il existe un réel $l$ tel que :
1) Tout intervalle $ I = ]l - \epsilon, l + \epsilon[ (\epsilon \in \mathbb{R}_+^{\star})$ contient tous les termes de la suite à partir d'un certain rang.
2) Pour tout réel $\epsilon \in \mathbb{R}_+^{\star}$ , il existe un rang $N$ à partir duquel tous les $u_n$ vérifient $u_n \in ]l - \epsilon, l + \epsilon[$.
3) Pour tout réel $\epsilon \in \mathbb{R}_+^{\star}$, il existe un rang $N$ tel que pour tout indice $n$, on ait : $n\geq N \Rightarrow|u_n - l| < \epsilon$.
Graphiquement, cela se traduit ainsi :
Quelle que soit la largeur de la bande horizontale choisie, il existe un rang (ou un indice) à partir duquel tous les points de la représentation graphique de la suite sont situés dans cette bande.
Illustration avec la suite $\left( u_n \right) $ définie par :$u_n=\dfrac{3n+5(-1)^n}{2n}$:
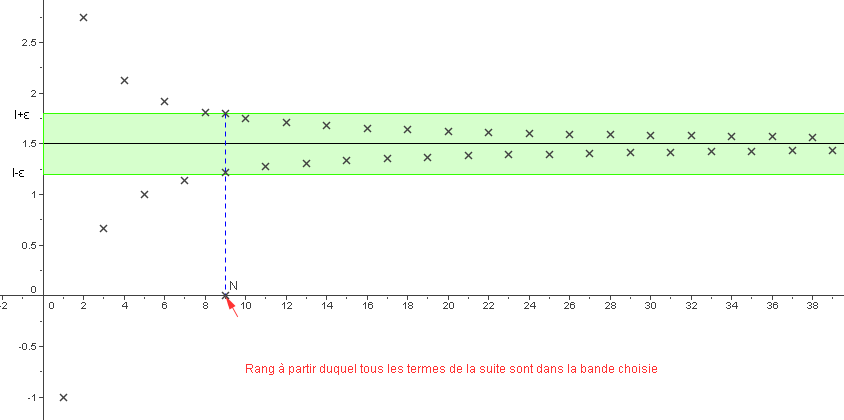
Sur cet exemple, le graphique permet de conjecturer que la suite $\left( u_n \right) $ converge vers $\dfrac{3}{2}$ , ce que le théorème des
gendarmes confirmera. (Voir 6.2.)
Remarque : on peut très bien travailler avec un intervalle $I$ qui est fermé (et donc avec des inégalités larges).
4.2. Propriété Unicité de la limite
Si $\left( u_n \right) $ converge, alors sa limite $l$ est unique.
Démonstration
Raisonnons par l'absurde. Supposons que la suite $\left( u_n \right) $ admette deux limites distinctes $l_1$ et $l_2$ avec $l_1 < l_2$.
Notons $d = l_2 - l_1$.
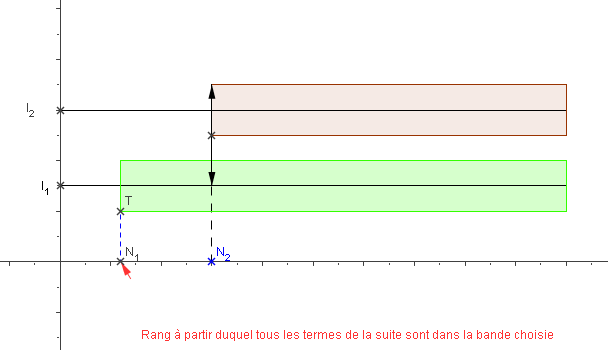
Comme $\left( u_n \right) $ converge vers $l_1$, à partir d'un certain rang $N_1$, tous les termes de la suite sont dans l'intervalle ouvert $I_1$ de centre $l_1$ et de rayon $\dfrac{d}{3}$ .
De même, comme $\left( u_n \right) $ converge vers $l_2$, à partir d'un certain rang $N_2$, tous les termes de la suite sont dans l'intervalle ouvert $I_2$ de centre $l_2$ et de rayon $\dfrac{d}{3}$ .
Donc à partir du rang $N = max(N_1, N_2)$, tous les termes de la suite sont simultanément dans $I_1$ et $I_2$. Or ces deux
intervalles sont disjoints (ils ne se chevauchent pas). Ce qui n'est pas possible.
Ceci prouve l'unicité de la limite.
Illustration : Comment, à partir du rang $N_1$, tous les termes de la suite pourraient-ils se situer dans ces deux "tuyaux" ?
4.3. Propriété
Si $\left( u_n \right) $ converge, alors $\left( u_n \right) $ est bornée.
Démonstration
Notons $l$ la limite de la suite $\left( u_n \right) $ et I l'intervalle $]l - 1, l + 1[$. $I $ est bien un intervalle ouvert centré en $l$.
Comme $\left( u_n \right) $ converge, à partir d'un certain rang $N$, tous les termes de la suite $\left( u_n \right) $ sont dans $I$.
Autrement dit : $n\geq N \Rightarrow l - 1 < u_n < l + 1$
· Si $N = 0$, alors c'est fini, $\left( u_n \right) $ est bornée par les réels $l - 1$ et $l + 1$.
· Si $N\geq 1$, alors notons$ A$ l'ensemble ${u_0, ... , u_{N-1}, l - 1, l + 1}, M$ le plus grand élément de $A$ et $m$ son plus petit élément. Ainsi $\left( u_n \right) $ est bornée par les réels $m$ et $M$.
Étudions maintenant un cas spécial de suites divergentes :
4.4. Définition Suite divergente vers $+\infty$
On dit qu'une suite diverge vers $+\infty$ lorsque :
tout intervalle ouvert du type $]A, +\infty[$ (où $A > 0$) contient tous les termes de la suite à partir d'un certain rang.
En formulant différemment cette définition, on obtient plusieurs variantes toutes équivalentes :
$\left( u_n \right) $ diverge vers $+\infty$ lorsque :
1) Pour tout $A \in \mathbb{R}_+^{\star}$ , l'intervalle $]A, +\infty[$ contient tous les termes de la suite à partir d'un certain rang.
2) Pour tout $A \in \mathbb{R}_+^{\star}$, il existe un rang $N$ tel que pour tout indice $N$, on ait :$ n\geq N \Rightarrow u_n > A$.
On définit de même la divergence vers $-\infty$ à l'aide d'intervalles du type $]-\infty, A[$.
4.5. Quelques limites de références
Donnons, sans plus tarder, quelques limites de référence :
$\lim\limits_{n \to +\infty} \sqrt{n}=+\infty$ $\lim\limits_{n \to +\infty} n^2=+\infty$ $\lim\limits_{n \to +\infty} \dfrac{1}{n}=0$ $\lim\limits_{n \to +\infty} \dfrac{1}{n^2}=0$
Démontrons quelques uns de ces résultats (hors programme)
·$ \lim\limits_{n \to +\infty} \sqrt{n}=+\infty$:
Soit $A \in \mathbb{R}+^{\star}$. Montrons que l'intervalle $]A;+\infty[$ contient tous les nombres $\sqrt{n}$ à partir d'un certain rang.
Comme $A > 0$, on a : $n > A \Rightarrow n > A^ 2$
Posons $N = E(A^2) + 1$. Ainsi, à partir du rang $N$, on a $n \in ]A;+\infty[$, ce qui prouve $ \lim\limits_{n \to +\infty} \sqrt{n}=+\infty$.
· $\lim\limits_{n \to +\infty} \dfrac{1}{n}=0$
Soit $\epsilon \in \mathbb{R}+^{\star}$ et $I = ]-\epsilon, \epsilon[$ (intervalle ouvert centré en 0).
Montrons que $I$ contient tous les nombres $\dfrac{1}{n}$ à partir d'un certain rang.
Or : $0 < \dfrac{1}{n}<\epsilon \Rightarrow n >\dfrac{1}{\epsilon}>0$
Posons $N = E(1/\epsilon) + 1$. Ainsi, à partir du rang $N$, on a $\dfrac{1}{n} \in I$, ce qui prouve $\lim\limits_{n \to +\infty} \dfrac{1}{n}=0$.
Les autres résultats se montrent de manière analogue et il n'est pas intéressant de tous les détailler ici.
Précisons plutôt un résultat plus fort :
Soit $f$ une fonction définie sur un intervalle du type $[a, +\infty[$ où $a \in \mathbb{R}^+$ et $\left( u_n \right) $ la suite définie par $u_n = f(n)$
. Si $\lim\limits_{x \to +\infty}f(x)=l$ alors $\lim\limits_{n \to +\infty} u_n=l$
. Si $\lim\limits_{x \to +\infty}f(x)=+\infty$ alors $\lim\limits_{n \to +\infty} u_n=+\infty$. Si $\lim\limits_{x \to +\infty}f(x)=-\infty$ alors $ \lim\limits_{n \to +\infty} u_n=-\infty$
En conséquence, on récupère tous les théorèmes sur les règles opératoires sur les limites de fonctions.
Exemple : étudier la limite de la suite $\left( u_n \right) $ définie par : $u_n =\dfrac{5n^2-3n+1}{4n^2+1}$
Écrivons : $u_n =\dfrac{n^2\left (5-\dfrac{3}{n}+\dfrac{1}{n}^2\right )}{n^2\left (4+\dfrac{1}{n}^2\right )}=\dfrac{5-\dfrac{3}{n}+\dfrac{1}{n}^2}{4+\dfrac{1}{n}^2}$
Or :$ \lim\limits_{n \to +\infty} \dfrac{1}{n}=0$ et $ \lim\limits_{n \to +\infty} \dfrac{1}{n}^2=0$
On a donc $\left.\begin{array}{l} \lim\limits_{n \to +\infty}~\left (5-\dfrac{3}{n}+\dfrac{1}{n}^2\right )=5\\ \lim\limits_{n \to +\infty}~4+\dfrac{1}{n}^2=4 \end{array}\right\}$ par quotient on obtient: $\lim\limits_{n \to +\infty}u_n=\dfrac{5}{4}$.
On verra justement au paragraphe 5 toutes les règles opératoires sur les limites de suites.
4.6. Remarque : autres cas de divergence
Il existe des suites divergentes qui ne divergent pas vers $+\infty$ (ou $-\infty$).
C'est par exemple le cas de : $u_n = (-1)^n$
Preuve :
On fait ici un raisonnement par l'absurde:
Supposons, au contraire, que la suite de terme général $(-1)^n$ converge vers un certain entier $l$.
Soit $I =\left]l-\dfrac{1}{2} 1; l+\dfrac{1}{2}\right[$ . $I$ est un intervalle ouvert centré en $l$.
D'après notre hypothèse, il existe un rang $N$ à partir duquel, on aura :$ (-1)^ n \in I$
Autrement dit : $- \dfrac{1}{2}<(-1)^n-l<\dfrac{1}{2}$
Or, pour $n$ pair, cela donne : $- \dfrac{1}{2}<1-l<\dfrac{1}{2}$ soit $-\dfrac{3}{2}<-l<-\dfrac{1}{2}$ puis $l \in ]\dfrac{1}{2};\dfrac{3}{2}[$
Et pour n impair :$- \dfrac{1}{2}<-1-l<\dfrac{1}{2}$ soit $\dfrac{1}{2}<-l<\dfrac{3}{2}$ puis $l \in ]-\dfrac{3}{2};-\dfrac{1}{2}[$
D'où une contradiction. Donc la suite considérée diverge.
Exercice : démontrer que les suites $(\sin n)$ et $(\cos n)$ divergent.
Supposons que la suite $(\cos n)$ converge vers un certain réel $l \in [-1, 1]$.
On sait que : $\cos(n + 1) = \cos n \cos 1 - \sin n \sin 1$
Les suites $(\cos(n + 1))$ et $(\cos n \cos 1)$ ont, par hypothèse, une limite.
On en déduit, par différence que la suite $(\sin n \sin 1)$ aussi.
Ayant $\sin 1$ est non nul, de $\cos(n + 1) = \cos n \cos 1 - \sin n \sin 1$ on déduit : $\sin n=(\cos n \cos 1-\cos(n+1))/(\sin 1)$ et donc la suite $(\sin n)$ converge vers un certain réel $k = (l(\cos1 -1))/(\sin 1)$.
Ce réel k est non nul car $\cos 1 \neq 1$.
En outre, on sait que : $\sin(2n) = 2 \cos n \sin n$; en passant à la limite, on aurait : $k = 2 l k$
d'où $k = 2 l k \Leftrightarrow k-2lk=0 \Leftrightarrow k(1-2l)=0$ .Et comme $k\neq 0 $: on a alors $l=\dfrac{1}{2}$
Par ailleurs, on sait que : $\cos(2n) = 2\cos^2 n - 1$; en passant à la limite, on aurait : $l =2 l^2 - 1$
On a alors $2l^2-l-1=0$; or $l_1=1$est une racine évidente de ce trinôme, et donc $l_1l_2=c/a$ donne $ l_2=-1$.
On avait obtenu par ailleurs $l=\dfrac{1}{2}$, il s'en suit une contradiction.
Les suites de terme général $\sin n$ et $\cos n$ divergent.
4.7. Théorème de la limite monotone
Toute suite croissante et majorée converge. Toute suite décroissante et minorée converge.
Applications :
· La suite $\left( u_n \right) $ définie par $u_n = \displaystyle\sum_{k=1}^n \dfrac{1}{k^2}$ , pour $n\geq 1$ est croissante et majorée (voir plus haut) donc
convergente. (Sa limite est difficile à déterminer, elle vaut $\dfrac{\pi^2}{6} $)
· La suite $\left( u_n \right) $ définie par $u_n =\displaystyle\sum_{k=1}^n \dfrac{1}{k!}$ est croissante et majorée donc convergente. On montrera que sa limite est nombre irrationnel. (Nombre $e$ qui sera défini ultérieurement).
5. Règles opératoires sur les limites d'une suite
Soient $(a_n)$ et $(b_n)$ deux suites qui admettent pour limite $a$ et $ b$ ($a$ et $b$ sont des réels ou $+\infty$ ou $-\infty$)
5.1. Cas de la somme :
|
$\lim\limits_{n \to +\infty} b_n= \rightarrow $ $\lim\limits_{n \to +\infty} a_n= \downarrow $ |
$b \in \mathbb{R}$
|
$+\infty$
|
$-\infty$
|
|
$a \in \mathbb{R}$
|
$a+b$
|
$+\infty$
|
$-\infty$
|
|
$+\infty$
|
$+\infty$
|
$+\infty$
|
?
|
|
$-\infty$
|
$-\infty$
|
?
|
$-\infty$
|
5.2. Cas du produit :
comment déterminer $\lim\limits_{n \to +\infty} (a_nb_n)$?
|
$\lim\limits_{n \to +\infty} b_n= \rightarrow $ $\lim\limits_{n \to +\infty} a_n= \downarrow $ |
$-\infty$
|
$b<0$
|
$0$
|
$b>0$
|
$+\infty$
|
|
$-\infty$
|
$+\infty$
|
$+\infty$
|
?
|
$-\infty$
|
$-\infty$
|
|
$a<0$
|
$+\infty$
|
$ a b$
|
$0$
|
$ab$
|
$-\infty$
|
|
$0$
|
?
|
$0$
|
$0$
|
$0$
|
?
|
|
$a>0$
|
$-\infty$
|
$ab$
|
$0$
|
$ab$
|
$+\infty$
|
|
$+\infty$
|
$-\infty$
|
$-\infty$
|
?
|
$+\infty$
|
$+\infty$
|
5.3. Cas du quotient :
comment déterminer $\lim\limits_{n \to +\infty} ((a_n)/(b_n))$?
|
$\lim\limits_{n \to +\infty} b_n= \rightarrow $ $\lim\limits_{n \to +\infty} a_n= \downarrow $ |
$-\infty$
|
$b<0$
|
$0^-$
|
$0^+$
|
$b>0$
|
$+\infty$
|
|
$-\infty$
|
?
|
$+\infty$
|
$+\infty$
|
$-\infty$
|
$-\infty$
|
?
|
|
$a<0$
|
$0$
|
$ a/ b$
|
$+\infty$
|
$-\infty$
|
$a/b$
|
$0$
|
|
$0$
|
$0$
|
$0$
|
?
|
?
|
$0$
|
$0$
|
|
$a>0$
|
$0$
|
$a/b$
|
$-\infty$
|
$+\infty$
|
$a/b$
|
$0$
|
|
$+\infty$
|
?
|
$-\infty$
|
$-\infty$
|
$+\infty$
|
$+\infty$
|
?
|
Les points d'interrogation (?) signalent les cas indéterminés, pour lesquels une étude spécifique doit être menée pour déterminer l'éventuelle limite.
Il faut bien être conscient que tous les résultats de ces tableaux se démontrent. (Tous ne sont d'ailleurs pas évidents).
Donnons quelques unes de ces démonstrations :
Limite de la somme de deux suites convergentes égale à la somme des limites :Soit $\epsilon \in \mathbb{R}+^{\star}$ .
Comme $(a_n)$ converge vers $a$, à partir d'un certain rang $N_1$, on a : $a_n \in ]a - \dfrac{2}{\epsilon}; a + \dfrac{2}{\epsilon}[$; autrement dit : $|a_n-a|<\dfrac{\epsilon}{2}$.
Comme $(b_n)$ converge vers $b$, à partir d'un certain rang $N_2$, on a : $b_n in ]b - \dfrac{2}{\epsilon}; b + \dfrac{2}{\epsilon}[$; autrement dit : $|b_n-b|<\dfrac{\epsilon}{2}$.
On a donc pour $N>max(N_1,N_2)$: $|a_n+b_n-(a+b)|= |a_n-a+b_n-b|\leq |a_n-a|+|b_n-b|\leq \dfrac{\epsilon}{2}+\dfrac{\epsilon}{2}$.
Donc si $N>max(N_1,N_2)$: $|a_n+b_n-(a+b)|\leq \epsilon$, autrement dit :$a_n+b_n \in ]a+b-\epsilon;a+b+\epsilon[$.
Ceci prouve que $(a_n+b_n) $ converge vers $a+b$.
Limite du produit de deux suites convergentes égale au produit des limites :Soit $\epsilon \in \mathbb{R}+^{\star}$ . L'idée est d'écrire : $a_nb_n - ab = (a_n - a)b_n + (b_n - b)a$
Comme la suite $(a_n - a)$ converge vers 0 et que la suite $(b_n)$ est bornée (puisque convergente), on en déduit (voir
exercice section 4.3) que la suite $((a_n - a)b_n)$ converge vers 0. De même, la suite $((b_n - b)a)$ converge vers 0.
Donc la suite $(a_nb_n)$ converge vers $ab$.
Les autres règles opératoires sur les limites se démontrent aussi. On ne les donne pas toutes ici pour ne pas
alourdir l'exposé.
Quelques exemples d'étude de cas indéterminés :
Cas $ \infty- \infty $:
$u_n =\sqrt{ n +1} -\sqrt{ n }$
On écrit : $u_n = \dfrac{\left (\sqrt{ n +1} -\sqrt{ n }\right )\left (\sqrt{ n +1}+\sqrt{ n } \right )}{\left (\sqrt{ n +1}+\sqrt{ n } \right )}= \dfrac{1}{\left (\sqrt{ n +1}+\sqrt{ n } \right )}$
$\left.\begin{array}{l} \lim\limits_{n \to +\infty}\sqrt{n+1}=+\infty\\ \lim\limits_{n \to +\infty} \sqrt{n}=+\infty\end{array}\right\}$ par somme on obtient: $\lim\limits_{n \to+\infty} \left (\sqrt{ n +1}+\sqrt{ n } \right )=+\infty$ puis par inverse :$ \lim\limits_{n \to +\infty} \dfrac{1}{\left (\sqrt{ n +1}+\sqrt{ n } \right )}=0$.
Cas $0 \times \infty$:
$u_n =n \sin\left (\dfrac{1}{n}\right )$; comme $\left.\begin{array}{l} \lim\limits_{n \to +\infty} \dfrac{1}{n}=0\\ \lim\limits_{t \to 0 }~\sin(t)=0 \end{array}\right\}$ par par composée: $\lim\limits_{n \to +\infty} \sin(\dfrac{1}{n})=0$
Par ailleurs $\lim\limits_{n \to +\infty} n=+\infty$, on débouche donc sur la forme indéterminée: $0 \times \infty$.
Pour lever l'indétermination, on écrit :$u_n =\dfrac{\sin\left (\dfrac{1}{n}\right )}{\dfrac{1}{n}}$ $\left.\begin{array}{l} \lim\limits_{n \to +\infty}~\dfrac{1}{n}=O\\ \lim\limits_{t \to 0}~\dfrac{\sin t}{t}=1 \end{array}\right\}$ par composée on obtient: $\lim\limits_{n \to +\infty}n \sin\left (\dfrac{1}{n}\right )=1$
Cas $0 / 0$ :
$ u_n =\dfrac{1-\cos\left (\dfrac{1}{n}\right )}{\dfrac{1}{n}^2}$L'idée est de partir de la limite suivante : $\lim\limits_{x \to 0}~\dfrac{\sin x}{x}=1$
En conséquence : $\lim\limits_{x \to 0} \left ( \dfrac{\sin x}{x} \right ) ^2=1$.
Or :
$\left ( \dfrac{\sin x}{x} \right ) ^2= \dfrac{\sin^2x}{x^2} = \dfrac{1-\cos^2x}{x^2} =\dfrac{\left (1-\cos x\right )\left (1+\cos x \right )}{x^2} $;
on en déduit donc :$\dfrac{1-\cos x}{x^2} = \dfrac{1}{1+\cos x} \times \left ( \dfrac{\sin x}{x} \right ) ^2$
Ayant $\lim\limits_{x \to 0}\dfrac{1}{1+\cos x}=\dfrac{1}{2}$; on a donc :$\lim\limits_{x \to 0} \dfrac{1}{1+\cos x} \times \left ( \dfrac{\sin x}{x} \right ) ^2=\dfrac{1}{2}$, puis $\lim\limits_{x \to 0}\dfrac{1-\cos x}{x^2}=\dfrac{1}{2}$
Cas $\dfrac{\infty}{\infty} $ : un exemple a déjà été donné plus haut (section 4.5.)
5.4. Linéarité de la limite
En combinant les résultats sur la somme et le produit (par un scalaire, c'est-à-dire une constante) pour les suites convergentes, on obtient :$ \lim\limits_{n \to+\infty}(au_n + bv_n) = a \lim\limits_{n \to+\infty}u_n + b \lim\limits_{n \to+\infty}v_n $
6. Quelques théorèmes de comparaison et d'encadrement
6.1. Comparaison par rapport à une suite divergente
· Si $\left( u_n \right) $ diverge vers $+\infty$ alors $(v_n)$ aussi.
· Si $(v_n)$ diverge vers $-\infty$ alors $\left( u_n \right) $ aussi.
Fixons $A \in \mathbb{R}+^{\star}$. Supposons que $\left( u_n \right) $ diverge vers $+\infty$. Alors, à partir d'un certain rang $N$, on a :
$u_n\geq A$; et comme $v_n\geq u_n$, on aura aussi : $v_n\geq A$.
Donc $(v_n)$ diverge vers $+\infty$.
Le deuxième point se démontre de manière analogue.
Étudier la limite de la suite $\left( u_n \right) $ définie, pour tout $n \in \mathbb{N}$, par : $ u_n = 2\cos n + 3 \times(-1)^n - 3n$
On a pour tout $n \in \mathbb{N}$: $-1\leq \cos n\leq 1$ donc $ -2\leq 2 \cos n\leq 2$ . (1)
Par ailleurs , on a $(-1)^n=\left\lbrace \begin{array}{l} 1 \text{ si } n \text{ est pair. }\\ -1 \text{ si } n \text{ est impair. }\end{array} \right. $; on a donc pour tout $n \in \mathbb{N}$: $-1\leq (-1)^n\leq 1$ donc $ -3\leq 3 \times(-1)^n\leq 3$ .(2)
En ajoutant (1) et (2) on obtient pour tout $n \in \mathbb{N} : u_n \leq 5 - 3n$
Or, $\lim\limits_{n \to +\infty} (5-3n)=-\infty$, d'où :$ \lim\limits_{n \to +\infty} u_n=-\infty$
Exemple 2 :
Étudier la limite de la suite $\left( u_n \right) $ définie par : $u_n = n^4(\cos n - 2)$
Comme $-1 \leq \cos n \leq 1$, on a : $-3 \leq \cos n - 2\leq -1$
Donc en multipliant par $n^4$ qui est positif, il vient : $u_n \leq -n^4$
Or $\lim\limits_{n \to +\infty} -n^4=-\infty$, d'où :$ \lim\limits_{n \to +\infty} u_n=-\infty$
Exercice :
l'affirmation "une suite qui diverge vers $+\infty$ est nécessairement croissante" est-elle vraie ?
Réponse : non ! Considérer : $u_n = (-1)^ n + n$
On a, pour tout $n \in \mathbb{N}: u_n\geq -1 + n$
Donc, par comparaison : $\left( u_n \right) $ diverge vers $+\infty$
Cependant $\left( u_n \right) $ n'est pas croissante. En effet, pour tout $n \in \mathbb{N}$, on a :
$u_{n+1} - u_n = (-1)^{n+1} + n + 1 - (-1)^n - n = (-1)^{n+1}(1 + 1) + 1 = 2(-1)^{n+1} + 1 =\left\lbrace \begin{array}{l} 3 \text{ si } n \text{ est impair. }\\ -1 \text{ si } n \text{ est pair. }\end{array} \right. $
On a donc prouvé que $u_{n+1} - u_n$est de signe variable.
Donc la suite $\left( u_n \right) $ n'est ni croissante, ni décroissante.
6.2. Théorème d'encadrement ou des "gendarmes"
· À partir d'un certain rang : $u_n\leq v_n \leq w_n$
· $\left( u_n \right) $et $(w_n)$ convergent vers le même réel $l$.
Alors $(v_n)$ converge vers $l$.
Démonstration :
Notons $N_0$ le rang à partir duquel on a : $u_n\leq v_n \leq w_n$
Soit $I$ un intervalle ouvert centre en $l$. Notons $\epsilon$ son rayon. On a donc $I = ]l - \epsilon, l + \epsilon[$.
Comme $\left( u_n \right) $ converge vers $l$, à partir d'un certain rang $N_1$ on a : $u_n \in I$.
Comme $(w_n)$ converge vers $l$, à partir d'un certain rang $N_2$ on a : $w_n \in I$.
Pour $n\geq max(N0, N1, N2)$, comme $u_n \leq v_n\leq w_n$, on a alors :$ v_n \in I$
Bilan : tout intervalle ouvert $I$, centré en $l$, contient tous les termes de la suite $(v_n)$ à partir d'un certain rang (à
savoir $max(N_0, N_1, N_2)$). Donc la suite $(v_n)$ converge bien vers $l$.
Exemple 1 : déterminer la limite de la suite $(v_n)$ définie par :$v_n= \dfrac{3n+5(-1)^n}{2n} $.
Méthode : on encadre $v_n$ .
Pour tout entier $n \in \mathbb{N}+^{\star}$ on a : $-1\leq (-1)^n\leq 1$
Donc en multipliant par $5$ on a $-5\leq 5(-1)^n\leq 5$;
puis en ajoutant $3n$ il vient : $3n-5\leq 3n+5(-1)^n\leq 3n+5$;
enfin en divisant par $2n > 0 $ on obtient : $\dfrac{3n-5}{2n} \leq \dfrac{3n+5(-1)^n}{2n} \leq \dfrac{3n+5}{2n}$
Posons, pour $n \in \mathbb{N}+^{\star}$ :$ u_n =\dfrac{3n-5}{2n}$ et $w_n = \dfrac{3n+5}{2n}$.
On peut écrire $ u_n =\dfrac{3n-5}{2n}=\dfrac{n\left(3-\dfrac{5}{n}\right)}{2n}=\dfrac{\left(3-\dfrac{5}{n}\right)}{2}$ d'où $\lim\limits_{n \to +\infty} u_n=\dfrac{3}{2}$.
De même on a $w_n =\dfrac{3n+5}{2n}==\dfrac{\left(3+\dfrac{5}{n}\right)}{2}$ d'où $\lim\limits_{n \to +\infty} w_n=\dfrac{3}{2}$.
Les suites $\left( u_n \right) $ et $(w_n)$ convergent vers $\dfrac{3}{2}$ . De plus, pour tout $n \in \mathbb{N}+^{\star}: u_n \leq v_n \leq w_n$.
D'après le théorème des gendarmes, on a donc : $\lim\limits_{n \to +\infty} v_n=\dfrac{3}{2}$.
Exemple 2 : déterminer la limite de la suite $\left( u_n \right) $ définie par :$ u_n =\dfrac{\sqrt{n^2+1}}{n}$ pour $n\geq 1$.
On a : $n^2 < n^ 2 + 1$
En outre, $n^ 2 + 1< ( n + 1)^2$ car $2n > 2 > 0$
On a donc l'encadrement suivant : $n^2 < n^2 + 1 < (n + 1)^2$
Par passage à la racine (tous les membres sont positifs), il vient :
$n < n^2 + 1 < n + 1$
Puis en divisant par $n$ (positif) : $1 < u_n < 1 + \dfrac{1}{n}$
Comme $\lim\limits_{n \to +\infty} 1=1$ et $\lim\limits_{n \to +\infty} 1+\dfrac{1}{n}=1$ on en déduit (théorème des gendarmes) que $\lim\limits_{n \to +\infty} u_n=1$
6.3. Corollaire
Soient $\left( u_n \right) $ et $(\epsilon_n)$ deux suites telles que :· Il existe un réel $l $ tel que pour tout $n : |u_n - l| \leq \epsilon_n$
· La suite $(\epsilon_n)$ converge vers 0 : $\lim\limits_{n \to +\infty} \epsilon_n=0$
Alors la suite $\left( u_n \right) $ converge vers $l$.
Démonstration
L'inégalité $|u_n - l|\leq \epsilon_n$ s'écrit encore :$ l - \epsilon_n\leq u_n \leq l+\epsilon_n$
Le théorème des gendarmes permet de conclure.
6.4. Théorème Passage à la limite dans une inégalité
Alors :$ \lim\limits_{n \to +\infty} u_n+\infty)v_n$.
Bien noter que des inégalités strictes deviennent larges par passage à la limite.
Démonstration
Nous aurons besoin du lemme suivant :
Démonstration du lemme :
Notons $l$ la limite de $\left( u_n \right) $. Raisonnons par l'absurde. On suppose que $l < 0$.
Posons $\epsilon = -\frac{l}{2}$.
Comme la suite $\left( u_n \right) $ converge, on aura à partir d'un certain rang : $u_n \in ]l - \epsilon ; l + \epsilon[$
En particulier : $u_n < l + \epsilon \leq l-\frac{l}{2}\leq \frac{l}{2}<0$
Ce qui contredit la positivité de $\left( u_n \right) $. Donc $l\geq 0$ et le lemme est démontré.
On en déduit le théorème en appliquant le lemme à la suite $(v_n - u_n)$.
7. Étude de la convergence des suites géométriques
7.1. Théorème
· Si $a \in ]1 ; +\infty[ $ alors $\left( u_n \right) $ est divergente (vers $+\infty$)
· Si $a = 1$ alors $\left( u_n \right) $ est constante (donc convergente vers 1)
· Si $a \in ]-1 ; 1[$ alors $\left( u_n \right) $ est convergente vers 0
· Si $a \in]-\infty ; -1]$ alors $\left( u_n \right) $ n'a pas de limite.
Démonstration : Nous allons utiliser le résultat suivant :
7.2. Lemme Inégalité de Bernoulli
Remarque : on peut étendre cette inégalité à $x \in ]-1, +\infty[$
Démonstration du lemme :
Soit $x \in \mathbb{R}^+$. On considère la propriété $P(n)$ définie pour tout $n \in \mathbb{N}$par : $P(n) : (1+ x)^n\geq 1 + nx$
· On a $P(0)$ puisque $(1 + x)^ 0\geq 1 + 0x$ pour tout $x \in \mathbb{R} ^ (+)$.
·
Montrons que, pour tout $n \in \mathbb{N}: P(n) \Rightarrow P(n + 1)$
Soit $n \in \mathbb{N}$. Supposons $P(n) : (1+ x)^ n\geq 1 + nx$
Comme $x > 0$, on a aussi $1 + x > 0$. En multipliant l'inégalité ci-dessus par $(1 + x)$, on obtient :
$(1+ x)^{n+1}\geq (1 + nx)(1 + x)$
Or :$ (1 + nx)(1 + x) = 1 + x + nx + n x^2 = 1 + (n + 1)x + n x^2$
Comme $n x^2\geq 0$, on a : $(1 + nx)(1 + x)\geq 1 + (n + 1)x$
D'où : $(1+ x)^{n+1}\geq 1 + (n + 1)x$
Ce qui est $P(n + 1)$.
Bilan : on a $P(0)$ et pour tout $n$ de $\mathbb{N} : P(n) \Rightarrow P(n + 1)$
Donc, pour tout $n$ de $\mathbb{N}$, on a : $P(n): (1+ x)^ n\geq 1 + nx$
Prouvons maintenant le théorème 7.1. :
· Supposons $a \in ]1 ; +\infty[$. Posons $x = a - 1$. Alors $x \in ]0 ; +\infty[$.
D'après l'inégalité de Bernoulli : $a^n = (1+ x)^n\geq 1 + nx$
Or,$ \lim\limits_{n \to+\infty} 1 + nx = +\infty$.
Par comparaison, on en déduit :$ \lim\limits_{n \to +\infty} a^n = +\infty$
La suite $\left( u_n \right) $ diverge donc vers $ +\infty.$
· Si $a = 1$, le résultat est évident.
· Supposons maintenant $a \in ]-1 ; 1[$.
Si $a = 0$, le résultat est évident.
Si $a \neq 0$, posons : $a' = \dfrac{1}{|a|}$
Ainsi : $a' \in ]1 ; +\infty[$
D'après le résultat précédent :$ \lim\limits_{n \to +\infty} (a')^n=+\infty$
Par passage à l'inverse, nous obtenons : $\lim\limits_{n \to +\infty} |a|^n= 0$
D'où : $\lim\limits_{n \to +\infty} a^n = 0$
La suite $\left( u_n \right) $ converge donc vers 0.
· Supposons $a \in]-\infty ; -1]$.
Raisonnons par l'absurde : supposons que la suite $(a_ n)$ converge vers un certain entier $l$.
Soit $I = ]\frac{l}{2};\frac{3l}{2}[$ est un intervalle ouvert centré en $l$. D'après notre hypothèse, il existe un rang $N$ à partir duquel, on aura : $a_n \in I$
Autrement dit :$ l/2< a_n < 0,$ d'où : $0 < (3l/2)$
Et si $n$ est impair alors $a_n < 0$ d'où :$l/2<0$
soit $ l < 0$
D'où une contradiction. Donc la suite $(a_n)$ diverge.
Exemple 1:·
Étudier la limite de la suite $\left( u_n \right) $ définie par :$ u_n = (2 + n)^n$
On sait que pour tout $n \in \mathbb{N}, on a : (2 + n)^ n\geq 2^ n$.
Or,$ \lim\limits_{n \to +\infty} 2^n=+\infty$(théorème 7.1.), donc la suite $\left( u_n \right) $ diverge vers $+\infty$.
Exemple 2 :
Soit $\left( u_n \right) $ la suite définie pour $n \in \mathbb{N}$ par :$ u_n = 1 + \dfrac{1}{3} + \left(\dfrac{1}{3}\right )^2 + \ldots+ \left(\dfrac{1}{3}\right )^n
=\displaystyle\sum_{k=0}^n\left(\dfrac{1}{3}\right )^k$
Chaque terme de la suite $\left( u_n \right) $ est la somme des $(n + 1)$ termes d'une suite géométrique de raison $q = \dfrac{l}{3} $ et de premier terme $P = 1$. On a donc :
$u_n =\dfrac{1- \text {raison } ^{ \text { Nombre de termes } } }{1- \text {raison }}\times \text { Premier terme }$
On obtient donc
$u_n=\dfrac{1-\left (\dfrac{1}{3}\right)^{n+1}}{1-\dfrac{1}{3}} \times 1= \dfrac{3}{2}\times \left (1-\left (\dfrac{1}{3}\right)^{n+1}\right )$
Or $\lim\limits_{n \to +\infty}\left( \dfrac{1}{3}\right) ^n= 0$ (théorème 7.1.) donc : $\lim\limits_{n \to +\infty} u_n=\dfrac{3}{2}$.
Soit $e$ le nombre vu dans l'application 6.7 et $\left( u_n \right) $ la suite définie pour $n\geq 1$ par $u_n = \displaystyle\sum_{k=1}^n e^{-k}$
On a :$ \displaystyle\sum_{k=1}^n e^{-k}=\dfrac{1-\left (\dfrac{1}{e}\right)^{n}}{1-\dfrac{1}{e}}= \dfrac{1-\left (\dfrac{1}{e}\right)^{n}}{e-1}$ Mais comme $0 < \dfrac{1}{e}< 1$ on déduit $\lim\limits_{n \to +\infty} \left (\dfrac{1}{e}\right)^{n}=0$ (théorème 7.1.) . On peut donc conclure $\lim\limits_{n \to +\infty} \displaystyle\sum_{k=1}^n e^{-k}=\dfrac{1}{e-1}$
7.3. Généralisation : limite de la somme des termes d'une suite géométrique :
Pour le démontrer, il suffit d'écrire que : $sum_(k=0)^n q^k=(1-q ^ (n+1))/(1-q)$
puis d'utiliser le théorème 7.1.
Exercice : démontrer que pour tout entier naturel $a$ non nul et tout réel $x$ de $[0 ; 1[$ :
$\lim\limits_{n \to +\infty} \displaystyle\sum_{p=0} ^ n ( - x^a)^ p=\dfrac{1}{1+x^a}$
Solution : on a une somme de termes consécutifs d'une suite géométrique de raison $- x^a$:
Donc $ \displaystyle\sum_{p=0} ^ n ( - x^a)^ p= \dfrac{1-(-x^a)^{n+1}}{1-(-x^a)}=\dfrac{1--(-x^a)^{n+1}}{1+x^a} $
Or $-x^a \in ]-1 ; 1[$ donc :$\lim\limits_{n \to +\infty}( - x^a)^(n+1)=0$ puis on a :$\lim\limits_{n \to +\infty}\displaystyle\sum_{p=0}^ n ( - x^a)^ p=\dfrac{1}{1+x^a}$
8. Étude des suites arithmético-géométriques (ou récurrentes linéaires d'ordre 1)
Il s'agit des suites récurrentes définies par : $\left\lbrace \begin{array}{l} u_0 \\ u_{n+1}=a u_n + b\end{array} \right. $ où $a, b \in \mathbb{R}$.
On constate que si $b = 0$, la suite $\left( u_n \right) $ est géométrique de raison $a$ ;
si $a = 1$, la suite $\left( u_n \right) $ est arithmétique de raison $b$.
Et si $a = 0$, la suite $\left( u_n \right) $ est stationnaire (à partir du rang 1) égale à $b$.
Dans la suite, on suppose $a\neq 1$.
L'objectif est de déterminer une formule explicite (expression de un en fonction de $n$) afin, notamment,
d'étudier le comportement asymptotique de la suite $\left( u_n \right) $.
L'idée de la démarche qui suit est la suivante : si $\left( u_n \right) $ et $(w_n)$ sont deux suites qui vérifient $u_{n+1} = au_n + b$ et $ w_{n+1} = aw_n + b$ alors leur différence $v_n$ est une suite géométrique de raison $a$.
En effet, pour tout $n$, on a :$ v_{n+1} = u_{n+1} - w_{n+1} = a_un + b - aw_n - b = a(u_n - w_n) = av_n$
Il suffit donc de chercher une suite $(w_n)$ la plus simple possible vérifiant la relation $w_(n+1 )= aw_n + b$. Inutile de chercher bien loin : supposons $(w_n)$ constante. Notons $\beta$
cette constante. On a alors :$a=a \beta +b$.
Comme $a \neq 1$, il vient : $\beta= \dfrac{b}{1-a}$
En conséquence, la suite $(v_n)$ définie par $v_n = u_n - \beta$, où $\beta= \dfrac{b}{1-a}$, est géométrique de raison $a$.
On en déduit que pour tout $n : v_n = v_0 a^n = (u_0 - \beta)a^ n$
D'où : $u_n = (u_0 - \beta)a^n + a$
Comme, on connaît le comportement asymptotique des suites géométriques $(a^n)$, on en déduit celui de $\left( u_n \right) $ :
· Si $u_0 = a$ alors $\left( u_n \right) $ est constante égale à $a$.
· Si ($a \in ]-1 ; 1[$ et $u_0 \neq \beta$ ), alors $\left( u_n \right) $ converge vers $\beta$.
· Si ($a > 1 $ et $u_0\neq \beta$), alors $\left( u_n \right) $ diverge vers $+\infty$ (si $u_0 > \beta $) ou $-\infty$ (si $u_0 < \beta$).
· Si ($a \leq -1$ et $u_0\neq \beta$), alors $\left( u_n \right) $ diverge.
Exemple de mise en oeuvre :
On considère la suite $\left( u_n \right) $ définie par :
$\left\lbrace \begin{array}{l} u_0= 5\\ u_{n+1}=2u_n-3\end{array} \right. $
Exprimer $u_n$ en fonction de $n$.
On cherche $\beta$ tel que : $\beta = 2 \beta - 3$, donc $\beta=3$.
On peut donc écrire : $\left\lbrace \begin{array}{l} u_{n+1}=2u_n-3\\ \beta = 2 \beta - 3\end{array} \right. $
En retranchant membre à membre : $u_{n+1} - \beta = 2\left(u_n - \beta\right)$
La suite $(v_n)$ définie par $v_n = u_n - \beta$ est donc géométrique de raison $q = 2$ ; son terme initial est $v_0 = u_0 - \beta = 2$.
On a donc, pour tout entier $n : v_n = q^nv_0 = 2^{n+1}$.
Et finalement : $u_n = v_n + \alpha = 2^{n+1} + 3$.
(On pouvait aussi démontrer ce résultat par récurrence après l'avoir conjecturé) .
- Vues: 33481