Baccalauréat S Nouvelle-Calédonie Mars 2017 - Correction Exercice 3
Correction de l'exercice 3 (4 points)
Les trois parties de cet exercice sont indépendantes. Des étudiants d'une université se préparent à passer un examen pour lequel quatre thèmes (A, B, C et D) sont au programme.
Partie A
Sur les 34 sujets de l'examen déjà posés, 22 portaient sur le thème A. Peut-on rejeter au seuil de $95\,\%$ l'affirmation suivante : « il y a une chance sur deux que le thème A soit évalué le jour de l'examen » ?
On a $n=34\geq 30$, $p=0,5$ donc $np=17\geq 5$ et $n(1-p)=17\geq 5$.
Un intervalle de fluctuation asymptotique de la fréquence du thème A à l’examen est donc
$\begin{align*} I_{34}&=\left[0,5-1,96\sqrt{\dfrac{0,5 \times 0,5}{34}};0,5-1,96\sqrt{\dfrac{0,5 \times 0,5}{34}}\right] \\
&\approx [0,331;0,669]
\end{align*}$
La fréquence observée est $f=\dfrac{22}{34}\approx 0,647 \in I_{34}$.
On ne peut donc pas rejeter, au seuil de $95\%$ l’affirmation faite.
$\quad$
Partie B
Le thème A reste pour beaucoup d'étudiants une partie du programme difficile à maîtriser. Un stage de préparation est alors proposé pour travailler ce thème. Lors de l'examen, on a constaté que s'il y a un exercice portant sur le thème A:
- $30\,\%$ des étudiants n'ayant pas sµivi le stage ne traitent pas l'exercice ;
- $\dfrac{5}{6}$ des étudiants ayant suivi le stage l'ont traité.
On sait de plus que $20\,\%$ des étudiants participent au stage. Lors des résultats de l'examen, un étudiant s'exclame : « Je n'ai pas du tout traité le thème A ». Quelle est la probabilité que cet étudiant ait suivi le stage ? On arrondira le résultat à $0,001$ près.
On appelle $S$ l’événement “l’étudiant a suivi le stage” et $A$ l’événement “l’élève a traité le thème A”. On obtient ainsi l’arbre pondéré suivant :
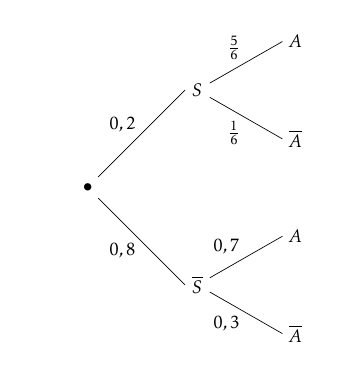
On veut calculer $p_{\overline{A}}(S)$
D’après la formule des probabilités totales on a :
$\begin{align*} p\left(\overline{A}\right)&=p\left(S\cap \overline{A}\right)+p\left(\overline{S}\cap \overline{A}\right) \\
&=0,2\times \dfrac{1}{6}+0,8\times 0,3 \\
&=\dfrac{41}{150}
\end{align*}$
Par conséquent :
$\begin{align*} p_{\overline{A}}(S)&=\dfrac{p\left(\overline{A}\cap S\right)}{p\left(\overline{A}\right)} \\
&=\dfrac{0,2 \times \dfrac{1}{6}}{\dfrac{41}{150}} \\
&=\dfrac{5}{41} \\
&\approx 0,122
\end{align*}$
$\quad$
Partie C
On suppose que la variable aléatoire $T$, associant la durée (exprimée en minutes) que consacre un étudiant de cette université pour la composition de cet examen, suit la loi normale d'espérance $\mu = 225$ et d'écart-type $\sigma$ où $\sigma > 0$. La probabilité qu'un étudiant finisse son examen en moins de $235$~minutes est de $0,98$. Déterminer une valeur approchée de $\sigma$ à $0,1$ près. On pourra, par exemple, introduire la variable aléatoire $ Z = \frac{T - 225}{\sigma}$.
On a :
$\begin{align*} P(T\leq 235) = 0,98 &\iff P(T-225 \leq 235 -225) = 0,98 \\
&\iff P(T-225 \leq 10)=0,98 \\
&\iff P\left(\dfrac{T-225}{\sigma}\leq \dfrac{10}{\sigma}\right)=0,98
\end{align*}$
La variable aléatoire $Z=\dfrac{T-225}{\sigma}$ suit la loi normale centrée réduite.
Or, d’après la calculatrice, $P(Z\leq k)=0,98$ si $ k\approx 2,05$
Par conséquent $\dfrac{10}{\sigma} \approx 2,05$ soit $\sigma \approx 4,9$.
$\quad$
- Vues: 14636
