Baccalauréat S Liban 31 mai 2016

Exercice 1 4 points

Commun à tous les candidats

On considère un solide ADECBF constitué de deux pyramides identiques ayant pour base commune le carré ABCD de centre I.
Une représentation en perspective de ce solide est donnée  en annexe (à rendre avec la copie) .
Toutes les arêtes sont de longueur $1$. L'espace est rapporté au repère orthonormé $\left(\text{A};\vec{\text{AB}},\vec{\text{AD}},\vec{\text{AK}}\right)$.

1. 1. Montrer que IE $= \dfrac{\sqrt{2}}{2}$. En déduire les coordonnées des points I, E et F.
   2. Montrer que le vecteur $\vec{n}\begin{pmatrix}0\\- 2\\\sqrt{2}\end{pmatrix}$ est normal au plan (ABE).
   3. Déterminer une équation cartésienne du plan (ABE).
2. On nomme M le milieu du segment [DF] et N celui du segment [AB].
   1. Démontrer que les plans (FDC) et (ABE) sont parallèles.
   2. Déterminer l'intersection des plans (EMN) et (FDC).
   3. Construire sur l' annexe (à rendre avec la copie)  la section du solide ADECBF par le plan (EMN).
      
      Annexe de l'exercice 1 ( A rendre avec la copie)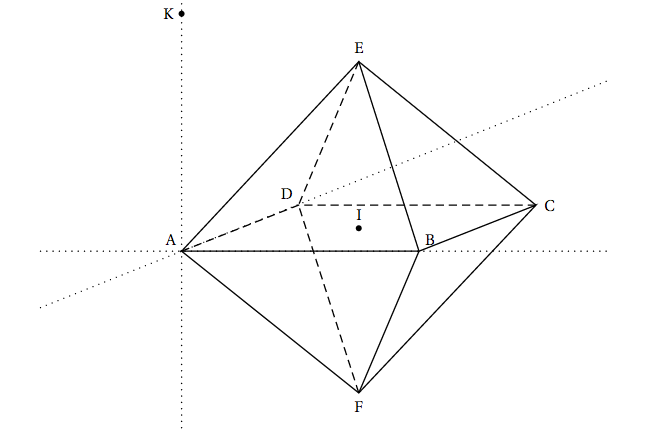
      

Correction de l'exercice 1 (4 points)

Commun à tous les candidats

On considère un solide ADECBF constitué de deux pyramides identiques ayant pour base commune le carré ABCD de centre I.
Une représentation en perspective de ce solide est donnée  en annexe (à rendre avec la copie) .
Toutes les arêtes sont de longueur $1$. L'espace est rapporté au repère orthonormé $\left(\text{A};\vec{\text{AB}},\vec{\text{AD}},\vec{\text{AK}}\right)$.

1. 1. Montrer que IE $= \dfrac{\sqrt{2}}{2}$. En déduire les coordonnées des points I, E et F.
   Dans le triangle $ABC$ rectangle en $B$ on applique le théorème de Pythagore.
   $AC^2=AB^2+BC^2 = 2$ donc $AC= \sqrt{2}$
   $ABCD$ est un carré donc ses diagonales se coupent perpendiculairement en leur milieu.
   Ainsi : $IC=\dfrac{AC}{2}=\dfrac{\sqrt{2}}{2}$.
   Dans le triangle $IEC$ rectangle en $I$ on applique le théorème de Pythagore.
   Par conséquent $IE^2+IC^2=EC^2$
   Donc $IE^2+\dfrac{2}{4}=1$ soit $IE^2=\dfrac{1}{2}$.
   Et $IE=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}$.
   $\quad$
   $\vec{AI}=\dfrac{1}{2}\left(\vec{AB}+\vec{AC}\right)$.
   Donc les coordonnées de $I$ sont $(0,5;0,5;0)$.
   Et $E$ a pour coordonnées $\left(0,5;0,5;\dfrac{\sqrt{2}}{2}\right)$.
   On en déduit donc que les coordonnées de $F$ sont $\left(0,5;0,5;-\dfrac{\sqrt{2}}{2}\right)$.
   $\quad$
   
   2. Montrer que le vecteur $\vec{n}\begin{pmatrix}0\\- 2\\\sqrt{2}\end{pmatrix}$ est normal au plan (ABE).
   On a $\vec{AB}(1;0;0)$ et $\vec{AE}\left(0,5;0,5;\dfrac{\sqrt{2}}{2}\right)$.
   Par conséquent $\vec{n}.\vec{AB}=0+0+0=0$
   Et $\vec{n}.\vec{AE}=-2\times 0,5+\dfrac{2}{2}=-1+1=0$.
   Les deux vecteurs $\vec{AB}$ et $\vec{AE}$ ne sont clairement pas colinéaires.
   Ainsi le vecteur $\vec{n}$ est orthogonal a deux vecteurs non colinéaires du plan $(ABE)$. Il est donc normal à ce plan.
   $\quad$
   
   3. Déterminer une équation cartésienne du plan (ABE).
   Une équation cartésienne de $(ABE)$ est donc de la forme :
   $-2y+\sqrt{2}z+d=0$.
   Le point $A(0;0;0)$ appartient à ce plan donc $0+d=0$ et $d=0$.
   Une équation cartésienne de $(ABE)$ est alors $-2y+\sqrt{2}z=0$.
   $\quad$
2. On nomme M le milieu du segment [DF] et N celui du segment [AB].
   1. Démontrer que les plans (FDC) et (ABE) sont parallèles.
      • Méthode 1 : $ABCD$ est un carré donc $\vec{AB} = \vec{DC}$.
        $\vec{AE}\left(0,5;0,5;\dfrac{\sqrt{2}}{2}\right)$ et $\vec{FC}\left(0,5;0,5;\dfrac{\sqrt{2}}{2}\right)$. Donc $\vec{AE}=\vec{FC}$
        Par conséquent deux vecteurs non colinéaires du plan $(FDC)$ sont colinéaires à deux vecteurs du plan $(ABE)$.
        Les deux plans sont donc parallèles.
      • Méthode 2 : On prouve que le vecteur $\vec{n}$ est orthogonal a deux vecteurs non colinéaires du plan $(FDC)$
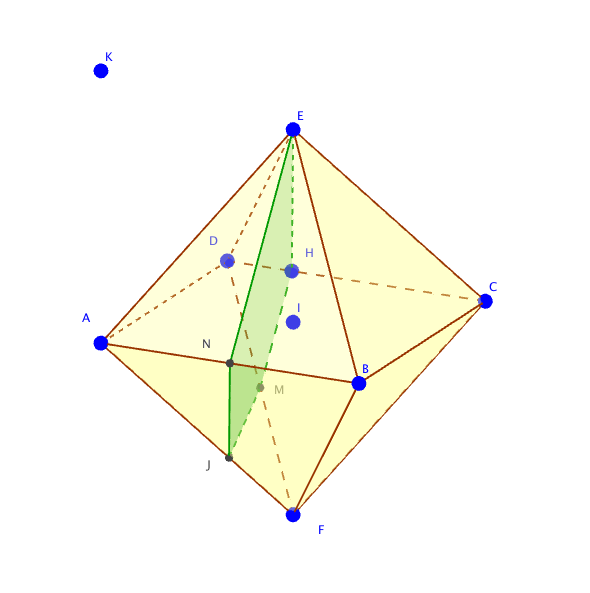
3. Déterminer l'intersection des plans (EMN) et (FDC).
Le point $M$ appartient au plan $(EMN)$ et à $[DF]$.
Il appartient donc à l’intersection des plans $(EMN)$ et $(FDC)$.
On appelle $H$ le point de coordonnées $(0,25;1;0)$.
Il appartient à $[DC]$.
$M$ est le milieu de $[DF]$ donc ses coordonnées sont $\left(0,25;0,75;\dfrac{\sqrt{2}}{4}\right)$.
Ainsi $\vec{MH}\left(0;0,25;-\dfrac{\sqrt{2}}{4}\right)$.
On a également $N(0,5;0;0)$
Donc $\vec{NE}\left(0;0,5;-\dfrac{\sqrt{2}}{2}\right)$.
Ainsi $\vec{NE}=2\vec{MH}$.
Puisque $N$, $M$ et $E$ appartiennent au plan $(EMN)$ $H$ aussi.
$H$ appartient donc également à l’intersection des plans $(EMN)$ et $(FDC)$.
L’intersection de ces deux plans est par conséquent la droite $(MH)$.
$\quad$
Autre solution pour déterminer graphiquement H :
Les plans $(FDC)$ et $(ABE)$ sont parallèles. Par conséquent les intersections du plan $(EMN)$ avec ces deux plans sont parallèles.
$(EN)$ est l’intersection de $(EMN)$ et de $(AEB)$.
On trace donc la parallèle à $(EN)$ passant par $M$. Elle coupe $(DC)$ en $H$.

4. Construire sur l' annexe (à rendre avec la copie)  la section du solide ADECBF par le plan (EMN).
   
   Annexe de l'exercice 1 ( A rendre avec la copie)

Les points $E$, $N$, $M$ et $H$ appartiennent à cette section.
On construit le point $J$ comme intersection entre la droite parallèle à $(EH)$ passant par $N$ et le segment $[AF]$ puisque les plans $(EDC)$ et $(ABF)$ sont parallèles (mêmes argument que pour la question 2.a.

Exercice 2 4 points

Commun à tous les candidats

Sur un court de tennis, un lance-balle permet à un joueur de s'entraîner seul. Cet appareil envoie des balles une par une à une cadence régulière. Le joueur frappe alors la balle puis la balle suivante arrive. Suivant le manuel du constructeur, le lance-balle envoie au hasard la balle à droite ou à gauche avec la même probabilité.
Dans tout l'exercice, on arrondira les résultats à $10^{-3}$ près.

Partie A

Le joueur s'apprête à recevoir une série de 20 balles.

1. Quelle est la probabilité que le lance-balle envoie 10 balles à droite ?
2. Quelle est la probabilité que le lance-balle envoie entre 5 et 10 balles à droite ?

Partie B

Le lance-balle est équipé d'un réservoir pouvant contenir 100 balles. Sur une séquence de 100 lancers, 42 balles ont été lancées à droite. Le joueur doute alors du bon fonctionnement de l'appareil. Ses doutes sont-ils justifiés ?

Partie C

Pour augmenter la difficulté le joueur paramètre le lance-balle de façon à donner un effet aux balles lancées. Elles peuvent être soit « liftées » soit « coupées ». La probabilité que le lance-balle envoie une balle à droite est toujours égale à la probabilité que le lance-balle envoie une balle à gauche. Les réglages de l'appareil permettent d'affirmer que :

• la probabilité que le lance-balle envoie une balle liftée à droite est $0,24$ ;
• la probabilité que le lance-balle envoie une balle coupée à gauche est $0,235$.

Si le lance-balle envoie une balle coupée, quelle est la probabilité qu'elle soit envoyée à droite ?

Correction de l'exercice 2 (5 points)

Commun à tous les candidats

Sur un court de tennis, un lance-balle permet à un joueur de s'entraîner seul. Cet appareil envoie des balles une par une à une cadence régulière. Le joueur frappe alors la balle puis la balle suivante arrive. Suivant le manuel du constructeur, le lance-balle envoie au hasard la balle à droite ou à gauche avec la même probabilité.
Dans tout l'exercice, on arrondira les résultats à $10^{-3}$ près.

Partie A

Le joueur s'apprête à recevoir une série de 20 balles.

1. Quelle est la probabilité que le lance-balle envoie 10 balles à droite ?

On répète $\1$  fois, de façon indépendante, l’expérience «\2 » qui comporte 2 issues :

• « \3 » considéré comme succès, de probabilité $p=\4$
• « \5 » considéré comme échec, de probabilité $q=1-p=\6$

Nous sommes donc en présence d’un schéma de Bernoulli et la variable aléatoire $\7$ prenant pour valeurs le nombre de succès obtenus suit la loi binomiale de paramètres $\1$  et $\4$ notée $\mathscr{B}(\1;\4)$ .

Pour tout entier $k$ où $0\leq k\leq \1$, on a $$P(\7=k)=\binom{\1}{k}\times \left(\4\right)^k\times\left( \6\right)^{\1-k}$$


On veut calculer $P(X=10)=\displaystyle \binom{20}{10}\times 0,5^{10}\times 0,5^{20-10}\approx 0,176$.


2ND DISTR 0binomFdP( \1 , \2,\3)EXE
Avec une calculatrice de type TI $binomFdP(\1,\2,\3) \approx \4$

$$P( \5 = \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
2. Quelle est la probabilité que le lance-balle envoie entre 5 et 10 balles à droite ?
Méthode 1 : On veut calculer $P(5 \leqslant X \leqslant 10)=P(X \leqslant 10)-P(X \leqslant 4) \approx 0,582$.
Méthode 2 :

2ND DISTR AbinomFRép( \1 , \2,\5) -2ND DISTR A binomFRép( \1 , \2,\3)EXE


Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\5)-binomFR\text{é}p(\1,\2,\3) \approx \6$$

$$P( \4 \leq \7\leq\5 )\approx \6 \text{ à } 10^{-\8} \text{ près.}$$

En vidéo !

En vidéo !

Partie B

La proportion $p$ est égale à  $\1$. La taille  $n$  de l'échantillon considéré est égale à  $\2.$
Comme  $ n =\2$ ,   $n \times p  $=\3  et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.

L'intervalle de fluctuation asymptotique au seuil de  $95\% $  est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$ 

$\begin{align*} I_{100} &=\left[0,5-1,96\times \dfrac{\sqrt{0,5\times 0,5}}{\sqrt{100}};0,5-1,96\times \dfrac{\sqrt{0,5\times 0,5}}{\sqrt{100}}\right] \\\\
&=[0,402;0,598]
\end{align*}$
La fréquence observée est $f=0,42 \in I_{100}$.
Au risque d’erreur de $5\%$ l’appareil fonctionne correctement.

Partie C

On appelle $D$ l’événement « la balle est envoyée à droite » et $L$ l’événement « la balle est liftée ».

On a ainsi $p(D\cap L)=0,24$ et $p\left(\overline{D}\cap \overline{L}\right)=0,235$

Ainsi $p_D(L)=\dfrac{p(D \cap L)}{p(D)}=\dfrac{0,24}{0,5}=0,48$.
Par conséquent $p_D\left(\overline{L}\right)=0,52$.
Donc $p\left(D\cap \overline{L}\right)=0,5 \times 0,52 = 0,26$.

D’après la formule des probabilités totales on a :
$$\begin{align*} p\left(\overline{L}\right)&=p\left(D\cap \overline{L}\right)+p\left(\overline{D}\cap \overline{L}\right) \\
&=0,26+0,235 \\
&=0,495
\end{align*}$$

Ainsi $p_{\overline{L}}(D) = \dfrac{p\left(D\cap \overline{L}\right)}{p\left(\overline{L}\right)}=\dfrac{0,26}{0,495}\approx 0,525$.

$\quad$

Exercice 3 4 points

Fonctions et calcul intégral

On considère la fonction $f$ définie sur l'intervalle [0 ; 1] par : \[f(x) = \dfrac{1}{1 + \text{e}^{1 - x}}.\]

Partie A

1. Étudier le sens de variation de la fonction $f$ sur l'intervalle [0 ; 1].
2. Démontrer que pour tout réel $x$ de l'intervalle [0;1], $f(x) = \dfrac{\text{e}^x}{\text{e}^x + \text{e}}$ (on rappelle que $\text{e} = \text{e}^1$).
3. Montrer alors que $\displaystyle\int_0^1 f(x)\:\text{d}x = \ln (2) + 1 - \ln (1 + \text{e})$.

Partie B

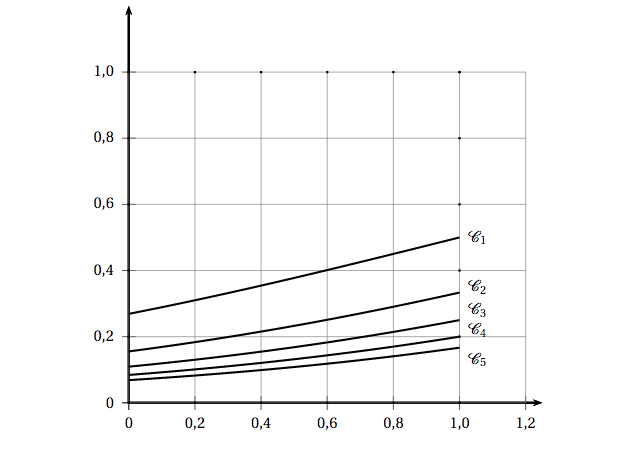
Soit $n$ un entier naturel. On considère les fonctions $f_n$ définies sur [0;1] par: \[f_n(x) = \dfrac{1}{1 + n\text{e}^{1 - x}}.\] On note $\mathcal{C}_n$ la courbe représentative de la fonction $f_n$ dans le plan muni d'un repère orthonormé. On considère la suite de terme général \[u_n = \displaystyle\int_0^1 f_n(x)\:\text{d}x.\]

1. On a tracé en annexe les courbes représentatives des fonctions $f_n$ pour $n$ variant de 1 à 5. Compléter le graphique en traçant la courbe $\mathcal{C}_0$ représentative de la fonction $f_0$.
2. Soit $n$ un entier naturel, interpréter graphiquement $u_n$ et préciser la valeur de $u_0$.
3. Quelle conjecture peut-on émettre quant au sens de variation de la suite $\left(u_n\right)$ ? Démontrer cette conjecture.
4. La suite $\left(u_n\right)$ admet-elle une limite ?

Correction de l'exercice 3 (4 points)

Commun à tous les candidats

Fonctions et calcul intégral

On considère la fonction $f$ définie sur l'intervalle [0 ; 1] par : \[f(x) = \dfrac{1}{1 + \text{e}^{1 - x}}.\]

Partie A

1. Étudier le sens de variation de la fonction $f$ sur l'intervalle [0 ; 1].
$f$ est un quotient de fonctions dérivables sur $[0;1]$ dont le dénominateur ne s’annule pas (puisque la fonction exponentielle est strictement positive). Elle est donc également dérivable sur cet intervalle.
Ainsi $f'(x)=-\dfrac{-\text{e}^{1-x}}{\left(1+\text{e}^{1-x}\right)^2}$ $= \dfrac{\text{e}^{1-x}}{\left(1+\text{e}^{1-x}\right)^2}$.
La fonction exponentielle étant positive, pour tout réel $x\in[0;1]$ on a donc $f'(x) > 0$.
La fonction $f$ est donc croissante sur $[0;1]$.

2. Démontrer que pour tout réel $x$ de l'intervalle [0;1], $f(x) = \dfrac{\text{e}^x}{\text{e}^x + \text{e}}$ (on rappelle que $\text{e} = \text{e}^1$).
$\begin{align*} f(x)&=\dfrac{1}{1+\text{e}^{1-x}} \\
&=\dfrac{1}{1+\text{e}^{1-x}} \times \dfrac{e^x}{e^x}\\
&=\dfrac{\text{e}^x}{\text{e}^x+\text{e}}
\end{align*}$

3. Montrer alors que $\displaystyle\int_0^1 f(x)\:\text{d}x = \ln (2) + 1 - \ln (1 + \text{e})$.
On a ainsi :
$$\begin{align*} \int_0^1f(x)\mathrm{d}x &= \Big[\ln\left(\text{e}^x+\text{e}e\right)\Big]_0^1 \\
&= \ln(2\text{e})-\ln(1+\text{e}) \\
&=\ln(2)+\ln(\text{e})-\ln(1+\text{e})\\
&=\ln(2)+1-\ln(1+\e)
\end{align*}$$

Partie B

Soit $n$ un entier naturel. On considère les fonctions $f_n$ définies sur [0;1] par: \[f_n(x) = \dfrac{1}{1 + n\text{e}^{1 - x}}.\] On note $\mathcal{C}_n$ la courbe représentative de la fonction $f_n$ dans le plan muni d'un repère orthonormé. On considère la suite de terme général \[u_n = \displaystyle\int_0^1 f_n(x)\:\text{d}x.\]

1. On a tracé en annexe les courbes représentatives des fonctions $f_n$ pour $n$ variant de 1 à 5. Compléter le graphique en traçant la courbe $\mathcal{C}_0$ représentative de la fonction $f_0$.
$f_0(x)=1$ pour tout $x\in[0;1]$.

2. Soit $n$ un entier naturel, interpréter graphiquement $u_n$ et préciser la valeur de $u_0$.
$u_n$ correspond à l’aire du domaine compris entre la courbe $\mathscr{C}_n$, l’axe des abscisses et les droites d’équation $x=0$ et $x=1$.
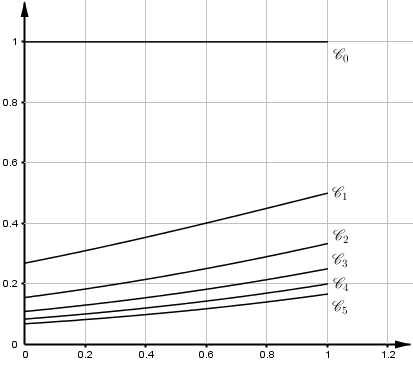
Puisque la fonction $f_0$ est constante sur $[0;1]$ alors $u_0=1\times 1=1$.

3. Quelle conjecture peut-on émettre quant au sens de variation de la suite $\left(u_n\right)$ ? Démontrer cette conjecture.
La suite $\left(u_n\right)$ semble être décroissante.
$\quad$
$\begin{align*} u_{n+1}-u_{n} &=\displaystyle \int_0^1 \dfrac{1}{1+(n+1)\text{e}^{1-x}}\mathrm{d}x-\int_0^1 \dfrac{1}{1+n\text{e}^{1-x}}\mathrm{d}x \\
&= \int_0^1 \left(\dfrac{1}{1+(n+1)\text{e}^{1-x}}-\dfrac{1}{1+n\text{e}^{1-x}}\right) \mathrm{d}x \\
&= \int_0^1 \dfrac{1+ne^{1-x}-1-(n+1)\text{e}^{1-x}}{\left(1+(n+1)\text{e}^{1-x}\right)\left(1+n\text{e}^{1-x}\right)} \mathrm{d}x\\
&=\int_0^1 \dfrac{-\text{e}^{1-x}}{\left(1+(n+1)\text{e}^{1-x}\right)\left(1+n\text{e}^{1-x}\right)} \mathrm{d}x
\end{align*}$
Du fait de la positivité de l’exponentielle, $u_{n+1}-u_{n}<0$ et la suite est bien décroissante.

4. La suite $\left(u_n\right)$ admet-elle une limite ?
Pour tout $n$ on a $u_n > 0$ comme intégrale d’une fonction continue strictement positive sur $[0;1]$.
La suite $\left(u_n\right)$ est donc décroissante et minorée par $0$. Elle est par conséquent convergente et possède ainsi une limite.

Exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse en justifiant la réponse.
Un point est attribué par réponse exacte justifiée. Une réponse non justifiée ne sera pas prise en compte et l'absence de réponse n'est pas pénalisée.

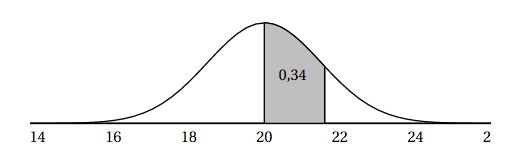
• Sur le schéma ci-dessous on a représenté la courbe de densité d'une variable aléatoire $X$ qui suit une loi normale d'espérance $\mu = 20$. La probabilité que la variable aléatoire $X$ soit comprise entre $20$ et $21,6$ est égale à $0,34$.
  
  Affirmation 1 : La probabilité que la variable aléatoire $X$ appartienne à l'intervalle $[23,2; + \infty[$ vaut environ 0,046.
• Soit $z$ un nombre complexe différent de 2. On pose : \[Z = \dfrac{\text{i}z}{z - 2}.\]
  Affirmation 2 : L'ensemble des points du plan complexe d'affixe $z$ tels que $|Z| = 1$ est une droite passant par le point A(1 ;0).
  Affirmation 3 : $Z$ est un imaginaire pur si et seulement si $z$ est réel.
• Soit $f$ la fonction définie sur $\mathbb{R}$ par : \[f(x) = \dfrac{3}{4 + 6\text{e}^{- 2x}}.\]
  Affirmation 4 : L'équation $f(x) = 0,5$ admet une unique solution sur $\mathbb{R}$.
  Affirmation 5 : L' algorithme suivant affiche en sortie la valeur $0,54$.
  $$ \begin{array}{|l|l|} \hline \text{ Variables : } & X \text{ et } Y \text{ sont des réels}\\ \text{Initialisation :}& X \text{ prend la valeur } 0\\ & Y \text{ prend la valeur } \dfrac{3}{10} \\ \text{ Traitement :} &\text{ Tant que } Y < 0.5 \\ &\quad X \text{ prend la valeur } X + 0,01 \\ &\hspace{0.4cm} Y \text{ prend la valeur } \dfrac{3}{4 + 6\text{e}^{- 2X}} \\ &\text{Fin Tant que}\\ \text{Sortie : } & \text{Afficher } X \\ \hline \end{array} $$

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse en justifiant la réponse.
Un point est attribué par réponse exacte justifiée. Une réponse non justifiée ne sera pas prise en compte et l'absence de réponse n'est pas pénalisée.

• Sur le schéma ci-dessous on a représenté la courbe de densité d'une variable aléatoire $X$ qui suit une loi normale d'espérance $\mu = 20$. La probabilité que la variable aléatoire $X$ soit comprise entre $20$ et $21,6$ est égale à $0,34$.
  
• Affirmation 1 : La probabilité que la variable aléatoire $X$ appartienne à l'intervalle $[23,2; + \infty[$ vaut environ 0,046.
Affirmation 1 : fausse
Méthode 1 : On utilise la propriété suivante :

Si $X$ suit la loi normale $\mathcal{N}(\mu;\sigma^2)$ alors $P(\mu-\sigma \leqslant X \leqslant \mu+\sigma)=0,68)$
On a $P(20 \leqslant X \leqslant 21,6) = 0,34$
Donc $P(18,4 \leqslant X \leqslant 21,6) = 0,68$ soit $P(20-1,6 \leqslant X \leqslant 20+1,6)=0,68)$.
Cela signifie donc que $\sigma \approx 1,6$.
Ainsi $P(X \geqslant 23,2) = 0,5-P(20 \leqslant X \leqslant 23,2) \approx 0,023$

 

2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$

$$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
Méthode 2 : $X$ suit la loi normale $\mathcal{N}(20;\sigma^2)$ donc $T=\dfrac{X-20}{\sigma}$ suit $\mathcal{N}(0;1)$
$\begin{align*} P(20 \leqslant X \leqslant 21,6) = 0,34 &\iff P\left(\dfrac{20-20}{\sigma} \leqslant \dfrac{X-20}{\sigma} \leqslant \dfrac{20,6-20}{\sigma}\right) = 0,34\\
& \iff P\left(0 \leqslant T \leqslant \dfrac{1,6}{\sigma}\right) = 0,34 \\
&\iff0,5+P\left( T \leqslant \dfrac{1,6}{\sigma}\right) = 0,84\\
&\iff \pi\left( \dfrac{1,6}{\sigma}\right) = 0,84\\ &\iff \dfrac{1,6}{\sigma}=\pi^{-1}(0,84)\\ &\iff \sigma= \dfrac{1,6}{\pi^{-1}(0,84)}\\ &\text{ donc } \sigma\approx 1,6089
\end{align*}$

2ND DISTR 3Fracnormale( $\1 $ )EXE
Avec une calculatrice de type TI

$$Fracnormale( \1 ) \approx \2$$

$$\pi^{-1}( \1)\approx \2 \text{ à } 10^{-\3} \text{ près.}$$

 

2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$

$$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$

En vidéo !

• Soit $z$ un nombre complexe différent de 2. On pose : \[Z = \dfrac{\text{i}z}{z - 2}.\]
• Affirmation 2 : L'ensemble des points du plan complexe d'affixe $z$ tels que $|Z| = 1$ est une droite passant par le point A(1 ;0).
Affirmation 2 : vraie
$\begin{align*} |Z|=1 &\iff |\text{i} z|=|z-2| \\
&\iff |z|=|z-2|
\end{align*}$
Cet ensemble de points est donc la médiatrice du segment $[BC]$ où $B$ a pour affixe $0$ et $C$ a pour affixe $2$.
Cette médiatrice passe par le milieu de $[BC]$ qui est $A$ d’affixe $1$.

• Affirmation 3 : $Z$ est un imaginaire pur si et seulement si $z$ est réel.
Affirmation 3 : vraie
Pour tout $z\neq 2$,
$\begin{align*} Z&=\dfrac{\text{i} z}{z-2} \\
&=\dfrac{\text{i}(x+\text{i} y)}{x+\text{i} y -2} \\
&=\dfrac{(\text{i} x-y)(x-2-\text{i} y)}{(x-2)^2+y^2} \\
&=\dfrac{(x-2)x\text{i} -y(x-2)+xy+\text{i} y^2}{(x-2)^2+y^2} \\
&\dfrac{2y+\text{i}\left((x-2)x+y^2\right)}{(x-2)^2+y^2}
\end{align*}$
$Z$ est un imaginaire pur si, et seulement si, $2y =0$ soit $y=0$ c’est-à-dire $z$ est un réel.
• Soit $f$ la fonction définie sur $\mathbb{R}$ par : \[f(x) = \dfrac{3}{4 + 6\text{e}^{- 2x}}.\]
• Affirmation 4 : L'équation $f(x) = 0,5$ admet une unique solution sur $\mathbb{R}$.
Affirmation 4 : vraie
$\begin{align*} f(x)=0 &\iff \dfrac{3}{4+6\text{e}^{-2x}}=0,5 \\
&\iff 3=2+3\text{e}^{-2x} \\
&\iff 1=3\text{e}^{-2x} \\
&\iff \dfrac{1}{3} = \text{e}^{-2x} \\
&\iff -\ln 3=-2x \\
&\iff x = \dfrac{\ln 3}{2}
\end{align*}$
• Affirmation 5 : L' algorithme suivant affiche en sortie la valeur $0,54$.
  $$ \begin{array}{|l|l|} \hline \text{ Variables : } & X \text{ et } Y \text{ sont des réels}\\ \text{Initialisation :}& X \text{ prend la valeur } 0\\ & Y \text{ prend la valeur } \dfrac{3}{10} \\ \text{ Traitement :} &\text{ Tant que } Y < 0.5 \\ &\quad X \text{ prend la valeur } X + 0,01 \\ &\hspace{0.4cm} Y \text{ prend la valeur } \dfrac{3}{4 + 6\text{e}^{- 2X}} \\ &\text{Fin Tant que}\\ \text{Sortie : } & \text{Afficher } X \\ \hline \end{array} $$
Affirmation 5 : fausse
$f(0,54) \approx 0,496~9$ et $f(0,55) \approx 0,500~2$.
L’algorithme va afficher $0,55$.

Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse en justifiant la réponse. Un point est attribué par réponse exacte justifiée. Une réponse non justifiée ne sera pas prise en compte et l'absence de réponse n'est pas pénalisée.

• On considère le système $\left\{\begin{array}{l c l} n &\equiv & 1 \quad [5]\\ n &\equiv & 3 \quad[4] \end{array}\right.$ d'inconnue $n$ entier relatif.
  Affirmation 1 : Si $n$ est solution de ce système alors $n - 11$ est divisible par 4 et par 5.
  Affirmation 2 : Pour tout entier relatif $k$, l'entier $11 + 20k$ est solution du système.
  Affirmation 3 : Si un entier relatif $n$ est solution du système alors il existe un entier relatif $k$ tel que $n = 11 + 20k$.
• Un automate peut se trouver dans deux états A ou B. À chaque seconde il peut soit rester dans l'état où il se trouve, soit en changer, avec des probabilités données par le graphe probabiliste ci-dessous.
  
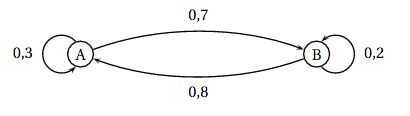
  Pour tout entier naturel $n$, on note $a_n$ la probabilité que l'automate se trouve dans l'état A après $n$ secondes et $b_n$ la probabilité que l'automate se trouve dans l'état B après $n$ secondes. Au départ, l'automate est dans l'état B.
   On considère l'algorithme suivant :
  $$\begin{array}{ |l|l|} \hline \text{ Variables: } & a \text{ et } b \text{ sont des réels}\\ \text{Initialisation:} & a \text{ prend la valeur } 0\\ & b \text{ prend la valeur } 1\\ \text{Traitement: } &\text{Pour } k \text{ allant de 1 à 10} \\ &\hspace{0.4cm} a \text{ prend la valeur } 0,8a + 0,3b \\ &\hspace{0.4cm} b \text{ prend la valeur } 1 - a \\ &\text{ Fin Pour }\\ \text{Sortie: } &\text{Afficher } a \\ &\text{Afficher } b \\ \hline \end{array} $$
  Affirmation 4 : En sortie, cet algorithme affiche les valeurs de $a_{10}$ et $b_{10}$  .
  Affirmation 5 : Après 4 secondes, l'automate a autant de chances d'être dans l'état A que d'être dans l'état B.

Correction de l'exercice de Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse en justifiant la réponse. Un point est attribué par réponse exacte justifiée. Une réponse non justifiée ne sera pas prise en compte et l'absence de réponse n'est pas pénalisée.

• On considère le système $\left\{\begin{array}{l c l} n &\equiv & 1 \quad [5]\\ n &\equiv & 3 \quad[4] \end{array}\right.$ d'inconnue $n$ entier relatif.
• Affirmation 1 : Si $n$ est solution de ce système alors $n - 11$ est divisible par 4 et par 5.
Affirmation 1 : vraie
Soit $n$ une solution de ce système
Alors $n-11 \equiv 1-11 \quad [5] \iff n-11 \equiv -10 \quad [5] \iff \equiv n-11 \equiv 0 \quad [5]$
$n-11$ est donc divisible par $5$.
Et $n-11 \equiv 3-11 \quad [4] \iff n-11 \equiv -8 \quad [4] \iff n-11 \equiv 0 \quad [4]$.
$n-11$ est donc également divisible par $4$.
• Affirmation 2 : Pour tout entier relatif $k$, l'entier $11 + 20k$ est solution du système.

Affirmation 2 : vraie
Soit $k$ un entier relatif et $n=11+20k$.
$11 \equiv 1 \quad [5]$ donc $n=11+5\times 4k \equiv 1 \quad [5]$.
$11 \equiv 3 \quad [4]$ donc $n=11 +4\times 5k \equiv 3 \quad [4]$.
Ainsi $n$ est bien solution du système.

• Affirmation 3 : Si un entier relatif $n$ est solution du système alors il existe un entier relatif $k$ tel que $n = 11 + 20k$.
Affirmation 3 : vraie
$11$ est une solution évidente du système.
Soit $n$ une autre solution.
Par différence, on obtient : $\begin{cases} n-11 \equiv 0 \quad [5] \\n-11\equiv 0 \quad [4] \end{cases}$
Ainsi $n-11$ est divisible à la fois par $4$ et $5$ qui sont premiers entre eux.
D’après le théorème de Gauss, $20=4\times 5$ divise $n-11$.
Il existe donc un entier relatif $k$ tel que $n-11=20k$ soit $n=11+20k$.
• Un automate peut se trouver dans deux états A ou B. À chaque seconde il peut soit rester dans l'état où il se trouve, soit en changer, avec des probabilités données par le graphe probabiliste ci-dessous.
  
  Pour tout entier naturel $n$, on note $a_n$ la probabilité que l'automate se trouve dans l'état A après $n$ secondes et $b_n$ la probabilité que l'automate se trouve dans l'état B après $n$ secondes. Au départ, l'automate est dans l'état B.
   On considère l'algorithme suivant :
  $$\begin{array}{ |l|l|} \hline \text{ Variables: } & a \text{ et } b \text{ sont des réels}\\ \text{Initialisation:} & a \text{ prend la valeur } 0\\ & b \text{ prend la valeur } 1\\ \text{Traitement: } &\text{Pour } k \text{ allant de 1 à 10} \\ &\hspace{0.4cm} a \text{ prend la valeur } 0,8a + 0,3b \\ &\hspace{0.4cm} b \text{ prend la valeur } 1 - a \\ &\text{ Fin Pour }\\ \text{Sortie: } &\text{Afficher } a \\ &\text{Afficher } b \\ \hline \end{array} $$
• Affirmation 4 : En sortie, cet algorithme affiche les valeurs de $a_{10}$ et $b_{10}$  .
Affirmation 4 : fausse
D’après le graphe probabiliste on peut dire que, pour tout entier naturel $n$ on a $a_{n+1}=0,3a_n+0,8b_n$
Or l’algorithme donne la valeur $0,8a+0,3b$ à $a$.
• Affirmation 5 : Après 4 secondes, l'automate a autant de chances d'être dans l'état A que d'être dans l'état B.
Affirmation 5 : vraie
On calcule les différentes valeurs de $a_n$ et $b_n$:
$\begin{array}{|c|c|c|c|c|c|}
\hline
n&0&1&2&3&4 \\
\hline
a_n&0&0,8&0,4&0,6&0,5 \\
\hline
b_n&1&0,2&0,6&0,4&0,5 \\
\hline
\end{array}$
Il y a donc équiprobabilité d’être dans l’état A que dans l’état B après $4$ secondes

Une autrre façon de le voir !

Exercice 5 3 points

Commun à tous les candidats

On considère la suite $\left(z_n\right)$ de nombres complexes définie pour tout entier naturel $n$ par : \[\left\{\begin{array}{l c l} z_0 & =& 0\\ z_{n+ 1}& =& \dfrac{1}{2} \text{i} \times z_n + 5 \end{array}\right.\] Dans le plan rapporté à un repère orthonormé, on note $M_n$ le point d'affixe $z_n$. On considère le nombre complexe $z_{\text{A}} = 4 + 2\text{i}$ et A le point du plan d'affixe $z_{\text{A}}$.

1. Soit $\left(u_n\right)$ la suite définie pour tout entier naturel $n$ par $u_n = z_n - z_{\text{A}}$ .
   1. Montrer que, pour tout entier naturel $n,\: u_{n+1} = \dfrac{1}{2} \text{i} \times u_n$.
   2. Démontrer que, pour tout entier naturel $n$ : \[u_n = \left(\dfrac{1}{2} \text{i}\right)^n (- 4 - 2\text{i}).\]
2. Démontrer que, pour tout entier naturel $n$, les points A, $M_n$ et $M_{n+4}$ sont alignés.

Correction de l'exercice 5 (3 points)

Commun à tous les candidats

On considère la suite $\left(z_n\right)$ de nombres complexes définie pour tout entier naturel $n$ par : \[\left\{\begin{array}{l c l} z_0 & =& 0\\ z_{n+ 1}& =& \dfrac{1}{2} \text{i} \times z_n + 5 \end{array}\right.\] Dans le plan rapporté à un repère orthonormé, on note $M_n$ le point d'affixe $z_n$. On considère le nombre complexe $z_{\text{A}} = 4 + 2\text{i}$ et A le point du plan d'affixe $z_{\text{A}}$.

1. Soit $\left(u_n\right)$ la suite définie pour tout entier naturel $n$ par $u_n = z_n - z_{\text{A}}$ .
   1. Montrer que, pour tout entier naturel $n,\: u_{n+1} = \dfrac{1}{2} \text{i} \times u_n$.
   Soit $n$ un entier naturel.
   $\begin{align*} u_{n+1}&=z_{n+1}-4-2\text{i} \\
   &=\dfrac{1}{2}\text{i} \times z_n+5-4-2\text{i} \\
   &=\dfrac{1}{2}\text{i} \times \left(u_n+4+2\text{i}\right)+1-2\text{i} \\
   &=\dfrac{1}{2}\text{i} \times u_n +2\text{i}-1+1-2\text{i} \\
   &=\dfrac{1}{2}\text{i} \times u_n
   \end{align*}$
   $\quad$
   
   2. Démontrer que, pour tout entier naturel $n$ : \[u_n = \left(\dfrac{1}{2} \text{i}\right)^n (- 4 - 2\text{i}).\]
   Démontrons ce résultat par récurrence.
   Initialisation : Si $n=0$ alors $u_0=z_0-z_A=-4-2\text{i}$
   $\left(\dfrac{1}{2}\text{i}\right)^0(-4-2\text{i})=-4-2\text{i}$.
   La propriété est donc vraie au rang $0$.
   $\quad$
   Hérédité : Supposons la propriété vraie au rang $n$ : $u_n=\left(\dfrac{1}{2}\text{i}\right)^n(-4-2\text{i})$
   Alors :
   $\begin{align*} u_{n+1}&=\dfrac{1}{2}\text{i} \times u_n \\
   &=\dfrac{1}{2}\text{i} \times \left(\dfrac{1}{2}\text{i}\right)^n(-4-2\text{i}) \\
   &= \left(\dfrac{1}{2}\text{i}\right)^{n+1}(-4-2\text{i})
   \end{align*}$
   La propriété est donc vraie au rang $n+1$.
   $\quad$
   Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
   Par conséquent, pour tout entier naturel $n$ on a $u_n=\left(\dfrac{1}{2}\text{i}\right)^n(-4-2\text{i})$.
2. Démontrer que, pour tout entier naturel $n$, les points A, $M_n$ et $M_{n+4}$ sont alignés.
$\begin{align*} u_{n+4}&=\left(\dfrac{1}{2}\text{i}\right)^{n+4}(-4-2\text{i}) \\
&=\left(\dfrac{1}{2}\text{i}\right)^n \times \left(\dfrac{1}{2}\right)^4 \times (-4-2\text{i}) \\
&= u_n \times \dfrac{1}{2^4}
\end{align*}$
Or $u_n$ est l’affixe de $\vec{AM_n}$ et $u_{n+4}$ est l’affixe de $\vec{AM_{n+4}}$.
Ces deux vecteurs sont donc colinéaires et les points $A$, $M_n$ et $M_{n+4}$ sont alignés.