Baccalauréat S Métropole 22 juin 2015 - Correction Spécialité
Page 8 sur 10
Correction de l'exercice 4 5 points
- On considère l'équation (E) à résoudre dans \(\mathbb Z\) : \[7 x - 5 y = 1.\]
- Vérifier que le couple (3 ; 4) est solution de (E). $7 \times 3 – 5\times 4 = 21 – 20 = 1$
- Montrer que le couple d'entiers \((x ; y) \) est solution de (E) si et seulement si \(7(x - 3) = 5(y - 4)\). Soit $(x;y)$ un autre couple solution de $(E)$.
- Montrer que les solutions entières de l'équation CE) sont exactement les couples \((x~;~y)\) d'entiers relatifs tels que : \[\left\{\begin{array}{l c l} x &=&5k + 3\\ y &=&7k + 4 \end{array}\right.\:\text{ où } k \in \mathbb Z.\] $7$ et $5$ sont premiers entre eux.
Le couple $(3;4)$ est donc solution de $(E)$.
On a alors $7x – 5y = 1$ et $7 \times 3 – 5 \times 4 = 1$
Par différence on obtient :
$7(x-3) – 5(y – 4) = 0$
Donc $7(x-3) = 5(y-4)$
$\quad$
Réciproquement: soit $(x;y)$ un couple vérifiant $7(x-3) = 5(y-4)$
Alors $7x – 21 = 5y – 20$ donc $7x – 5y = 1$
$(x;y)$ est donc solution de $(E)$.
$\quad$
Le couple $(x;y)$ est solution de $(E)$ si, et seulement si, $7(x-3) = 5(y-4)$.
$\quad$
D’après le théorème de Gauss, il existe donc un entier relatif $k$ tel que :
$x-3 = 5k$ et $y-4 = 7k$ soit $x=3+5k$ et $y=4+7k$.
$\quad$
Réciproquement, soit $k$ un entier relatif
$7(5k+3) – 5(4+7k) = 35k + 21 – 20 – 35k = 1$
$\quad$
Les solutions de l’équation $(E)$ sont les couples $(x;y)$ d’entiers relatifs tels que $\begin{cases} x=5k+3 \\\\y=7k+4\end{cases} \qquad k\in \mathbb Z$. - Une boîte contient 25 jetons, des rouges, des verts et des blancs. Sur les 25 jetons il y a \(x\) jetons rouges et \(y\) jetons verts. Sachant que \(7x - 5 y = 1\), quels peuvent être les nombres de jetons rouges, verts et blancs ?
Dans la suite, on supposera qu'il y a 3 jetons rouges et 4 jetons verts. On cherche les valeurs de $k$ telles que $0 \le 5k + 3 \le 25$ et $0 \le 7k + 4 \le 25$ - On considère la marche aléatoire suivante d'un pion sur un triangle ABC. A chaque étape, on tire au hasard un des jetons parmi les 25, puis on le remet dans la boîte.
- Lorsqu'on est en A :
- Si le jeton tiré est rouge, le pion va en B. Si le jeton tiré est vert, le pion va en C. Si le jeton tiré est blanc, le pion reste en A.
- Si le jeton tiré est rouge, le pion va en A. Si le jeton tiré est vert, le pion va en C. Si le jeton tiré est blanc, le pion reste en B.
- Lorsqu'on est en C :
- Si le jeton tiré est rouge, le pion va en A. Si le jeton tiré est vert, le pion va en B. Si le jeton tiré est blanc, le pion reste en C.
- Au départ, le pion est sur le sommet A.
On note \(X_n\) la matrice ligne \(\begin{pmatrix}a_n& b_n& c_n\end{pmatrix}\) et \(T\) la matrice \(\begin{pmatrix}0,72 &0,12 &0,16\\ 0,12 &0,72 &0,16\\ 0,12& 0,16& 0,72\end{pmatrix}\).
Donner la matrice ligne \(X_0\) et montrer que, pour tout entier naturel \(n\), \(X_{n+1} = X_nT\). Comme au départ c'est-à-dire pour $n=0$, le pion est en A, on peut dire que $X_0 = \begin{pmatrix} 1&0&0 \end{pmatrix}$ - On admet que \(T = PDP^{-1}\) où \(P^{-1} = \begin{pmatrix}\frac{3}{10}&\frac{37}{110}&\frac{4}{11}\\ \frac{1}{10}&- \frac{1}{10}&0\\0&\frac{1}{11}&- \frac{1}{11}\end{pmatrix}\) et \(D = \begin{pmatrix}1&0&0&\\0&0,6&0\\0&0&0,56\end{pmatrix}\).
- À l'aide de la calculatrice, donner les coefficients de la matrice \(P\). On pourra remarquer qu'ils sont entiers. On a $P = \begin{pmatrix} 1&7&4 \\1&-3&4\\1&-3&-7\end{pmatrix}$
- Montrer que \(T^n = PD^nP^{-1}\). Raisonnons par récurrence :
- Donner sans justification les coefficients de la matrice \(D^n\). On note \(\alpha_n,\:\beta_n,\:\gamma_n\) les coefficients de la première ligne de la matrice \(T^n\) ainsi : \[T^n = \begin{pmatrix}\alpha_n&\beta_n&\gamma_n\\\ldots&\ldots&\ldots\\\ldots&\ldots&\ldots\end{pmatrix}.\]On admet que \(\alpha_n = \dfrac{3}{10} + \dfrac{7}{10} \times 0,6^n\) et \(\beta_n = \dfrac{37 - 77 \times 0,6^n + 40 \times 0,56^n}{110}\).
On ne cherchera pas à calculer les coefficients de la deuxième ligne ni ceux de la troisième ligne. $$D^n = \begin{pmatrix} 1&0&0 \\0&0,6^n&0\\0&0&0,56^n\end{pmatrix}$$
$\quad$
Initialisation : Si $n=0$ alors $PD^0P^{-1} = PP^{-1} = I_3 = D^0$
La propriété est vraie au rang $0$.
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $T^n=PD^nP^{-1}$
Alors $T^{n+1} = T^n T =$ $=PD^nP^{-1}PDP^{-1}$ $=PD^{n+1}P^{-1}$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ on a $T^n = PD^nP^{-1}$.
$\quad$
- On rappelle que, pour tout entier naturel \(n\), \(X_n = X_0T^n\).
- Déterminer les nombres \(a_n\), \(b_n\), à l'aide des coefficients \(\alpha_n\) et \(\beta_n\). En déduire \(c_n\). On a :
- Déterminer les limites des suites \(\left(a_n\right)\), \(\left(b_n\right)\) et \(\left(c_n\right)\). $0 < 0,6<1$ donc $\lim\limits_{n \to +\infty} 0,6^n = 0$ et $0 < 0,56 < 1$ donc $\lim\limits_{n \to +\infty} 0,56^n = 0$.
- Sur quel sommet a-t-on le plus de chance de se retrouver après un grand nombre d'itérations de cette marche aléatoire? On a $\dfrac{4}{11} > \dfrac{37}{110} > \dfrac{3}{10}$.
$a_n = 1 \times \alpha_n = \dfrac{3}{10} + \dfrac{7}{10} \times 0,6^n$
$\quad$
$b_n = 1 \times \beta_n = \dfrac{37 – 77 \times 0,6^n + 40 \times 0,56^n}{110}$
$\quad$
On sait que $a_n+b_n+c_n = 1$ donc
$$\begin{array}{rl} c_n &= 1 -a_n – b_n \\ &= \dfrac{7}{10} – \dfrac{7}{10}\times 0,6^n – \dfrac{37 – 77 \times 0,6^n + 40 \times 0,56^n}{110} \end{array}$$
Par conséquent $\lim\limits_{n \to +\infty} a_n = \dfrac{3}{10}$ et $\lim\limits_{n \to +\infty}b_n = \dfrac{37}{110}$
Ainsi $\lim\limits_{n \to +\infty} c_n = \dfrac{7}{10} – \dfrac{37}{110} = \dfrac{4}{11}$
Au bout d’un grand nombre d’itérations de cette marche aléatoire, on a plus de chance de se trouver sur le sommet $C$.
$0 \le 5k + 3 \le 25 \iff -3 \le 5k \le 22 \iff -\dfrac{3}{25} \le k \le \dfrac{22}{3}$ donc $k \in\lbrace0;1;2;3;4;5;6;7\rbrace$
$\quad$
$0 \le 7k + 4 \le 25 \iff -4 \le 7k \le 21 \iff -\dfrac{4}{7} \le k \le 3$ donc $k \in\lbrace 0;1;2;3 \rbrace$.
On veut de plus que $25 – (5k+3 + 7k + 4) \ge 0$ soit $18 – 12k \ge 0$ donc $k \in \lbrace 0;1 \rbrace$.
On peut donc avoir :
$3$ jetons rouges, $4$ jetons verts et $18$ jetons blancs $\quad$ ou $\quad$ $8$ jetons rouges, $11$ jetons verts et $6$ jetons blancs .
$\quad$
D'après le texte, on tire au hasard un pion dans la boîte, donc il y a équiprobabilité. Il y a 3 pions rouges sur 25 donc la probabilité de tirer un pion rouge est $\dfrac{3}{25}=0,12$.
On calcule de même la probabilité de tirer un pion vert: $\dfrac{4}{25}=0,16$ et la probabilité de tirer un pion blanc: $\dfrac{18}{25}=0,72$.
On cherche la probabilité $a_{n+1}$ qu'à l'étape $n+1$ le pion soit en A.
On peut représenter la situation à l'aide d'un arbre pondéré ;
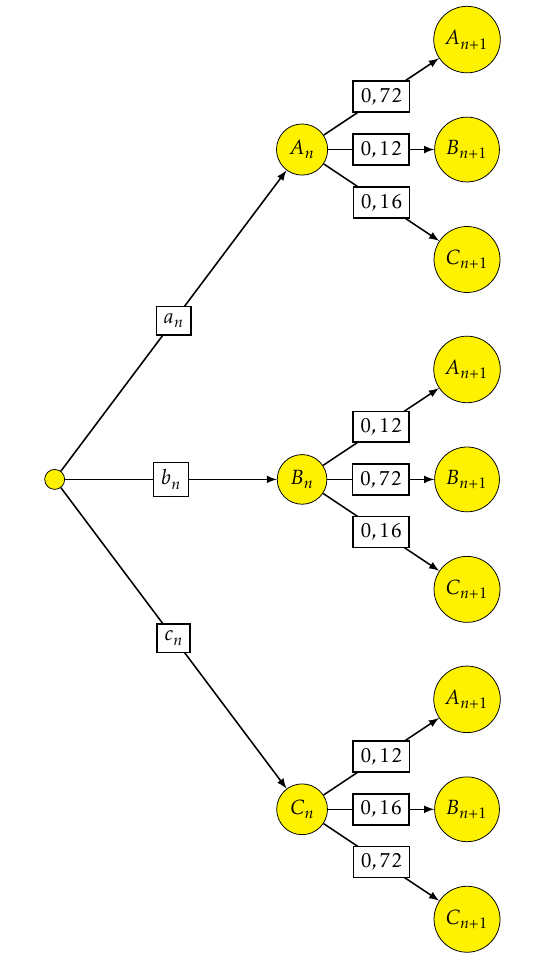
A chaque étape , en utilisant la formule des probabilités totales, on a :
$a_{n+1} = \dfrac{18}{25}a_n + \dfrac{3}{25} b_n + \dfrac{3}{25}c_n = 0,72a_n + 0,12b_n + 0,12c_n$
$\quad$
$b_{n+1} = \dfrac{3}{25}a_n + \dfrac{18}{25}b_n + \dfrac{4}{25}c_n = 0,12a_n+0,72b_n+0,16c_n$
$\quad$
$c_{n+1} = \dfrac{4}{25}a_n + \dfrac{4}{25}b_n + \dfrac{18}{25}c_n = 0,16a_n+0,16b_n+0,72c_n$
$\quad$
On a donc bien $X_{n+1} = X_nT$
- Vues: 27357
