Baccalauréat S Antilles Guyane 22 juin 2015 - Exercice 2

Page 3 sur 10: Exercice 2

Exercice 2 5 points

Commun à tous les candidats

La partie C peut être traitée indépendamment des parties A et B

Partie A

On considère une variable aléatoire $X$ qui suit la loi exponentielle de paramètre $\lambda$ avec $\lambda > 0$. On rappelle que, pour tout réel $a$ strictement positif, \[P(X \leqslant a) = \displaystyle\int_0^a \lambda\text{e}^{- \lambda t}\:\text{d}t.\] On se propose de calculer l'espérance mathématique de $X$, notée $E(X)$, et définie par \[E(X) = \displaystyle\lim_{x \to + \infty} \int_0^x \lambda t \text{e}^{- \lambda t}\:\text{d}t.\] On note $\mathbb R$ l'ensemble des nombres réels. On admet que la fonction $F$ définie sur $\mathbb R$ par $F(t) = - \left(t + \dfrac{1}{\lambda}\right)\text{e}^{- \lambda t}$ est une primitive sur $\mathbb R$ de la fonction $f$ définie sur $\mathbb R$ par $f(t) = \lambda t \text{e}^{- \lambda t}$.

1. Soit $x$ un nombre réel strictement positif. Vérifier que \[\displaystyle \int_0^x \lambda t \text{e}^{- \lambda t}\:\text{d}t = \dfrac{1}{\lambda}\left(- \lambda x \text{e}^{- \lambda x} - \text{e}^{- \lambda x} + 1\right).\]
2. En déduire que $E(X) = \dfrac{1}{\lambda}$.

 

Partie B

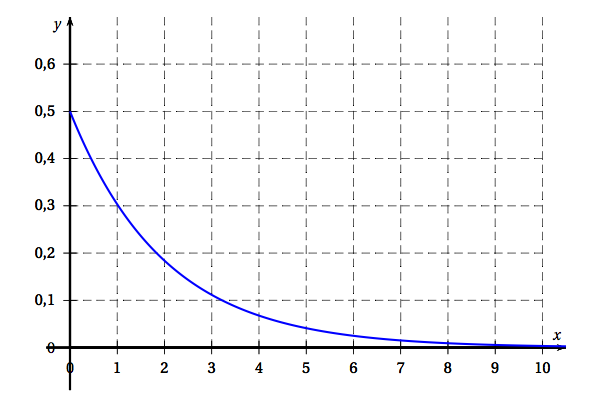
La durée de vie, exprimée en années, d'un composant électronique peut être modélisée par une variable aléatoire notée $X$ suivant la loi exponentielle de paramètre $\lambda$ avec $\lambda > 0$. La courbe de la fonction densité associée est représentée en \textbf{annexe 2}.

1. Sur le graphique de l'annexe 2 (à rendre avec la copie) :
   1. Représenter la probabilité $P(X \leqslant 1)$.
   2. Indiquer où se lit directement la valeur de $\lambda$.
2. On suppose que $E(X) = 2$.
   1. Que représente dans le cadre de l'exercice la valeur de l'espérance mathématique de la variable aléatoire $X$ ?
   2. Calculer la valeur de $\lambda$.
   3. Calculer $P(X \leqslant 2)$. On donnera la valeur exacte puis la valeur arrondie à $0,01$ près. Interpréter ce résultat.
   4. Sachant que le composant a déjà fonctionné une année, quelle est la probabilité que sa durée de vie totale soit d'au moins trois années ? On donnera la valeur exacte.

 

Partie C

Un circuit électronique est composé de deux composants identiques numérotés 1 et 2.
On note $D_1$ l'évènement « le composant 1 est défaillant avant un an »  et on note $D_2$ l'évènement « le composant 2 est défaillant avant un an ».
On suppose que les deux événements $D_1$ et $D_2$ sont indépendants et que $P\left(D_1\right) = P\left(D_2\right) = 0,39$.
Deux montages possibles sont envisagés, présentés ci-dessous :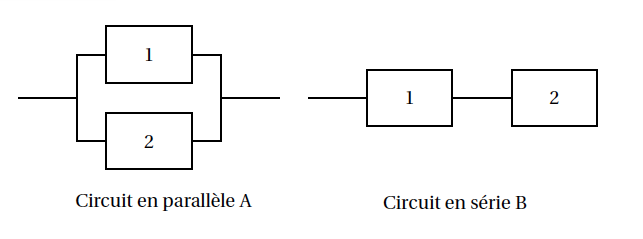

1. Lorsque les deux composants sont montés « en parallèle », le circuit A est défaillant uniquement si les deux composants sont défaillants en même temps. Calculer la probabilité que le circuit A soit défaillant avant un an.
2. Lorsque les deux composants sont montés « en série », le circuit B est défaillant dès que l'un au moins des deux composants est défaillant. Calculer la probabilité que le circuit B soit défaillant avant un an.

Annexe 2