Baccalauréat S Métropole- La Réunion 12 septembre 2016

 

Exercice 1 6 points

Commun à tous les candidats

Les trois parties sont indépendantes. Les résultats des probabilités seront arrondis à $10^{-3} $ près.

Partie 1

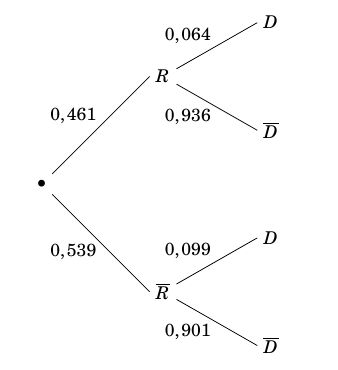
On estime qu'en 2013 la population mondiale est composée de 4,6 milliards de personnes âgées de 20 à 79 ans et que 46,1 % des personnes âgées de 20 à 79 ans vivent en zone rurale et 53,9 % en zone urbaine. En 2013, d'après la fédération internationale du diabète, 9,9 % de la population mondiale âgée de 20 à 79 ans vivant en zone urbaine est atteinte de diabète et 6,4 % de la population mondiale âgée de 20 à 79 ans vivant en zone rurale est atteinte de diabète. On interroge au hasard une personne âgée de 20 à 79 ans. On note :

• $R$ l'évènement : «la personne choisie habite en zone rurale » ,
• $D$ l'évènement: «la personne choisie est atteinte de diabète » .

 

1. Traduire cette situation à l'aide d'un arbre de probabilité.
2. 1. Calculer la probabilité que la personne interrogée soit diabétique.
   2. La personne choisie est diabétique. Quelle est la probabilité qu'elle habite en zone rurale ?

 

Partie 2

Une personne est dite en hypoglycémie si sa glycémie à jeun est inférieure à 60 mg.dL$^{-1}$ et elle est en hyperglycémie si sa glycémie à jeun est supérieure à 110 mg. dL$^{-1}$. La glycémie à jeun est considérée comme «normale »  si elle est comprise entre 70 mg.dL$^{-1}$ et 110 mg.dL$^{-1}$. Les personnes ayant un taux de glycémie compris entre 60 et 70 mg.dL$^{-1}$ ne font pas l'objet d'un suivi particulier. On choisit au hasard un adulte dans cette population. Une étude a permis d'établir que la probabilité qu'il soit en hyperglycémie est 0,052 à $10^{-3}$ près. Dans la suite on admettra que cette probabilité est égale à $0,052$. On modélise la glycémie à jeun, exprimée en mg.dL$^{-1}$, d'un adulte d'une population donnée, par une variable aléatoire $X$ qui suit une loi normale d'espérance $\mu$ et d'écart-type $\sigma$. On donne ci-dessous la représentation graphique de la densité de probabilité de la variable aléatoire $X$.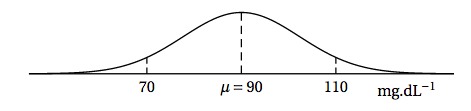

1. Quelle est la probabilité que la personne choisie ait une glycémie à jeun «normale»  ?
2. Déterminer la valeur de $\sigma$ arrondie au dixième.
3. Dans cette question, on prend $\sigma = 12$. Calculer la probabilité que la personne choisie soit en hypoglycémie.

 

Partie 3

Afin d'estimer la proportion, pour l'année 2013, de personnes diagnostiquées diabétiques dans la population française âgée de 20 à 79 ans, on interroge au hasard 10000 personnes. Dans l'échantillon étudié, 716 personnes ont été diagnostiquées diabétiques.

1. À l'aide d'un intervalle de confiance au niveau de confiance 95 % , estimer la proportion de personnes diagnostiquées diabétiques dans la population française âgée de 20 à 79 ans.
2. Quel doit être le nombre minimal de personnes à interroger si l'on veut obtenir un intervalle de confiance d'amplitude inférieure ou égale à 0,01 ?

 

 

 

Correction de l'exercice 1 (6 points)

Commun à tous les candidats

Les trois parties sont indépendantes. Les résultats des probabilités seront arrondis à $10^{-3} $ près.

Partie 1

On estime qu'en 2013 la population mondiale est composée de 4,6 milliards de personnes âgées de 20 à 79 ans et que 46,1 % des personnes âgées de 20 à 79 ans vivent en zone rurale et 53,9 % en zone urbaine. En 2013, d'après la fédération internationale du diabète, 9,9 % de la population mondiale âgée de 20 à 79 ans vivant en zone urbaine est atteinte de diabète et 6,4 % de la population mondiale âgée de 20 à 79 ans vivant en zone rurale est atteinte de diabète. On interroge au hasard une personne âgée de 20 à 79 ans. On note :

• $R$ l'évènement : «la personne choisie habite en zone rurale » ,
• $D$ l'évènement: «la personne choisie est atteinte de diabète » .

 

1. Traduire cette situation à l'aide d'un arbre de probabilité.

2. 1. Calculer la probabilité que la personne interrogée soit diabétique.
   D’après la formule des probabilités totales on a :
   $\begin{align*} p(D)&=p(D\cap R)+p\left(D\cap \overline{R}\right) \\ &=0,461\times 0,064+0,539\times 0,099
   &=0,082~865
   &\approx 0,083
   \end{align*}$
   $\quad$
   
   2. La personne choisie est diabétique. Quelle est la probabilité qu'elle habite en zone rurale ?
   On veut calculer :
   $\begin{align*} p_D(R)&=\dfrac{p(D \cap R)}{p(D)} \\ &\approx\dfrac{0,461 \times 0,064}{0,083} \\ &\approx 0,355
   \end{align*}$
   Remarque : On obtient environ $0,356$ quand on garde la valeur exacte trouvée à la question 2.a.
   

 

Partie 2

Une personne est dite en hypoglycémie si sa glycémie à jeun est inférieure à 60 mg.dL$^{-1}$ et elle est en hyperglycémie si sa glycémie à jeun est supérieure à 110 mg. dL$^{-1}$. La glycémie à jeun est considérée comme «normale »  si elle est comprise entre 70 mg.dL$^{-1}$ et 110 mg.dL$^{-1}$. Les personnes ayant un taux de glycémie compris entre 60 et 70 mg.dL$^{-1}$ ne font pas l'objet d'un suivi particulier. On choisit au hasard un adulte dans cette population. Une étude a permis d'établir que la probabilité qu'il soit en hyperglycémie est 0,052 à $10^{-3}$ près. Dans la suite on admettra que cette probabilité est égale à $0,052$. On modélise la glycémie à jeun, exprimée en mg.dL$^{-1}$, d'un adulte d'une population donnée, par une variable aléatoire $X$ qui suit une loi normale d'espérance $\mu$ et d'écart-type $\sigma$. On donne ci-dessous la représentation graphique de la densité de probabilité de la variable aléatoire $X$.

1. Quelle est la probabilité que la personne choisie ait une glycémie à jeun «normale»  ?
On veut calculer $P(70\leq X \leq 110)$.
On sait que $P(X > 110) = 0,052$.
Or $\mu=90$ donc $P(X<70)=P(X>110)$.
Ainsi
$\begin{align*} P(70\leq X \leq 110) &=1-P(X<70)-P(X>110) \\ &=1-0,052-0,052 \\ &=0,896
\end{align*}$

2. Déterminer la valeur de $\sigma$ arrondie au dixième.
On note $Z=\dfrac{X-90}{\sigma}$.
Cette variable aléatoire suit la loi normale centrée réduite.
$\begin{align*} P(70\leq X \leq 110) =0,896 &\iff P(-20 \leq X-90 \leq 20) = 0,896\\ &\iff P\left(-\dfrac{20}{\sigma} \leq \dfrac{X-90}{\sigma} \leq \dfrac{20}{\sigma}\right) = 0,896 \\ &\iff P\left(-\dfrac{20}{\sigma} \leq Z \leq \dfrac{20}{\sigma}\right) = 0,896 \\ &\iff 2P\left(Z \leq \dfrac{20}{\sigma}\right)-1= 0,896 \\ &\iff 2P\left(Z \leq \dfrac{20}{\sigma}\right)= 1,896 \\ &\iff P\left(Z \leq \dfrac{20}{\sigma}\right)= 0,948
\end{align*}$
Par conséquent, en utilisant la fonction inverse loi normale de la calculatrice, on trouve $\dfrac{20}{\sigma} \approx 1,626$.
Donc $\sigma \approx \dfrac{20}{1,626}$ soit $\sigma \approx 12,3$

3. Dans cette question, on prend $\sigma = 12$. Calculer la probabilité que la personne choisie soit en hypoglycémie.
La probabilité que la personne choisie soit en hypoglycémie est $P(X<60)$. À la calculatrice, pour la variable aléatoire $X$ qui suit la loi normale de paramètres $\mu=90$ et $\sigma=12$, on trouve $P(X < 60)\approx 0,006$. La probabilité, arrondie au millième, que la personne choisie soit en hypoglycémie est 0,006.

 

Partie 3

Afin d'estimer la proportion, pour l'année 2013, de personnes diagnostiquées diabétiques dans la population française âgée de 20 à 79 ans, on interroge au hasard 10000 personnes. Dans l'échantillon étudié, 716 personnes ont été diagnostiquées diabétiques.

1. À l'aide d'un intervalle de confiance au niveau de confiance 95 % , estimer la proportion de personnes diagnostiquées diabétiques dans la population française âgée de 20 à 79 ans.
La fréquence observée est $f=\dfrac{716}{10~000}=0,071~6$
Un intervalle de confiance au niveau de confiance $95\%$ est :
$\begin{align*} I_{10~000}&=\left[0,071~6-\dfrac{1}{\sqrt{10~000}};0,071~6+\dfrac{1}{\sqrt{10~000}} \right] \\ &=[0,061~6;0,0816]
\end{align*}$

2. Quel doit être le nombre minimal de personnes à interroger si l'on veut obtenir un intervalle de confiance d'amplitude inférieure ou égale à 0,01 ?
On appelle $n$ la taille de l’échantillon étudié pour un caractère dont la fréquence d’apparition est $f$.
L’amplitude de l’intervalle de confiance est alors :
$\begin{align*} A&=f+\dfrac{1}{\sqrt{n}}-\left(f-\dfrac{1}{\sqrt{n}}\right) \\ &=\dfrac{2}{\sqrt{n}}
\end{align*}$
On veut donc que :
$\begin{align*} \dfrac{2}{\sqrt{n}} \leq 0,01 &\iff \sqrt{n}\geq \dfrac{2}{0,01} \\ &\iff \sqrt{n} \geq 200 \\ &\iff n\geq 40~000
\end{align*}$
Il faut donc interroger au moins $40~000$ personnes.

Exercice 2 3 points

Commun à tous les candidats

On considère les nombres complexes $z_n$ définis pour tout entier $n \geqslant 0$ par la donnée de $z_0$, où $z_0$ est différent de 0 et de 1, et la relation de récurrence: \[z_{n+1} = 1- \dfrac{1}{z_n}.\]

1. 1. Dans cette question, on suppose que $z_0 = 2$. Déterminer les nombres $z_1$, $z_2$, $z_3$, $z_4$, $z_5$ et $z_6$
   2. Dans cette question, on suppose que $z_0 = \text{i}$. Déterminer la forme algébrique des nombres complexes $z_1$, $z_2$, $z_3$, $z_4$, $z_5$ et $z_6$.
   3. Dans cette question on revient au cas général où $z_0$ est un complexe donné. Que peut-on conjecturer pour les valeurs prises par $z_{3n}$ selon les valeurs de l'entier naturel $n$ ? Prouver cette conjecture.
2. Déterminer $z_{ 2016 }$ dans le cas où $z_0 = 1 + \text{i}$.
3. Existe-t-il des valeurs de $z_0$ tel que $z_0 = z_1$ ? Que peut-on dire de la suite $\left(z_n\right)$ dans ce cas ?

Correction de l'exercice 2 (3 points)

Commun à tous les candidats

On considère les nombres complexes $z_n$ définis pour tout entier $n \geqslant 0$ par la donnée de $z_0$, où $z_0$ est différent de 0 et de 1, et la relation de récurrence: \[z_{n+1} = 1- \dfrac{1}{z_n}.\]

1. 1. Dans cette question, on suppose que $z_0 = 2$. Déterminer les nombres $z_1$, $z_2$, $z_3$, $z_4$, $z_5$ et $z_6$
   Si $z_0=2$ alors $z_1 = 1-\dfrac{1}{2} = \dfrac{1}{2}$
   $z_2=1-\dfrac{1}{\dfrac{1}{2}}=-1$
   $z_3=1-\dfrac{1}{-1}=2$
   $z_4=\dfrac{1}{2}$
   $z_5=-1$
   $z_6=2$
   $\quad$
   
   2. Dans cette question, on suppose que $z_0 = \text{i}$. Déterminer la forme algébrique des nombres complexes $z_1$, $z_2$, $z_3$, $z_4$, $z_5$ et $z_6$.
   Si $z_0=\text{i}$ alors $z_1=1-\dfrac{1}{\text{i}}=1+\text{i}$
   $z_2=1-\dfrac{1}{1+\text{i}} = \dfrac{1}{2}+\dfrac{\text{i}}{2}$
   $z_3=1-\dfrac{1}{\dfrac{1}{2}+\dfrac{\text{i}}{2}}=\text{i}$
   $z_4=1+\text{i}$
   $z_5=\dfrac{1}{2}+\dfrac{\text{i}}{2}$
   $z_6=\text{i}$
   $\quad$
   
   3. Dans cette question on revient au cas général où $z_0$ est un complexe donné. Que peut-on conjecturer pour les valeurs prises par $z_{3n}$ selon les valeurs de l'entier naturel $n$ ? Prouver cette conjecture.
   On peut conjecturer que, pour tout entier naturel $n$, on a $z_{3n}=z_0$
   Initialisation : Si $n=0$ alors $z_{3n}=z_{3\times 0}=z_0$.
   La propriété est vraie au rang $n$.
   $\quad$
   Hérédité : Supposons la propriété vraie au rang $n$ : $z_{3n}=z_0$.
   $z_{3n+1}=1-\dfrac{1}{z_0}=\dfrac{z_0-1}{z_0}$
   $z_{3n+2}=1-\dfrac{1}{\dfrac{z_0-1}{z_0}} = 1-\dfrac{z_0}{z_0-1}=\dfrac{-1}{z_0-1}$
   $z_{3n+3}=1-\dfrac{1}{\dfrac{-1}{z_0-1}} = 1+z_0-1=z_0$
   Par conséquent $z_{3(n+1)}=z_0$.
   La propriété est vraie au rang $n+1$
   $\quad$
   Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
   Par conséquent, pour tout entier naturel $n$, on a $z_{3n}=z_0$.
   $\quad$
2. Déterminer $z_{ 2016 }$ dans le cas où $z_0 = 1 + \text{i}$.
$2016=3\times 672$ donc $z_{2016}=z_0=1+\text{i}$.
$\quad$
3. Existe-t-il des valeurs de $z_0$ tel que $z_0 = z_1$ ? Que peut-on dire de la suite $\left(z_n\right)$ dans ce cas ?
On cherche la valeur de $z_0$ telle que :
$\begin{align*} z_0=1-\dfrac{1}{z_0} &\iff \dfrac{z_0^2-z_0+1}{z_0} = 0\\ &\iff z_0^2-z_0+1=0 \text{ et } z_0\neq  0
\end{align*}$
$\Delta = -3 <0$
Il y a donc deux solutions complexes : $\dfrac{1-\text{i}\sqrt{3}}{2}$ et $\dfrac{1+\text{i}\sqrt{3}}{2}$.
Par conséquent si $z_0 \in \left\{\dfrac{1-\text{i}\sqrt{3}}{2};\dfrac{1+\text{i}\sqrt{3}}{2}\right\}$ alors $z_0=z_1$.
La suite $\left(z_n\right)$ est alors stationnaire.

Exercice 3 5 points

Probabilités et suites

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

On dispose d'un dé équilibré à 6 faces numérotées de 1 à 6 et de 2 pièces A et B ayant chacune un côté pile et un côté face. Un jeu consiste à lancer une ou plusieurs fois le dé. Après chaque lancer de dé, si l'on obtient 1 ou 2, alors on retourne la pièce A, si l'on obtient 3 ou 4, alors on retourne la pièce B et si l'on obtient 5 ou 6, alors on ne retourne aucune des deux pièces. Au début du jeu, les 2 pièces sont du côté face.

1. Dans l'algorithme ci-dessous, 0 code le côté face d'une pièce et 1 code le côté pile. Si $a$ code le côté de la pièce A à un instant donné, alors $1 - a$ code le côté de la pièce A après l'avoir retournée. $$\begin{array}{|ll|}\hline \text{Variables :} & a, b, d, s \text{sont des entiers}\\ & i, n \text{sont des entiers supérieurs ou égaux à } 1\\ \text{Initialisation :}& a \text{ prend la valeur } 0\\ & b \text{ prend la valeur } 0\\ &\text{Saisir } n\\ \text{Traitement :} & \text{Pour } i \text{ allant de 1 à } n \text{ faire }\\ &\begin{array}{|l} d \text{ prend la valeur d'un entier aléatoire compris } \\ \text{entre 1 et 6 }\\ \text{Si } d \leqslant 2\\ \hspace{0.5cm} \begin{array}{|l} \text{alors } a \text{ prend la valeur } 1 - a\\ \text{sinon Si } d \leqslant 4\\ \hspace{1.5cm}| \text{alors } b \text{ prend la valeur } 1 - b\\ \hspace{1cm}\text{FinSi }\\ \end{array}\\ \text{FinSi}\\ s \text{ prend la valeur } a + b\\ \end{array}\\ &\text{ FinPour }\\ \text{Sortie :}&\text{ Afficher } s\\ \hline \end{array}$$
   1. On exécute cet algorithme en saisissant $n = 3$ et en supposant que les valeurs aléatoires générées successivement pour $d$ sont 1 ; 6 et 4. Recopier et compléter le tableau donné ci-dessous contenant l'état des variables au cours de l'exécution de l'algorithme :
        $$\begin{array}{|l|c|c|c|c|c|} \hline \text{variables}&i&d&a&b&s\\ \hline \text{initialisation}&\text{X}&\text{X}& & &\text{X}\\ \hline 1^{ er}\text{ passage boucle Pour}&& & & & \\ \hline 2^{ e}\text{ passage boucle Pour}& & & & & \\ \hline 3^{ e}\text{ passage boucle Pour}& && & & \\ \hline \end{array}$$
   2. Cet algorithme permet-il de décider si à la fin les deux pièces sont du côté pile ?
2. Pour tout entier naturel $n$, on note :
   $\bullet~~$ $X_n$ l'évènement : « À l'issue de $n$ lancers de dés, les deux pièces sont du côté face»
   $\bullet~~$ $Y_n$ l'évènement : « À l'issue de $n$ lancers de dés, une pièce est du côté pile et l'autre est du côté face»
   $\bullet~~$ $Z_n$ l'évènement : « À l'issue de $n$ lancers de dés, les deux pièces sont du côté pile».
   De plus on note, $x_n = P\left(X_n\right)$ ; $y_n = P\left(Y_n\right)$ et $z_n = P\left(Z_n\right)$ les probabilités respectives des évènements $X_n$, $Y_n$ et $Z_n$.
   1. Donner les probabilités $x_0$ , $y_0$ et $z_0$ respectives qu'au début du jeu il y ait 0, 1 ou 2 pièces du côté pile.
   2. Justifier que $P_{X_n}\left(X_{n+1}\right) = \dfrac{1}{3}$.
   3. Recopier l'arbre ci-dessous et compléter les probabilités sur ses branches, certaines pouvant être nulles :
      
   4. Pour tout entier naturel $n$, exprimer $z_n$ en fonction de $x_n$ et $y_n$.
   5. En déduire que, pour tout entier naturel $n$, $y_{n+1} = - \dfrac{1}{3}y_n + \dfrac{2}{3}$.
   6. On pose, pour tout entier naturel $n$, $b_n = y_n - \dfrac{1}{2}$. Montrer que la suite $\left(b_n\right)$ est géométrique. En déduire que, pour tout entier naturel $n$, $y_n = \dfrac{1}{2} - \dfrac{1}{2}\times \left(- \dfrac{1}{3}\right)^n$.
   7. Calculer $\displaystyle\lim_{n \to + \infty} y_n$. Interpréter le résultat.

 

Correction de l'exercice 3 (5 points)

Probabilités et suites

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

On dispose d'un dé équilibré à 6 faces numérotées de 1 à 6 et de 2 pièces A et B ayant chacune un côté pile et un côté face. Un jeu consiste à lancer une ou plusieurs fois le dé. Après chaque lancer de dé, si l'on obtient 1 ou 2, alors on retourne la pièce A, si l'on obtient 3 ou 4, alors on retourne la pièce B et si l'on obtient 5 ou 6, alors on ne retourne aucune des deux pièces. Au début du jeu, les 2 pièces sont du côté face.

1. Dans l'algorithme ci-dessous, 0 code le côté face d'une pièce et 1 code le côté pile. Si $a$ code le côté de la pièce A à un instant donné, alors $1 - a$ code le côté de la pièce A après l'avoir retournée. $$\begin{array}{|ll|}\hline \text{Variables :} & a, b, d, s \text{sont des entiers}\\ & i, n \text{sont des entiers supérieurs ou égaux à } 1\\ \text{Initialisation :}& a \text{ prend la valeur } 0\\ & b \text{ prend la valeur } 0\\ &\text{Saisir } n\\ \text{Traitement :} & \text{Pour } i \text{ allant de 1 à } n \text{ faire }\\ &\begin{array}{|l} d \text{ prend la valeur d'un entier aléatoire compris } \\ \text{entre 1 et 6 }\\ \text{Si } d \leqslant 2\\ \hspace{0.5cm} \begin{array}{|l} \text{alors } a \text{ prend la valeur } 1 - a\\ \text{sinon Si } d \leqslant 4\\ \hspace{1.5cm}| \text{alors } b \text{ prend la valeur } 1 - b\\ \hspace{1cm}\text{FinSi }\\ \end{array}\\ \text{FinSi}\\ s \text{ prend la valeur } a + b\\ \end{array}\\ &\text{ FinPour }\\ \text{Sortie :}&\text{ Afficher } s\\ \hline \end{array}$$
   1. On exécute cet algorithme en saisissant $n = 3$ et en supposant que les valeurs aléatoires générées successivement pour $d$ sont 1 ; 6 et 4. Recopier et compléter le tableau donné ci-dessous contenant l'état des variables au cours de l'exécution de l'algorithme : $$\begin{array}{|l|c|c|c|c|c|} \hline \text{variables}&i&d&a&b&s\\ \hline \text{initialisation}&\text{X}&\text{X}& & &\text{X}\\ \hline 1^{ er}\text{ passage boucle Pour}&& & & & \\ \hline 2^{ e}\text{ passage boucle Pour}& & & & & \\ \hline 3^{ e}\text{ passage boucle Pour}& && & & \\ \hline \end{array}$$
   $$\begin{array}{|l|c|c|c|c|c|} \hline \text{variables}&i&d&a&b&s\\ \hline \text{initialisation}&\text{X}&\text{X}&0&0&\text{X}\\ \hline 1^{ er}\text{ passage boucle Pour}&1&1&1&0&1\\ \hline 2^{ e}\text{ passage boucle Pour}&2&6&1&1&2\\ \hline 3^{ e}\text{ passage boucle Pour}&3&4&1&0&1\\ \hline \end{array}$$
   2. Cet algorithme permet-il de décider si à la fin les deux pièces sont du côté pile ?
   A chaque étape la variable $s$ détermine le nombre de pièces se trouvant du côté pile.
   Cet algorithme permet donc bien de décider si à la fin les deux pièces sont du côté pile.
2. Pour tout entier naturel $n$, on note :
   $\bullet~~$ $X_n$ l'évènement : « À l'issue de $n$ lancers de dés, les deux pièces sont du côté face»
   $\bullet~~$ $Y_n$ l'évènement : « À l'issue de $n$ lancers de dés, une pièce est du côté pile et l'autre est du côté face»
   $\bullet~~$ $Z_n$ l'évènement : « À l'issue de $n$ lancers de dés, les deux pièces sont du côté pile».
   De plus on note, $x_n = P\left(X_n\right)$ ; $y_n = P\left(Y_n\right)$ et $z_n = P\left(Z_n\right)$ les probabilités respectives des évènements $X_n$, $Y_n$ et $Z_n$.
   1. Donner les probabilités $x_0$ , $y_0$ et $z_0$ respectives qu'au début du jeu il y ait 0, 1 ou 2 pièces du côté pile.
   $P\left(X_0\right)=1$, $P\left(Y_0\right)=0$ et $P\left(Z_0\right)=0$
   $\quad$
   
   2. Justifier que $P_{X_n}\left(X_{n+1}\right) = \dfrac{1}{3}$.
   On appelle $D$ la variable indiquant la face du dé obtenue.
   $P_{X_n}\left(X_{n+1}\right)=P\left(D\in\left\{5;6\right\}\right) = \dfrac{2}{6}=\dfrac{1}{3}$.
   
   3. Recopier l'arbre ci-dessous et compléter les probabilités sur ses branches, certaines pouvant être nulles :
      
   Si les pièces sont du côté face alors au bout de $n$ lancers alors, au lancer $n+1$, soit les pièces sont du côté face, soit une est du côté pile et l’autre du côté face.
   Par conséquent $P\left(X_n\cap Y_{n+1}\right)=1-\dfrac{1}{3} = \dfrac{2}{3}$.
   $\quad$
   Si, au lancer $n$, une pièce est du côté pile et l’autre est du côté face, alors la seule possibilité de conserver un tel état, au lancer $n+1$, est d’obtenir $5$ ou $6$ avec le dé.
   Donc $P\left(Y_n\cap Y_{n+1}\right)=\dfrac{1}{3}$.
   De même $P\left(Y_n\cap X_{n+1}\right) =\dfrac{1}{3}$ et $P\left(Y_n\cap Z_{n+1}\right)=\dfrac{1}{3}$
   $\quad$
   Si, au lancer $n$, les deux pièces sont du côté pile alors, au lancer $n+1$, on ne peut avoir que deux possibilités : les deux pièces sont toujours du côté pile ou alors l’une est du côté pile et l’autre du côté face.
   Pour garder les pièces du côté pile il faut obtenir $5$ ou $6$ avec le dé.
   Donc $P\left(Z_n\cap Z_{n+1}\right)=\dfrac{1}{3}$ et $P\left(Z_n\cap Y_{n+1}\right)=\dfrac{2}{3}$
   $\quad$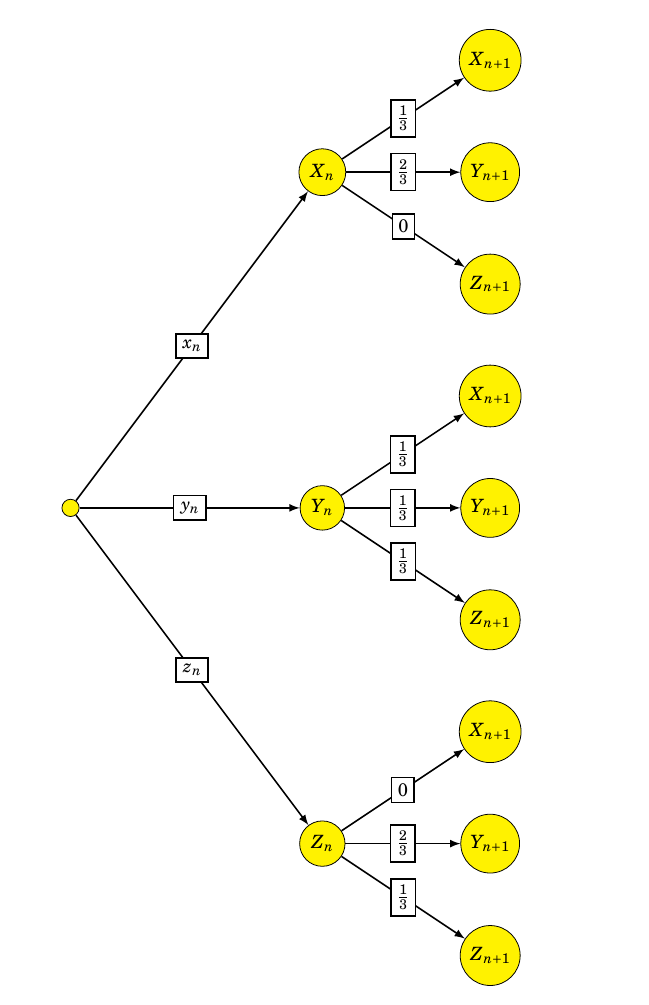
   
   4. Pour tout entier naturel $n$, exprimer $z_n$ en fonction de $x_n$ et $y_n$.
   Pour tout entier naturel $n$, on a $x_n+y_n+z_n=1$ donc $z_n=1-x_n-y_n$.
   $\quad$
   
   5. En déduire que, pour tout entier naturel $n$, $y_{n+1} = - \dfrac{1}{3}y_n + \dfrac{2}{3}$.
   D’après la formule des probabilité totale on a :
   $\begin{align*} y_{n+1}&=P\left(Y_{n+1}\right) \\ &=P\left(X_n\cap Y_{n+1}\right)+P\left(Y_n\cap Y_{n+1}\right)+P\left(Z_n\cap Y_{n+1}\right) \\ &=\dfrac{2}{3}x_n+\dfrac{1}{3}y_n+\dfrac{2}{3}z_n \\ &=\dfrac{2}{3}x_n+\dfrac{1}{3}y_n+\dfrac{2}{3}\left(1-x_n-y_n\right) \\ &=-\dfrac{1}{3}y_n+\dfrac{2}{3}
   \end{align*}$
   6. On pose, pour tout entier naturel $n$, $b_n = y_n - \dfrac{1}{2}$. Montrer que la suite $\left(b_n\right)$ est géométrique. En déduire que, pour tout entier naturel $n$, $y_n = \dfrac{1}{2} - \dfrac{1}{2}\times \left(- \dfrac{1}{3}\right)^n$.
   Pour tout entier naturel $n$ on a :
   $\begin{align*} b_{n+1}&=y_{n+1}-\dfrac{1}{2} \\ &=-\dfrac{1}{3}y_n+\dfrac{2}{3}-\dfrac{1}{2} \\ &=-\dfrac{1}{3}y_n+\dfrac{1}{6} \\ &=-\dfrac{1}{3}\left(y_n-\dfrac{1}{2}\right)
   \end{align*}$
   La suite $\left(b_n\right)$ est donc géométrique de raison $-\dfrac{1}{3}$ et de premier terme $b_0=0-\dfrac{1}{2}=-\dfrac{1}{2}$
   Par conséquent $b_n=-\dfrac{1}{2}\times \left(-\dfrac{1}{3}\right)^n$
   Et $y_n=b_n+\dfrac{1}{2}=\dfrac{1}{2}-\dfrac{1}{2}\times \left(-\dfrac{1}{3}\right)^n$
   $\quad$
   
   7. Calculer $\displaystyle\lim_{n \to + \infty} y_n$. Interpréter le résultat.
   $-1<-\dfrac{1}{3}<1$ donc $\lim\limits_{n \to +\infty} \left(-\dfrac{1}{3}\right)^n=0$
   Ainsi $\lim\limits_{n \to +\infty} y_n=\dfrac{1}{2}$.
   $\quad$
   Cela signifie donc, qu’au bout d’un grand nombre de lancers, la probabilité d’obtenir une pièce du côté pile et une du côté face est de $50\%$.
   $\quad$

 

Exercice 4 5 points

Commun à tous les candidats

Un hélicoptère est en vol stationnaire au-dessus d'une plaine. Un passager lâche verticalement un colis muni d'un parachute.

Partie 1

Soit $v_1$ la fonction définie sur $[0~;~+\infty[$ par : \[v_1(t) = 5 \times \dfrac{\text{e}^{0,3t} - 1}{\text{e}^{0,3t} + 1}.\]

1. Déterminer le sens de variation de la fonction $v_1$.
2. On suppose, dans cette question, que le parachute fonctionne correctement. On admet que $t$ secondes après qu'il a été lâché, la vitesse du colis (exprimée en m.s$^{-1}$) est égale, avant d'atteindre le sol, à $v_1(t)$. On considère que le colis arrive en bon état sur le sol si sa vitesse à l'arrivée n'excède pas 6 m.s$^{-1}$. Le colis risque-t-il d'être endommagé lorsque le parachute s'ouvre correctement ? Justifier.

Partie 2

On suppose, dans cette partie, que le parachute ne s'ouvre pas. On admet que, dans ce cas, avant que le colis atteigne le sol, sa vitesse (exprimée en m.s$^{-1}$), $t$ secondes après avoir été lâché par le passager, est donnée par : \[v_2(t) = 32,7 \left(1 - \text{e}^{- 0,3t}\right).\]

1. Quelle est la vitesse, exprimée en m.s$^{-1}$, atteinte par le colis au bout de 10 secondes ? Arrondir à 0,1 m.s$^{-1}$.
2. Résoudre l'équation $v_2(t) = 30$ m.s$^{-1}$. Donner une interprétation concrète de la solution de cette équation dans le cadre de cet exercice.
3. On sait que la chute du colis dure 20 secondes. On admet que la distance, en mètres, qui sépare l'hélicoptère du colis, $T$ secondes après avoir été lâché par le passager, est donnée par: \[d(T) = \displaystyle\int_0^T v_2(t)\:\text{d}t.\]
   1. Montrer que, pour tout réel $T$ de l'intervalle [0 ; 20], $d(T) = 109\left(\text{e}^{- 0,3 T} + 0,3 T - 1\right)$.
   2. Déterminer une valeur approchée à 1 m près de la distance parcourue par le colis lorsqu'il atteint le sol.
4. Déterminer un encadrement d'amplitude $0,1$~s du temps mis par le colis pour atteindre le sol si on l'avait lâché d'une hauteur de $700$ mètres.

 

Correction de l'exercice 4 5 points

Commun à tous les candidats

Un hélicoptère est en vol stationnaire au-dessus d'une plaine. Un passager lâche verticalement un colis muni d'un parachute.

Partie 1

Soit $v_1$ la fonction définie sur $[0~;~+\infty[$ par : \[v_1(t) = 5 \times \dfrac{\text{e}^{0,3t} - 1}{\text{e}^{0,3t} + 1}.\]

1. Déterminer le sens de variation de la fonction $v_1$.
La fonction $v_1$ est dérivable sur $[0;+\infty[$ en tant que quotient de fonctions dérivables sur cet intervalle dont le dénominateur ne s’annule pas.
$\begin{align*} v_1′(t)&=5\times \dfrac{0,3\text{e}^{0,3t}\left(e^{0,3t}+1\right)-0,3\text{e}^{0,3t}\left(\text{e}^{0,3t}-1\right)}{\left(\text{e}^{0,3t}+1\right)^2} \\ &=5\times 0,3 \times \dfrac{\text{e}^{0,6t}+\text{e}^{0,3t}-\text{e}^{0,6t}+\text{e}^{0,3t}}{\left(\text{e}^{0,3t}+1\right)^2}\\ &=1,5 \times \dfrac{2\times \text{e}^{0,3t}}{\left(\text{e}^{0,3t}+1\right)^2} \\ &=3\times \dfrac{\text{e}^{0,3t}}{\left(\text{e}^{0,3t}+1\right)^2} \\ &>0
\end{align*}$
La fonction exponentielle étant effectivement strictement positive sur $\mathbb R$ et donc sur $[0;+\infty[$.
$\quad$
Par conséquent la fonction $v_1$ est strictement croissante sur $[0;+\infty[$.
$\quad$
2. On suppose, dans cette question, que le parachute fonctionne correctement. On admet que $t$ secondes après qu'il a été lâché, la vitesse du colis (exprimée en m.s$^{-1}$) est égale, avant d'atteindre le sol, à $v_1(t)$. On considère que le colis arrive en bon état sur le sol si sa vitesse à l'arrivée n'excède pas 6 m.s$^{-1}$. Le colis risque-t-il d'être endommagé lorsque le parachute s'ouvre correctement ? Justifier.
On va donc déterminer $\lim\limits_{t \to +\infty} 5 \times \dfrac{\text{e}^{0,3t}-1}{\text{e}^{0,3t}+1}$.
$\dfrac{\text{e}^{0,3t}-1}{\text{e}^{0,3t}+1} = \dfrac{\text{e}^{0,3t}\left(1-\text{e}^{-0,3t}\right)}{\text{e}^{0,3t}\left(1+\text{e}^{-0,3t}\right)}=\dfrac{1-\text{e}^{-0,3t}}{1+\text{e}^{-0,3t}}$
Or $\lim\limits_{t \to +\infty} \text{e}^{-0,3t}=0$
Donc $\lim\limits_{t \to +\infty} \dfrac{\text{e}^{0,3t}-1}{\text{e}^{0,3t}+1} = 5$ et $\lim\limits_{t \to +\infty} v_1(t)=5$.
La fonction $v_1$ est strictement croissante et sa limite en $+\infty$ est $5$.
Par conséquent, pour tout $t \geq 0$, on a $v_1(t)\leq 5$.
Le colis ne sera donc pas endommagé lorsque le colis s’ouvre correctement.
$\quad$

Partie 2

On suppose, dans cette partie, que le parachute ne s'ouvre pas. On admet que, dans ce cas, avant que le colis atteigne le sol, sa vitesse (exprimée en m.s$^{-1}$), $t$ secondes après avoir été lâché par le passager, est donnée par : \[v_2(t) = 32,7 \left(1 - \text{e}^{- 0,3t}\right).\]

1. Quelle est la vitesse, exprimée en m.s$^{-1}$, atteinte par le colis au bout de 10 secondes ? Arrondir à 0,1 m.s$^{-1}$.
$v_2(10)=32,7\left(1-\text{e}^{-3}\right) \approx 31,1$ m.s$^{-1}$.
$\quad$
2. Résoudre l'équation $v_2(t) = 30$ m.s$^{-1}$. Donner une interprétation concrète de la solution de cette équation dans le cadre de cet exercice.
$\quad$
$\begin{align*} v_2(t)=30 &\iff 32,7\left(1-\text{e}^{-0,3t}\right) = 30 \\ &\iff 1-\text{e}^{-0,3t}=\dfrac{30}{32,7} \\ &\iff -\text{e}^{-0,3t}=\dfrac{30}{32,7}-1\\ &\iff \text{e}^{-0,3t}=\dfrac{2,7}{32,7}\\ &\iff -0,3t=\ln \dfrac{2,7}{32,7}\\ &\iff t=\dfrac{\ln \dfrac{2,7}{32,7}}{-0,3}
\end{align*}$
Par conséquent $t\approx 8,3$ s.
Cela signifie qu’au bout de $8,3$ secondes environ le colis a atteint la vitesse de $30$ m.s$^{-1}$.
$\quad$
3. On sait que la chute du colis dure 20 secondes. On admet que la distance, en mètres, qui sépare l'hélicoptère du colis, $T$ secondes après avoir été lâché par le passager, est donnée par: \[d(T) = \displaystyle\int_0^T v_2(t)\:\text{d}t.\]
   1. Montrer que, pour tout réel $T$ de l'intervalle [0 ; 20], $d(T) = 109\left(\text{e}^{- 0,3 T} + 0,3 T - 1\right)$.
   
   $\begin{align*} d(T)&=\int_0^T v_2(t)\text{d}t \\ &=\int_0^T \left(32,7-32,7\text{e}^{-0,3t}\right)\text{d}t \\ &=\left[32,7t-\dfrac{32,7}{-0,3}\text{e}^{-0,3t}\right]_0^T \\ &=32,7T+109\text{e}^{-0,3T}-109 \\ &=109\left(\text{e}^{-0,3T}+0,3T-1\right)
   \end{align*}$
   $\quad$
   
   2. Déterminer une valeur approchée à 1 m près de la distance parcourue par le colis lorsqu'il atteint le sol.
   On veut calculer $d(20) = 109\left(\text{e}^{-6}+6-1\right) = 109\left(\text{e}^{-6}+5\right)\approx 545$ m.
   Le colis a donc parcouru environ $545$ mètres avant d’atteindre le sol.
   $\quad$
4. Déterminer un encadrement d'amplitude $0,1$~s du temps mis par le colis pour atteindre le sol si on l'avait lâché d'une hauteur de $700$ mètres.
On veut résoudre l’équation $d(T)=700$
Soit $109\left(\text{e}^{-0,3T}+0,3T-1\right)=700$
A l’aide de la fonction table de la calculatrice on trouve $\approx 24,7 < T <24,8$.
$\quad$

 

Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

On dispose d'un dé équilibré à 6 faces numérotées de 1 à 6 et de 3 pièces A, B et C ayant chacune un côté pile et un côté face. Un jeu consiste à lancer une ou plusieurs fois le dé. Après chaque lancer de dé, si l'on obtient 1 ou 2, alors on retourne la pièce A, si l'on obtient 3 ou 4, alors on retourne la pièce B et si l'on obtient 5 ou 6, alors on retourne la pièce C. Au début du jeu, les 3 pièces sont toutes du côté face.

1. Dans l'algorithme ci-dessous, 0 code le côté face et 1 code le côté pile. Si $a$ code un côté de la pièce A, alors $1 - a$ code l'autre côté de la pièce A. $$\begin{array}{|ll|}\hline \text{Variables :} &a, b, c, d, s\text{ sont des entiers naturels}\\ &i, n \text{ sont des entiers supérieurs ou égaux à } 1\\ \text{Initialisation :}&a \text{ prend la valeur }0\\ &b\text{ prend la valeur }0\\ &c \text{ prend la valeur }0\\ &\text{Saisir }n\\ \text{Traitement :} & \text{Pour }i \text{ allant de 1 à } n \text{ faire }\\ &\begin{array}{|l} d \text{ prend la valeur d'un entier aléatoire compris}\\ \text{entre 1 et }6\\ \text{ Si } d \leqslant 2\\ \hspace{0.5cm} \begin{array}{|l} \text{ alors } a \text{ prend la valeur } 1 - a\\ \text{ sinon Si } d \leqslant 4\\ \hspace{1.5cm}\begin{array}{|l} \text{ alors } b \text{ prend la valeur } 1 - b\\ \text{ sinon } c \text{ prend la valeur } 1 - c \end{array}\\ \hspace{1cm}\text{ FinSi }\\ \end{array}\\ \text{ FinSi }\\ s \text{ prend la valeur } a + b + c\\ \end{array}\\ &\text{ FinPour }\\ \text{Sortie :}&\text{ Afficher }s\\ \hline \end{array}$$
   1. On exécute cet algorithme en saisissant $n = 3$ et en supposant que les valeurs aléatoires générées successivement pour $d$ sont 1 ; 4 et 2. Recopier et compléter le tableau donné ci-dessous contenant l'état des variables au cours de l'exécution de l'algorithme :
      $$\begin{array}{|l|c|c|c|c|c|c|} \hline \text{variables}&i&d&a&b&c&s\\ \hline \text{initialisation}&\text{X}&\text{X}& & & &\text{X}\\ \hline 1^{er}\text{ passage boucle Pour}& & & & & & \\ \hline 2^{ e}\text{ passage boucle Pour}& & & & & & \\ \hline 3^{ e}\text{ passage boucle Pour}& &&&&&\\ \hline \end{array}$$
   2. Cet algorithme permet-il de savoir si, après une exécution de $n$ tirages, les trois pièces sont du côté pile ?
2. Pour tout entier naturel $n$, on note :
   $\bullet~~$ $X_n$ l'évènement: « À l'issue de $n$ lancers de dés, les trois pièces sont du côté face »
   $\bullet~~$ $Y_n$ l'évènement: « À l'issue de $n$ lancers de dés, une seule pièce est du côté pile et les autres sont du côté face»
   $\bullet~~$ $Z_n$ l'évènement: « À l'issue de $n$ lancers de dés, exactement deux pièces sont du côté pile et l'autre est du côté face»
   $\bullet~~$ $T_n$ l'évènement: « À l'issue de $n$ lancers de dés, les trois pièces sont du côté pile ».
   De plus on note, $x_n = p\left(X_n\right)$ ; $y_n = p\left(Y_n\right)$ ; $z_n = p\left(Z_n\right)$ et $t_n = p\left(T_n\right)$ les probabilités respectives des évènements $X_n$, $Y_n$, $Z_n$ et $T_n$.
   1. Donner les probabilités $x_0$ ,$y_0$, $z_0$ et $t_0$ respectives qu'au début du jeu il y ait 0, 1, 2 ou 3 pièces du côté pile.
   2. Recopier l'arbre ci-dessous et compléter les probabilités sur ses branches :
      
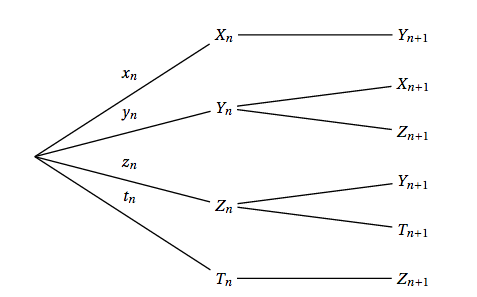
3. Pour tout entier naturel $n$, on note $U_n$ la matrice ligne $\left(x_n y_n z_n t_n\right)$.
   1. Donner la matrice $U_0$.
   2. À l'aide de l'arbre précédemment rempli, déterminer la matrice carrée $M$ telle que, pour tout entier naturel $n$, $U_{n+1} = U_n \times M$.
4. Démontrer que, pour tout entier naturel $n$, $U_n = U_0 \times M^n$.
5. On admet que, pour tout entier $n \geqslant 1$,
   $$\left\lbrace \begin{array}{l} x_n = \dfrac{(- 1)^n + 3 \times \left(- \frac{1}{3}\right)^n + 3\times \left(\frac{1}{3}\right)^n + 1}{8}~\\ y_n = \dfrac{- 3 \times \left(- \frac{1}{3}\right)^n + 3 \times \left(\frac{1}{3}\right)^n - (- 1)^n \times 3 + 3}{8}\\ z_n = \dfrac{- 3 \times \left(- \frac{1}{3}\right)^n - 3 \times \left(\frac{1}{3}\right)^n + (- 1)^n\times 3 + 3}{8}\\ t_n = \dfrac{- (- 1)^n + 3 \times \left(- \frac{1}{3}\right)^n - 3\times \left(\frac{1}{3}\right)^n + 1}{8} \end{array} \right. $$
   1. Calculer la probabilité, arrondie à $10^{-3}$ près, qu'au bout de 5 lancers de dés, une seule des trois pièces soit du côté pile.
   2. Préciser si les affirmations suivantes sont vraies ou fausses. Une réponse non justifiée n'est pas prise en compte.
      $\bullet~~$ Première affirmation : « À l'issue d'un nombre pair de lancers de dés, les pièces peuvent être toutes les trois du côté pile ».
      $\bullet~~$ Deuxième affirmation: « Au cours du jeu, la probabilité que les pièces soient toutes les trois du côté pile peut être supérieure ou égale à $\dfrac{1}{4}$ ».
      $\bullet~~$ Troisième affirmation: « Au cours du jeu, la probabilité que les pièces soient toutes les trois du côté pile peut être supérieure ou égale à $0,249$ ».

Correction de l'exercice de Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

On dispose d'un dé équilibré à 6 faces numérotées de 1 à 6 et de 3 pièces A, B et C ayant chacune un côté pile et un côté face. Un jeu consiste à lancer une ou plusieurs fois le dé. Après chaque lancer de dé, si l'on obtient 1 ou 2, alors on retourne la pièce A, si l'on obtient 3 ou 4, alors on retourne la pièce B et si l'on obtient 5 ou 6, alors on retourne la pièce C. Au début du jeu, les 3 pièces sont toutes du côté face.

1. Dans l'algorithme ci-dessous, 0 code le côté face et 1 code le côté pile. Si $a$ code un côté de la pièce A, alors $1 - a$ code l'autre côté de la pièce A. $$\begin{array}{|ll|}\hline \text{Variables :} &a, b, c, d, s\text{ sont des entiers naturels}\\ &i, n \text{ sont des entiers supérieurs ou égaux à } 1\\ \text{Initialisation :}&a \text{ prend la valeur }0\\ &b\text{ prend la valeur }0\\ &c \text{ prend la valeur }0\\ &\text{Saisir }n\\ \text{Traitement :} & \text{Pour }i \text{ allant de 1 à } n \text{ faire }\\ &\begin{array}{|l} d \text{ prend la valeur d'un entier aléatoire compris}\\ \text{entre 1 et }6\\ \text{ Si } d \leqslant 2\\ \hspace{0.5cm} \begin{array}{|l} \text{ alors } a \text{ prend la valeur } 1 - a\\ \text{ sinon Si } d \leqslant 4\\ \hspace{1.5cm}\begin{array}{|l} \text{ alors } b \text{ prend la valeur } 1 - b\\ \text{ sinon } c \text{ prend la valeur } 1 - c \end{array}\\ \hspace{1cm}\text{ FinSi }\\ \end{array}\\ \text{ FinSi }\\ s \text{ prend la valeur } a + b + c\\ \end{array}\\ &\text{ FinPour }\\ \text{Sortie :}&\text{ Afficher }s\\ \hline \end{array}$$
   1. On exécute cet algorithme en saisissant $n = 3$ et en supposant que les valeurs aléatoires générées successivement pour $d$ sont 1 ; 4 et 2. Recopier et compléter le tableau donné ci-dessous contenant l'état des variables au cours de l'exécution de l'algorithme :
      $$\begin{array}{|l|c|c|c|c|c|c|} \hline \text{variables}&i&d&a&b&c&s\\ \hline \text{initialisation}&\text{X}&\text{X}& & & &\text{X}\\ \hline 1^{er}\text{ passage boucle Pour}& & & & & & \\ \hline 2^{ e}\text{ passage boucle Pour}& & & & & & \\ \hline 3^{ e}\text{ passage boucle Pour}& &&&&&\\ \hline \end{array}$$
   $$\begin{array}{|l|c|c|c|c|c|c|} \hline \text{variables}&i&d&a&b&c&s\\ \hline \text{initialisation}&\text{X}&\text{X}&0&0&0&\text{X}\\ \hline 1^{er}\text{ passage boucle Pour}&1&1&1&0&0&1\\ \hline 2^{ e}\text{ passage boucle Pour}&2&4&1&1&0&2\\ \hline 3^{ e}\text{ passage boucle Pour}&3&2&0&1&0&1\\ \hline \end{array}$$
   2. Cet algorithme permet-il de savoir si, après une exécution de $n$ tirages, les trois pièces sont du côté pile ?
   A chaque étape la variable $s$ détermine le nombre de pièces se trouvant du côté pile.
   L’algorithme permet donc de dite si, après $n$ tirages, les trois pièces sont du côté pile.
   $\quad$
2. Pour tout entier naturel $n$, on note :
   $\bullet~~$ $X_n$ l'évènement: « À l'issue de $n$ lancers de dés, les trois pièces sont du côté face »
   $\bullet~~$ $Y_n$ l'évènement: « À l'issue de $n$ lancers de dés, une seule pièce est du côté pile et les autres sont du côté face»
   $\bullet~~$ $Z_n$ l'évènement: « À l'issue de $n$ lancers de dés, exactement deux pièces sont du côté pile et l'autre est du côté face»
   $\bullet~~$ $T_n$ l'évènement: « À l'issue de $n$ lancers de dés, les trois pièces sont du côté pile ».
   De plus on note, $x_n = p\left(X_n\right)$ ; $y_n = p\left(Y_n\right)$ ; $z_n = p\left(Z_n\right)$ et $t_n = p\left(T_n\right)$ les probabilités respectives des évènements $X_n$, $Y_n$, $Z_n$ et $T_n$.
   1. Donner les probabilités $x_0$ ,$y_0$, $z_0$ et $t_0$ respectives qu'au début du jeu il y ait 0, 1, 2 ou 3 pièces du côté pile.
   Au début du jeu, toutes les pièces sont du côté face.
   Donc $p\left(X_0\right)=1$, $p\left(Y_0\right)=0$, $p\left(Z_0\right)=0$ et $p\left(T_0\right)=0$.
   $\quad$
   
   2. Recopier l'arbre ci-dessous et compléter les probabilités sur ses branches :
      
   
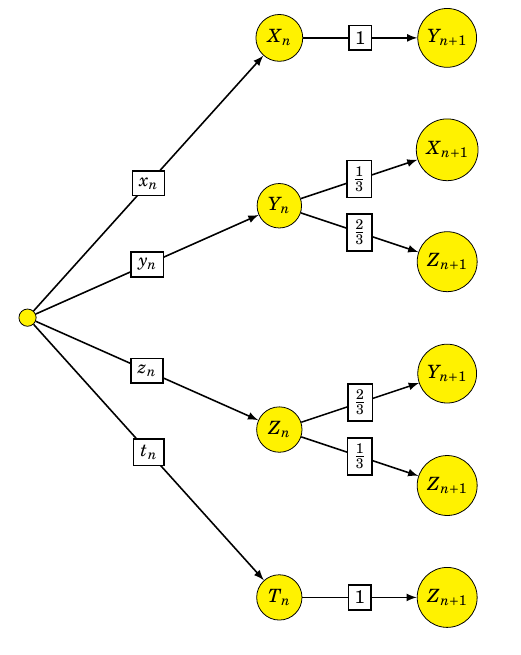
3. Pour tout entier naturel $n$, on note $U_n$ la matrice ligne $\left(x_n y_n z_n t_n\right)$.
   1. Donner la matrice $U_0$.
   On a $U_0=\begin{pmatrix}1&0&0&0\end{pmatrix}$
   
   2. À l'aide de l'arbre précédemment rempli, déterminer la matrice carrée $M$ telle que, pour tout entier naturel $n$, $U_{n+1} = U_n \times M$.
   On a $M=\begin{pmatrix}0&\dfrac{1}{3}&0&0\\1&0&\dfrac{2}{3}&0\\0&\dfrac{2}{3}&\dfrac{1}{3}&1\\0&0&0&1 \end{pmatrix}$
   $\quad$
4. Démontrer que, pour tout entier naturel $n$, $U_n = U_0 \times M^n$.
Montrons par récurrence que, pour tout entier naturel $n$ on a $U_{n+1}=U_0\times M^n$
Initialisation : Si $n=0$ alors $U_0\times M^0=U_0\times I_4=U_0$ où $I_4$ est la matrice identité.
La propriété est donc vraie au rang $0$.
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$ : $U_n=U_0\times M^n$
$\begin{align*} U_{n+1}&=U_n\times M \\ &=U_0\times M^n\times M \\ &=U_0\times M^{n+1}
\end{align*}$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Donc pour tout entier naturel $n$ on a $U_n=U_0 \times M^n$.
$\quad$
5. On admet que, pour tout entier $n \geqslant 1$,
   $$\left\lbrace \begin{array}{l} x_n = \dfrac{(- 1)^n + 3 \times \left(- \frac{1}{3}\right)^n + 3\times \left(\frac{1}{3}\right)^n + 1}{8}~\\ y_n = \dfrac{- 3 \times \left(- \frac{1}{3}\right)^n + 3 \times \left(\frac{1}{3}\right)^n - (- 1)^n \times 3 + 3}{8}\\ z_n = \dfrac{- 3 \times \left(- \frac{1}{3}\right)^n - 3 \times \left(\frac{1}{3}\right)^n + (- 1)^n\times 3 + 3}{8}\\ t_n = \dfrac{- (- 1)^n + 3 \times \left(- \frac{1}{3}\right)^n - 3\times \left(\frac{1}{3}\right)^n + 1}{8} \end{array} \right. $$
   1. Calculer la probabilité, arrondie à $10^{-3}$ près, qu'au bout de 5 lancers de dés, une seule des trois pièces soit du côté pile.
   On veut calculer $y_5=\dfrac{-3\times \left(-\dfrac{1}{3}\right)^5+3\times \left(\dfrac{1}{3}\right)^5-(-1)^5\times 3+3}{8}$
   Soit $y_5 \approx 0,753$.
   $\quad$
   
   2. Préciser si les affirmations suivantes sont vraies ou fausses. Une réponse non justifiée n'est pas prise en compte.
      $\bullet~~$ Première affirmation : « À l'issue d'un nombre pair de lancers de dés, les pièces peuvent être toutes les trois du côté pile ».
      $\bullet~~$ Deuxième affirmation: « Au cours du jeu, la probabilité que les pièces soient toutes les trois du côté pile peut être supérieure ou égale à $\dfrac{1}{4}$ ».
      $\bullet~~$ Troisième affirmation: « Au cours du jeu, la probabilité que les pièces soient toutes les trois du côté pile peut être supérieure ou égale à $0,249$ ».
   Première affirmation : fausse
   Si $n$ est pair alors $(-1)^n=1$ et $\left(-\dfrac{1}{3}\right)^n=\dfrac{1}{3^n}$
   Donc $t_n=\dfrac{-1+\dfrac{3}{3^n}-\dfrac{3}{3^n}+1}{8}=0$
   $\quad$
   Deuxième affirmation : fausse
   On a vu que si $n$ est pair alors $t_n=0$
   Si $n$ est impair alors $(-1)^n=-1$ et $\left(-\dfrac{1}{3}\right)^n=-\dfrac{1}{3^n}$
   Donc $t_n=\dfrac{1-\dfrac{3}{3^n}-\dfrac{3}{3^n}+1}{8}=\dfrac{1-\dfrac{1}{3^{n-1}}}{4}<4$ si $n\geq 1$
   $\quad$
   Troisième affirmation : vraie
   $u_7\approx 0,249~66 >0,249 $
   $\quad$