Puissance 11 2014 Concours FEISIC
Calculatrice interdite ; traiter $12$ exercices sur les $16$ en $2$ h $30$ ; répondre par Vrai ou Faux sans justification. $+ 1$ si bonne réponse, $-1$ si mauvaise réponse, $0$ si pas de réponse, bonus d'un point pour un exercice entièrement juste.
Exercice 1 : Bases en Analyse
Les questions sont indépendantes.
- Soit $x \in \mathbb R$, la dérivée de $x \longmapsto \dfrac{x}{\text{e}^x}$ est $x \longmapsto \dfrac{x - 1}{\text{e}^x}$.
- $\displaystyle\lim_{x \to + \infty} = \dfrac{x}{\text{e}^x} = + \infty$. Soit $f$ une fonction définie sur $]0~;~+ \infty[$ telle que, pour tout $x > 0 : \: \dfrac{1}{x} \leqslant f(x) \leqslant \dfrac{x}{\text{e}^x}$.
- $\displaystyle\lim_{x \to + \infty} f(x) = 0$. Soit $\left(u_{n}\right)$ la suite définie, pour tout entier naturel $n$ non nul, par $u_{n} = \ln \left(\dfrac{1}{n}\right)$.
- La suite $\left(u_{n}\right)$ converge vers $0$.
Exercice 2 : Bases en Géométrie
Les questions sont indépendantes. Soit $(P)$ et $(Q)$ les plans d'équations respectives \[(P) :\: 2x + y + z = 2 \quad \text{et} \quad (Q) : x + y - z = 0.\]
- L'intersection des plans $(P)$ et $(Q)$ a pour équation $x + 2z = 2$. Soit $(D)$ la droite dont une représentation paramétrique est $\left\{\begin{array}{l c l} x&=&t+3\\ y&=& - t - 1\\ z&=&2 \end{array}\right. \text{avec}\: t \in \mathbb R.$
- $(D)$ est perpendiculaire au plan $(R)$ d'équation $x - y + 2z = 0$.
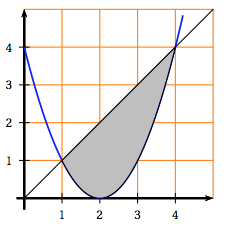
- Sur le graphique ci-dessous, nous avons tracé les courbes représentatives des fonctions $f$ : $x \longmapsto x$ et $g$ : $x \longmapsto (x - 2)^2$. L'aire $A$ du domaine hachuré est égale à $A = \dfrac{9}{2}$ unités d'aire.
- La courbe représentative de la fonction $f$ définie sur $]1~;~+ \infty[$ par $f(x) = \ln \left(\dfrac{2x^2 - x + 3}{x - 1}\right)$ admet une asymptote horizontale d'équation $y = \ln 2$.
Exercice 3 : Lecture graphique
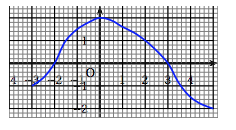
$f$ est une fonction définie et dérivable sur $[-3~;~5]$ de courbe représentative $(C)$. On donne ci-dessous la courbe $(\Gamma)$ représentative de sa fonction dérivée $f'$.
- $(C)$ admet une tangente horizontale en $x = 0$.
- $f$ admet un minimum relatif en $x = - 2$.
- La fonction $f$ est strictement décroissante sur [0 ; 5].
- Les tangentes à $(C)$ aux points d'abscisses $- \dfrac{3}{2}$ et $2$ sont parallèles.
Exercice 4 : Suite définie par un algorithme
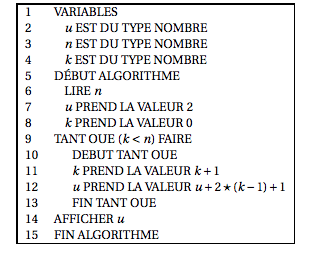
Soit $n \in \mathbb N$, on considère la suite $\left(u_{n}\right)$ où $u_{n}$ est le réel affiché par l'algorithme ci-dessous lorsque l'utilisateur entre la valeur de $n$.
- $u_{3} = 11$.
- Pour tout entier naturel $n,\: u_{n+1} = u_{n} + 2n + 1$.
- La suite $\left(u_{n}\right)$ est strictement croissante.
- Pour tout entier naturel $n$, $u_{n} = n^2 + 2.$
Exercice 5 : Bases sur les complexes
Le plan complexe est rapporté à un repère orthonormal direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. On considère les nombres complexes $z_{1} = \left(\sqrt{6} + \sqrt{2}\right) + \text{i}\left(\sqrt{6} - \sqrt{2}\right)$ et $z_{2} = \dfrac{1 + \text{i}}{\sqrt{3} + \text{i}}$.
- $z_{1}^2 = 8\sqrt{3} + 8\text{i}$.
- $\left|z_{2}\right| = \sqrt{2}$.
- $\text{arg}\left(z_{1}^2\right) = \dfrac{5\pi} {6} \quad [2\pi]$.
- $z_{2} = \dfrac{\sqrt{2}}{2}\times \text{e}^{\text{i}\frac{\pi}{2}}$.
Exercice 6 : Bases de logique
Le plan complexe est muni du repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. $x$ et $y$ sont deux nombres réels et $z$ est le nombre complexe $x + \text{i}y$.
- La négation de la proposition : « $x \geqslant 0$ et $y \geqslant 0$ » est la proposition « $x < 0$ et $y < 0 $ ».
- Si $x = y$ alors arg$(z) = \frac{\pi}{4}$ modulo $2\pi$.
- La réciproque de la proposition précédente est vraie.
- On suppose $z \neq 0$. Si $z = \dfrac{1}{z}$, alors $x = 0$ ou $y = 0$.
Exercice 7 : Calculs de limites
- La fonction $x \longmapsto x \times \sin (x)$ n'a pas de limite lorsque $x$ tend vers $+ \infty$.
- $\displaystyle\lim_{x \to + \infty} \dfrac{\cos (x) + 2}{\cos (x) + x}= 1$.
- $\displaystyle\lim_{x \to - \infty} \dfrac{\text{e}^x + 3x}{x + 1} = 0$.
- $\displaystyle\lim_{x \to 0} \dfrac{\ln (1 + x)}{x^2} = 1$.
Exercice 8 : Calculs d'intégrales
- $\displaystyle\int_{2}^4 \dfrac{3}{x^2}\:\text{d}x = \dfrac{5}{4}$. Soit $f$ la fonction définie sur $]0~;~+ \infty[$ par $f(x) = \dfrac{x + 1}{x^2 + 2x}$.
- La fonction $F$ définie sur $]0~;~+ \infty[$ par $F(x) = 1 + \dfrac{\ln \left(x^2 + 2x\right)}{2}$ est une primitive de $f$.
- $\displaystyle\int_{2}^{\text{e}} \dfrac{1 + t}{t^2}\:\text{d}t = 2 - \dfrac{1}{\text{e}}$.
- $\displaystyle\int_{0}^{1} \dfrac{\text{e}^x - x \text{e}^x}{\text{e}^{2x}} = \dfrac{1}{\text{e}}$.
Exercice 9 : Transformation complexe
Le plan complexe est rapporté à un repère orthonormal direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. Soit $f$ la transformation du plan complexe qui, à tout point $M$ d'affixe $z$, associe le point $M'$ d'affixe \[z' = (1 + \text{i})z + 1.\]
- L'image, par $f$, du point B d'affixe 2 est le point C d'affixe $3 + 2\text{i}$.
- Le point A d'affixe i est le seul point invariant par $f$.
- L'image, par $f$, de l'axe des réels est la droite (BC).
- Soit D le point d'affixe 1. Pour tout point $M$ distinct de A et de D, le triangle D$MM'$ est isocèle en $M$.
Exercice 10 : Loi normale
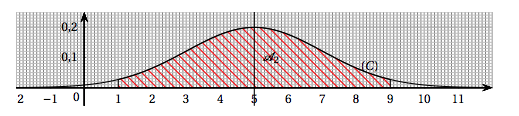
Dans tout l'exercice, on suppose $T$ une variable aléatoire qui suit la loi normale $\mathcal{N}\left(\mu,~\sigma^2\right)$ avec $\mu$ et $\sigma$ deux entiers naturels. La densité de probabilité de cette loi, notée $f$, est représentée ci-dessous par la courbe $(C)$. On suppose que $(C)$ admet la droite $x = 5$ comme axe de symétrie et que l'aire du domaine $\mathcal{A}_{1}$ (représenté en gris) est environ égale à $0,68$. 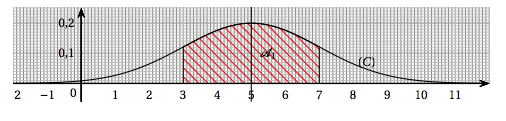
- $\mu = 5$ et $\sigma = 4$.
- L'aire du domaine $\mathcal{A}_{2}$, représenté ci-dessous, est environ égale à $0,8$.
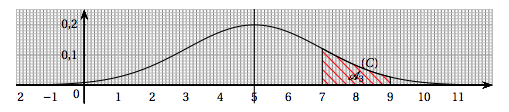
- L'aire du domaine $\mathcal{A}_{3}$ représenté ci-dessous, est environ égale à $0,135$.
- On admet, dans cette question, que $P(T \in [\mu - 2\sigma~;~\mu + 2\sigma]) \approx 0,95$.
$P(T \leqslant 9) \approx 0,975$.
Exercice 11 : Nombres complexes et géométrie
Le plan complexe est muni d'un repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. À chaque point $M$ d'affixe $z \neq 0$, on associe l'unique point $M'$ d'affixe $z'$ tel que, \[z' = \left(\dfrac{\overline{z}}{|z|}\right)^2.\]
- En posant $z = x + \text{i}y$,avec $x \neq 0$ ou $ y \neq 0$, et $z'= x'+ \text{i}y'$, on a : $x'= \dfrac{x^2 - y^2}{x^2 + y^2}$ et $y' = \dfrac{2xy}{x^2 + y^2}$.
- $M'$ appartient à l'axe des ordonnées si et seulement si $M$ appartient à la droite d'équation $y = x$ privée de O.
- $M'$ est un point du cercle trigonométrique.
- $M'$ a pour affixe $- 1$ si et seulement si $z = \text{i}$ ou $z = - \text{i}$.
Exercice 12 : Étude d'une fonction logarithme
On considère la fonction $f$ définie sur $\mathbb R$ par \[f(x) = \ln \left(x^2 + x + 1\right)\] de courbe représentative $(\mathcal{C})$.
- $f$ est croissante sur $\mathbb R$.
- $(\mathcal{C})$ admet une unique asymptote verticale.
- Pour tout $x \in \mathbb R,\: f(x) \geqslant \ln \left(\dfrac{3}{4}\right)$.
- Il existe deux points de $(\mathcal{C})$ ayant une tangente à $(\mathcal{C})$ parallèle à la droite $(\Delta)$ d'équation $y = x - \ln 7$.
Exercice 13 : Étude d'une fonction exponentielle
Soit $f$ la fonction définie sur $\mathbb R$ par $f(x) = \dfrac{1}{2}\text{e}^{2x} + \text{e}^{x} - 2x$. On désigne par $\left(C_f\right)$ sa représentation graphique dans un repère orthonormé du plan.
- Pour tout réel $x$, on a : $f'(x) = \left(\text{e}^{x} - 1\right)\left(\text{e}^{x} + 2\right)$.
- Pour tout réel $x$, on a : $f( x) > \dfrac{3}{2}$.
- $\left(C_f\right)$ admet l'axe des abscisses comme asymptote horizontale en $+ \infty$.
- $\displaystyle\lim_{x \to - \infty} f(x) = + \infty$.
Exercice 14 : Probabilités conditionnelles
Un joueur effectue des parties successives d'un jeu vidéo.
- La probabilité qu'il gagne la première partie est de $0,2$.
- S'il gagne une partie, la probabilité de gagner la suivante est égale à $0,7$.
- S'il perd une partie, la probabilité de gagner la suivante est égale à $0,5$.
Pour tout entier naturel $n$ non nul, on note :
- $G_{n}$ l'évènement : « le joueur gagne la $n$-ième partie » ;
- $p_{n}$ la probabilité de l'évènement $G_{n}$.
- $p_{2} = 0,54$.
- Le joueur gagne la deuxième partie. La probabilité qu'il ait perdu la première est $0,6$.
- Pour tout entier naturel $n$ non nul, on a $p_{n+1} = \dfrac{1}{5}p_{n} + \dfrac{1}{2}$. Pour le d. , on donne l'algorithme ci-dessous :
- Si on teste le programme pour $n = 5$ alors cet algorithme restitue la probabilité que le joueur gagne la cinquième partie.

Exercice 15 : Différentes lois de probabilités
Les quatre questions sont indépendantes.
- Soit $t > 0$. Si $X$ suit une loi uniforme sur $[0~;~t]$ telle que $p(X < 5) = 0,4$ alors $t = 20$.
- Soit $n \in \mathbb N*$. Si $X$ suit une loi binomiale $\mathcal{B}(n~;~0,3)$ d'espérance $12$, alors $n = 40$.
- Si $X$ suit une loi exponentielle de paramètre $\lambda = 2 \times 10^{-3}$, alors $\text{E}(X) = 5000$.
- On considère $A$ et $B$ deux évènements d'une même expérience aléatoire tels que $p(A) \neq 0$ et $p(B) \neq 0$. Si $P_{B}(A) = P_{A}(B)$, alors $p(A)= p(B)$.
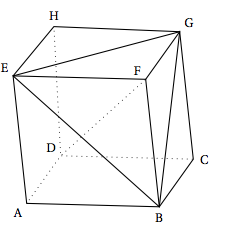
Exercice 16 : Repérage dans un cube
Dans le cube ABCDEFGH, d'arête de longueur 1, on considère le repère orthonormé $\left(\text{A}~;~\vec{\text{AB}},~ \vec{\text{AD}},~ \vec{\text{AE}}\right)$.
On rappelle que :
- Le plan médiateur d'un segment est le plan passant par le milieu de ce segment tout en lui étant perpendiculaire.
- Si $M$ est un point de l'espace et (P) un plan de l'espace, on appelle distance du point $M$ au plan (P) la plus petite distance $d$ entre le point $M$ et un point $H$ du plan (P).
- (GDF) est le plan médiateur du segment [EB].
- Le plan (BEG) a pour équation : $x - y + z = 1$.
- I$\left(\dfrac{2}{3}~;~\dfrac{1}{3}~;~\dfrac{2}{3}\right)$ est le point d'intersection de la droite (DF) avec le plan (BEG).
- La distance du point D au plan (BEG) est égale à $\dfrac{\sqrt{3}}{3}$.
- Vues: 5804