Baccalauréat S Liban 27 mai 2015
Exercice 1 6 points
ABCDEFGH est un cube. 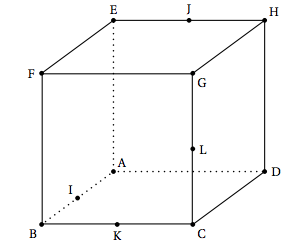
I est le milieu du segment [AB], J est le milieu du segment [EH], K est le milieu du segment [BC] et L est le milieu du segment [CG]. On munit l'espace du repère orthonormé $\left(\text{A}~;~\vec{\text{AB}},~ \vec{\text{AD}},~ \vec{\text{AE}}\right)$.
-
- Démontrer que la droite (FD) est orthogonale au plan (IJK).
- En déduire une équation cartésienne du plan (IJK).
- Déterminer une représentation paramétrique de la droite (FD).
- Soit $M$ le point d'intersection de la droite (FD) et du plan (IJK). Déterminer les coordonnées du point $M$.
- Déterminer la nature du triangle IJK et calculer son aire.
- Calculer le volume du tétraèdre FIJK.
- Les droites (IJ) et (KL) sont-elles sécantes ?
Correction de l'exercice 1 (5 points)
ABCDEFGH est un cube. 
I est le milieu du segment [AB], J est le milieu du segment [EH], K est le milieu du segment [BC] et L est le milieu du segment [CG]. On munit l'espace du repère orthonormé $\left(\text{A}~;~\vec{\text{AB}},~ \vec{\text{AD}},~ \vec{\text{AE}}\right)$.
-
- Démontrer que la droite (FD) est orthogonale au plan (IJK). Déterminons tout d’abord les coordonnées de quelques points :
- En déduire une équation cartésienne du plan (IJK). Une équation du plan $(IJK)$ est donc de la forme :
$I(0,5;0;0)$, $J(0;0,5;1)$, $K(1;0,5;0)$, $F(1;0;1)$ et $D(0;1;0)$
Ainsi $\vec{IJ}(-0,5;0,5;1)$, $\vec{IK}(0,5;0,5;0)$ et $\vec{DF}(1;-1;1)$.
Les vecteurs $\vec{IJ}$ et $\vec{IK}$ ne sont clairement pas colinéaires. Ils définissent donc bien le plan $(IJK)$.
$\vec{DF}.\vec{IJ} = -0,5 \times 1 + 0,5 \times (-1) + 1 \times 1 = 0$.
$\vec{DF}.\vec{IK} = 0,5 \times 1 + 0,5 \times (-1) + 0 \times 1 = 0$.
Ainsi le vecteur $\vec{DF}$ est orthogonal à deux vecteurs non colinéaires du plan $(IJK)$. C’est donc un vecteur normal de ce plan.
La droite $(DF)$ est bien orthogonale au plan $(IJK)$.
$\quad$
$$x-y+z+d=0$$
Le point $I(0,5;0;0)$ appartient au plan donc
$$0,5 + d =0 \iff d=-0,5$$
Une équation du plan $(IJK)$ est donc :
$$x-y+z-0,5 = 0$$ - Déterminer une représentation paramétrique de la droite (FD). En utilisant le point $F$ et le vecteur $\vec{DF}$ ont obtient la représentation paramétrique suivante de la droite $(DF)$ :
- Soit $M$ le point d'intersection de la droite (FD) et du plan (IJK). Déterminer les coordonnées du point $M$. Les coordonnées du point $M$ vérifient à la fois les équations de $(DF)$ et l’équation de $(IJK)$.
- Déterminer la nature du triangle IJK et calculer son aire. $IJ = \sqrt{(-0,5)^2+0,5^2+1^2} = \sqrt{1,5}$
- Calculer le volume du tétraèdre FIJK. $[MF]$ est la hauteur issue de $F$ du tétraèdre $FIJK$.
- Les droites (IJ) et (KL) sont-elles sécantes ?
- Calculer $u_0 = \displaystyle\int_0^1 \dfrac{1}{1 + x} \:\text{d}x$.
-
- Démontrer que, pour tout entier naturel $n$, $u_{n+1} + u_n = \dfrac{1}{n + 1}$.
- En déduire la valeur exacte de $u_1$.
-
- Recopier et compléter l'algorithme ci-dessous afin qu'il affiche en sortie le terme de rang $n$ de la suite $\left(u_n\right)$ où $n$ est un entier naturel saisi en entrée par l'utilisateur. $$ \begin {array}{|cc|}\hline \text{Variables :}& i \text{ et } n \text{ sont des entiers naturels}\\ & u \text{ est un réel}\\ \text{Entrée :}& \text{Saisir } n \\ \text{Initialisation :}& \text{Affecter à } u \text{ la valeur } \ldots\\ \text{Traitement :}& \text{ Pour } i \text{ variant de 1 à } \ldots\\ &\hspace{0.4cm} | \text{ Affecter à } u \text{ la valeur }\ldots\\ & \text{Fin de Pour }\\ \text{ Sortie :}& \text{ Afficher } u \\ \hline \end {array} $$
- À l'aide de cet algorithme, on a obtenu le tableau de valeurs suivant : $$\begin {array}{ |c|c| c|c|c|c| c|c|c|}\hline n & 0 &1 &2 &3 &4 &5 &10 &50 &100\\ \hline u_n & 0,6931 & 0,3069 & 0,1931 & 0,1402 & 0,1098 & 0,0902 & 0,0475 & 0,0099 & 0,0050 \\ \hline \end {array}$$ Quelles conjectures concernant le comportement de la suite $\left(u_n\right)$ peut-on émettre ?
-
- Démontrer que la suite $\left(u_n\right)$ est décroissante.
- Démontrer que la suite $\left(u_n\right)$ est convergente.
- On appelle $\ell$ la limite de la suite $\left(u_n\right)$. Démontrer que $\ell = 0$.
- Calculer $u_0 = \displaystyle\int_0^1 \dfrac{1}{1 + x} \:\text{d}x$. $\begin{align*} u_0 &=\displaystyle \int_0^1 \dfrac{1}{1+x}\mathrm{d}x\\ &= \left[\ln(1+x)\right]_0^1\\ &=\ln 2 – \ln 1\\ &=\ln 2 \end{align*}$
-
- Démontrer que, pour tout entier naturel $n$, $u_{n+1} + u_n = \dfrac{1}{n + 1}$. $\begin{align*} u_{n+1}+u_n &= \displaystyle \int_0^1 \dfrac{x^{n+1}}{1+x} \mathrm{d}x + \int_0^1 \dfrac{x^n}{1+x}\mathrm{d}x\\ &= \int_0^1 \dfrac{x^{n+1}+x^n}{1+x}\mathrm{d}x\\ &=\int_0^1 \dfrac{x^n(1+x)}{1+x}\mathrm{d}x\\ &=\int_0^1 x^n \mathrm{d}x\\ &=\left[\dfrac{x^{n+1}}{n+1}\right]_0^1\\ &=\dfrac{1}{n+1}
- En déduire la valeur exacte de $u_1$. On a ainsi $u_1+u_0 = 1 \iff u_1 = 1 – \ln 2$
\end{align*}$
-
- Recopier et compléter l'algorithme ci-dessous afin qu'il affiche en sortie le terme de rang $n$ de la suite $\left(u_n\right)$ où $n$ est un entier naturel saisi en entrée par l'utilisateur. $$ \begin {array}{|cc|}\hline \text{Variables :}& i \text{ et } n \text{ sont des entiers naturels}\\ & u \text{ est un réel}\\ \text{Entrée :}& \text{Saisir } n \\ \text{Initialisation :}& \text{Affecter à } u \text{ la valeur } \ldots\\ \text{Traitement :}& \text{ Pour } i \text{ variant de 1 à } \ldots\\ &\hspace{0.4cm} | \text{ Affecter à } u \text{ la valeur }\ldots\\ & \text{Fin de Pour }\\ \text{ Sortie :}& \text{ Afficher } u \\ \hline \end {array} $$ $\quad$
- À l'aide de cet algorithme, on a obtenu le tableau de valeurs suivant : $$\begin {array}{ |c|c| c|c|c|c| c|c|c|}\hline n & 0 &1 &2 &3 &4 &5 &10 &50 &100\\ \hline u_n & 0,6931 & 0,3069 & 0,1931 & 0,1402 & 0,1098 & 0,0902 & 0,0475 & 0,0099 & 0,0050 \\ \hline \end {array}$$ Quelles conjectures concernant le comportement de la suite $\left(u_n\right)$ peut-on émettre ? La suite $(u_n)$ semble être décroissante et converger vers $0$.
Variables :
$\quad$ $i$ et $n$ sont des entiers naturels
$\quad$ $u$ est un réel
Entrée :
$\quad$ Saisir $n$
Initialisation :
$\quad$ Affecter à $u$ la valeur $\ln 2$
Traitement :
$\quad$ Pour $i$ variant de $1$ à $n$
$\qquad$ Affecter à $u$ la valeur $\dfrac{1}{i} – u$
$\quad$ Fin de Pour
Sortie :
$\quad$ Afficher $u$
$\quad$
-
- Démontrer que la suite $\left(u_n\right)$ est décroissante. $\begin{align*} u_{n+1}-u_n &= \displaystyle \int_0^1 \dfrac{x^{n+1}}{1+x}\mathrm{d}x – \int_0^1 \dfrac{x^n}{1+x}\mathrm{d}x\\ &= \int_0^1 \dfrac{x^n(x-1)}{1+x} \mathrm{d}x \end{align*}$
- Démontrer que la suite $\left(u_n\right)$ est convergente. La fonction définie sur $[0;1]$ par $x \mapsto \dfrac{x^n}{1+x}$ est continue et positive pour tout $n$.
Or sur $[0;1]$, $x^n \ge 0$, $1+x > 0$ et $x-1 \le 0$
Donc $\displaystyle \int_0^1 \dfrac{x^n(x-1)}{1+x}\mathrm{d}x \le 0$ (puisque la fonction qu’on intègre est continue sur $[0;1]$).
Ainsi la suite $(u_n)$ est décroissante.
Ainsi, pour tout entier naturel $n$, $u_n \ge 0$.
La suite $(u_n)$ est décroissante et minorée par $0$. Elle converge donc. - On appelle $\ell$ la limite de la suite $\left(u_n\right)$. Démontrer que $\ell = 0$. On a, pour tout entier naturel $n$, $u_{n+1}+u_n = \dfrac{1}{n+1}\; (1)$.
- Dans cette question, on choisit $m = \text{e}$. Démontrer que la droite $\mathcal{D}_{\text{e}}$, d'équation $y = \text{e}x$, est tangente à la courbe $\mathcal{C}$ en son point d'abscisse 1.
- Conjecturer, selon les valeurs prises par le réel strictement positif $m$, le nombre de points d'intersection de la courbe $\mathcal{C}$ et de la droite $\mathcal{D}_m$.
- Démontrer cette conjecture.
- Dans cette question, on choisit $m = \text{e}$. Démontrer que la droite $\mathcal{D}_{\text{e}}$, d'équation $y = \text{e}x$, est tangente à la courbe $\mathcal{C}$ en son point d'abscisse 1. La fonction exponentielle est dérivable sur $\mathbb R$ de dérivée elle-même.
- Conjecturer, selon les valeurs prises par le réel strictement positif $m$, le nombre de points d'intersection de la courbe $\mathcal{C}$ et de la droite $\mathcal{D}_m$. On peut conjecturer que :
- Démontrer cette conjecture. On appelle $f_m$ la fonction définie sur $\mathbb R$ par $f_m(x)= \text{e}^x-mx$
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = \left]\2 ; \3\right]$.
- $\1$ est strictement décroissante sur l' intervalle $I = \left]\2 ; \3\right]$.
- $\lim\limits_{x \to \2}~\1(x)=\4$ et $\1 \left(\3\right)=\5$
- $\1 $ est une fonction dérivable donc continue sur l' intervalle $I = \left[\2 ; \3\right[$.
- $\1$ est strictement croissante sur l' intervalle $I = \left[\2 ; \3\right[$.
- $\1 \left(\2\right)=\4$ et $\lim\limits_{x \to \3}~\1(x)=\5$
- $A$ l'évènement « La personne interrogée affirme vouloir voter pour le candidat A » ;
- $B$ l'évènement « La personne interrogée affirme vouloir voter pour le candidat B » ;
- $V$ l'évènement « La personne interrogée dit la vérité ».
- Construire un arbre de probabilités traduisant la situation.
-
- Calculer la probabilité que la personne interrogée dise la vérité.
- Démontrer que la probabilité que la personne choisie vote effectivement pour le candidat A est $0,529$.
- L'institut de sondage publie alors les résultats suivants : $$ \begin {array}{|c|}\hline \text{52,9% des électeurs* voteraient pour le candidat A.}\\ \text{* estimation après redressement, fondée sur un sondage d'un échantillon représentatif de 1200 personnes.}\\ \hline \end {array} $$ Au seuil de confiance de 95%, le candidat A peut- il croire en sa victoire ?
- Pour effectuer ce sondage, l'institut a réalisé une enquête téléphonique à raison de 10 communications par demi-heure. La probabilité qu'une personne contactée accepte de répondre à cette enquête est $0,4$. L'institut de sondage souhaite obtenir un échantillon de 1200 réponses. Quel temps moyen, exprimé en heures, l'institut doit-il prévoir pour parvenir à cet objectif ?
- $A$ l'évènement « La personne interrogée affirme vouloir voter pour le candidat A » ;
- $B$ l'évènement « La personne interrogée affirme vouloir voter pour le candidat B » ;
- $V$ l'évènement « La personne interrogée dit la vérité ».
- Construire un arbre de probabilités traduisant la situation.
-
- Calculer la probabilité que la personne interrogée dise la vérité. D’après la formule des probabilités totales on a :
- Sachant que la personne interrogée dit la vérité, calculer la probabilité qu'elle affirme vouloir voter pour le candidat A. $p_V(A) = \dfrac{p(V \cap A)}{p(V)} = \dfrac{0,47 \times 0,9}{0,847}$ $=\dfrac{423}{847}$
$$\begin{align*} p(V) &= p(A\cap V)+p(B\cap V)\\& =0,47 \times 0,9 + 0,53 \times 0,8\\ & = 0,847 \end{align*}$$
$\quad$ - Démontrer que la probabilité que la personne choisie vote effectivement pour le candidat A est $0,529$. La probabilité que la personne choisie vote effectivement pour le candidat A est donnée par :
- L'institut de sondage publie alors les résultats suivants : $$ \begin {array}{|c|}\hline \text{52,9% des électeurs* voteraient pour le candidat A.}\\ \text{* estimation après redressement, fondée sur un sondage d'un échantillon représentatif de 1200 personnes.}\\ \hline \end {array} $$ Au seuil de confiance de 95%, le candidat A peut- il croire en sa victoire ? On a $n= 1~200 > 30$ et $f=0,529$
- Pour effectuer ce sondage, l'institut a réalisé une enquête téléphonique à raison de 10 communications par demi-heure. La probabilité qu'une personne contactée accepte de répondre à cette enquête est $0,4$. L'institut de sondage souhaite obtenir un échantillon de 1200 réponses. Quel temps moyen, exprimé en heures, l'institut doit-il prévoir pour parvenir à cet objectif ? Soit $n$ le nombre de demi-heures nécessaires à cette enquête.
- s'il ne fume pas un jour donné, il ne fume pas le jour suivant avec une probabilité de 0,9 ;
- s'il fume un jour donné, il fume le jour suivant avec une probabilité de 0,6.
- Calculer $p_1$ et $q_1$.
- On utilise un tableur pour automatiser le calcul des termes successifs des suites $\left(p_n\right)$ et $\left(q_n\right)$. Une copie d'écran de cette feuille de calcul est fournie ci-dessous : $$ \begin {array}{|c|c|c|c|c|}\hline &A &B &C &D\\ \hline 1 &n &p_n &q_n &\\ \hline 2 &0 &0 &1 &\\ \hline 3 &1 & & &\\ \hline 4 &2 & & &\\ \hline 5 &3 & & &\\ \hline \end {array} $$ Dans la colonne A figurent les valeurs de l'entier naturel $n$. Quelles formules peut-on écrire dans les cellules B3 et C3 de façon qu'en les recopiant vers le bas, on obtienne respectivement dans les colonnes B et C les termes successifs des suites $\left(p_n\right)$ et $\left(q_n\right)$ ?
- On définit les matrices $M$ et, pour tout entier naturel $n$, $X_n$ par $$M = \begin{pmatrix}0,9& 0,4\\0,1& 0,6\end{pmatrix}\quad \text{et}\quad X_n = \begin{pmatrix}p_n\\q_n \end{pmatrix}.$$ On admet que $X_{n+1} = M \times X_n$ et que, pour tout entier naturel $n$,\: $X_n = M^n \times X_0$. On définit les matrices $A$ et $B$ par $A = \begin{pmatrix}0,8&0,8\\0,2&0,2\end{pmatrix}$ et $B = \begin{pmatrix}0,2& - 0,8\\- 0,2&0,8\end{pmatrix}$.
- Démontrer que $M = A + 0,5B$.
- Vérifier que $A^2 = A$, et que $A \times B = B \times A = \begin{pmatrix}0& 0\\0& 0\end{pmatrix}$. On admet dans la suite que, pour tout entier naturel $n$ strictement positif, $A^n = A$ et $B^n = B$.
- Démontrer que, pour tout entier naturel $n$, $M^n = A + 0,5^n B$.
- En déduire que, pour tout entier naturel $n$ $p_n = 0,8 - 0,8 \times 0,5^n$.
- À long terme, peut-on affirmer avec certitude que le fumeur arrêtera de fumer ?
- s'il ne fume pas un jour donné, il ne fume pas le jour suivant avec une probabilité de 0,9 ;
- s'il fume un jour donné, il fume le jour suivant avec une probabilité de 0,6.
- Calculer $p_1$ et $q_1$. On a $p_1 = 0,9p_0 + 0,4q_0 = 0,4$ et $q_1 = 1 – p_1 = 0,6$.
- On utilise un tableur pour automatiser le calcul des termes successifs des suites $\left(p_n\right)$ et $\left(q_n\right)$. Une copie d'écran de cette feuille de calcul est fournie ci-dessous : $$ \begin {array}{|c|c|c|c|c|}\hline &A &B &C &D\\ \hline 1 &n &p_n &q_n &\\ \hline 2 &0 &0 &1 &\\ \hline 3 &1 & & &\\ \hline 4 &2 & & &\\ \hline 5 &3 & & &\\ \hline \end {array} $$ Dans la colonne A figurent les valeurs de l'entier naturel $n$. Quelles formules peut-on écrire dans les cellules B3 et C3 de façon qu'en les recopiant vers le bas, on obtienne respectivement dans les colonnes B et C les termes successifs des suites $\left(p_n\right)$ et $\left(q_n\right)$ ? En $B3$ on peut écrire : $=0,9*B2+0,4*C2$ et en $C3$ on peut écrire $=1-B3$.
- On définit les matrices $M$ et, pour tout entier naturel $n$, $X_n$ par $$M = \begin{pmatrix}0,9& 0,4\\0,1& 0,6\end{pmatrix}\quad \text{et}\quad X_n = \begin{pmatrix}p_n\\q_n \end{pmatrix}.$$ On admet que $X_{n+1} = M \times X_n$ et que, pour tout entier naturel $n$,\: $X_n = M^n \times X_0$. On définit les matrices $A$ et $B$ par $A = \begin{pmatrix}0,8&0,8\\0,2&0,2\end{pmatrix}$ et $B = \begin{pmatrix}0,2& - 0,8\\- 0,2&0,8\end{pmatrix}$.
- Démontrer que $M = A + 0,5B$. $\begin{align*} A+0,5B &= \begin{pmatrix} 0,8&0,8 \\0,2& 0,2 \end{pmatrix} + \begin{pmatrix} 0,1&-0,4\\-0,1&0,4 \end{pmatrix}\\
- Vérifier que $A^2 = A$, et que $A \times B = B \times A = \begin{pmatrix}0& 0\\0& 0\end{pmatrix}$. On admet dans la suite que, pour tout entier naturel $n$ strictement positif, $A^n = A$ et $B^n = B$. $A^2 = \begin{pmatrix} 0,8^2 + 0,8 \times 0,2&0,8^2 + 0,8 \times 0,2 \\0,8\times 0,2 + 0,2^2&0,2\times 0,8 + 0,2^2\end{pmatrix}$ $=\begin{pmatrix} 0,8 & 0,8 \\0,2&0,2\end{pmatrix}$ $=A$.
- Démontrer que, pour tout entier naturel $n$, $M^n = A + 0,5^n B$. Montrons le résultat par récurrence.
- En déduire que, pour tout entier naturel $n$ $p_n = 0,8 - 0,8 \times 0,5^n$. On a $X_n = M^n \times X_0$
- À long terme, peut-on affirmer avec certitude que le fumeur arrêtera de fumer ? $\lim\limits_{n \to +\infty} 0,5^n = 0$ donc $\lim\limits_{n \to +\infty} p_n = 0,8$.
&= \begin{pmatrix} 0,9&0,4 \\0,1&0,6 \end{pmatrix}\\
&= M
\end{align*}$
$\quad$
$A \times B = \begin{pmatrix} 0,8 \times 0,2 – 0,8 \times 0,2 & -0,8^2+0,8^2 \\0,2^2 – 0,2^2 & -0,8 \times 0,2 + 0,2 \times 0,8\end{pmatrix}$ $=\begin{pmatrix} 0&0\\0&0\end{pmatrix}$
$\quad$
$B \times A = \begin{pmatrix} 0,2 \times 0,8 – 0,8 \times 0,2 & 0,2 \times 0,8 – 0,8\times 0,2 \\-0,2 \times 0,8 + 0,2 \times 0,8 & -0,2 \times 0,8 + 0,2 \times 0,8 \end{pmatrix}$ $=\begin{pmatrix} 0&0\\0&0\end{pmatrix}$.
$\quad$
Initialisation : si $n=0$ alors $M^0 = \text{Id}$ et $A+0,5^0B = A+B = \text{Id}$
La propriété est donc vraie au rang $0$
$\quad$
Hérédité : supposons la propriété vraie au rang $n$ : $M^n=A+0,5^nB$.
$\begin{align*} M^{n+1} &= M \times M^n\\ &=(A+0,5B)\left(A + 0,5^nB\right)\\ &=A^2 +0,5^nAB + 0,5AB + 0,5^{n+1}B\\ &= A+0,5^{n+1}B \end{align*}$
La propriété est donc vraie au rang $n+1$
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire. Par conséquent, pour tout entier naturel $n$, on a $M^n = A +0,5^nB$.
$\quad$
Or $M^n = \begin{pmatrix} 0,8 + 0,5^n \times 0,2&0,8 – 0,5^n \times 0,8 \\0,2 – 0,5 ^n \times 0,2 & 0,2 + 0,5^n \times 0,8 \end{pmatrix}$
Et $X_0 = \begin{pmatrix} 0\\1\end{pmatrix}$
Donc $p_n = 0,8 – 0,5^n \times 0,8$
$\quad$
Le fumeur a donc de grande chance d’arrêter de fumer mais, puisque $\lim\limits_{n \to +\infty} p_n \neq 1$, on ne peut pas l’affirmer avec certitude.
$$\begin{cases} x=1 +t\\y=-t\\z=1+t \end{cases} \qquad t\in \mathbb R$$
$\quad$
On obtient ainsi :
$1+t – (-t)+1+t-0,5= 0 \iff 3t = -1,5 \iff t = -0,5$
On utilise cette valeur de $t$ dans les équations de $(DF)$ pour trouver les coordonnées de $M$ :
$$\begin{cases} x_M = 0,5\\y_M=0,5\\z_M=0,5 \end{cases}$$
$\quad$
$IK = \sqrt{0,5^2+0,5^2} = \sqrt{0,5}$
$KJ = \sqrt{(-1)^2+1^2} = \sqrt{2}$
Dans le triangle $IJK$ le plus grand côté est $KJ$.
Or $KJ^2 = 2$ et $IJ^2+IK^2 = 1,5+0,5=2$
Ainsi $KJ^2=IJ^2+IK^2$.
D’après la réciproque du théorème de Pythagore, le triangle $IJK$ est rectangle en $I$.
L’aire de $IJK$ est $\mathscr{A} = \dfrac{\sqrt{1,5} \times \sqrt{0,5}}{2}= \dfrac{\sqrt{0,75}}{2}$.
$MF^2=(1-0,5)^2+(-0,5)^2+(-0,5)^2 = 1,125$ ainsi $MF=\sqrt{0,75}$
Donc le volume de $FIJK$ est :
$$\mathscr{V} = \dfrac{1}{3}\times \text{Aire de la base}\times \text{Hauteur}=\dfrac{1}{3}\mathscr{B}h$$ $$\mathscr{V} = \dfrac{\sqrt{0,75}\times \sqrt{0,75}}{6} = \dfrac{0,75}{6} = \dfrac{1}{8}$$
On a $\vec{IJ}(-0,5;0,5;1)$ et $\vec{KL}(1;0,5;0)$.
Ces 2 vecteurs ne sont pas colinéaires donc les droites ne sont pas parallèles.Regardons si les droites sont sécantes. Une représentation paramétrique de $(IJ)$ est $$\begin{cases}x=0,5 -0,5t\\y=0,5t\\z=t\end{cases} \qquad t\in\mathbb R$$
Une représentation paramétrique de $(KL)$ est $$\begin{cases} x=1\\y=0,5+0,5k\\z=0,5k\end{cases} \qquad k\in\mathbb R$$
Résolvons le système : $$\begin{align*} \begin{cases}0,5-0,5t=1\\0,5t=0,5+0,5k\\t=0,5k \end{cases} &\iff \begin{cases}t=-1\\-0,5=0,5+0,5k\\-1=0,5k \end{cases}\iff \begin{cases} t=-1\\k=-2\\k=-2 \end{cases} \end{align*}$$ Les deux droites sont donc sécantes en $P(1;-0,5;-1)$.
Remarque : On pouvait aussi vérifier que le point $L$ appartient bien au plan $(IJK)$.
- On obtient ainsi deux droites coplanaires non parallèles donc sécantes.
Une figure avec Geogebra
Exercice 2 6 points
On définit la suite $\left(u_n\right)$ de la façon suivante : pour tout entier naturel $n$, $u_n = \displaystyle\int_0^1 \dfrac{x^n}{1 + x} \:\text{d}x$.
Exercice 2 6 points
On définit la suite $\left(u_n\right)$ de la façon suivante : pour tout entier naturel $n$, $u_n = \displaystyle\int_0^1 \dfrac{x^n}{1 + x} \:\text{d}x$.
Or $\lim\limits_{n \to +\infty}\dfrac{1}{n+1} = 0$, $\lim\limits_{n \to +\infty} u_{n+1} = l$ et $\lim\limits_{n \to +\infty} u_{n} = l$
Donc, en prenant les limites dans l'égalité $(1) : \;$ $\ell + \ell = 0$ soit $\ell = 0$
Exercice 3 : 3 points
On considère la courbe $\mathcal{C}$ d'équation $y = \text{e}^x$, tracée ci-dessous. 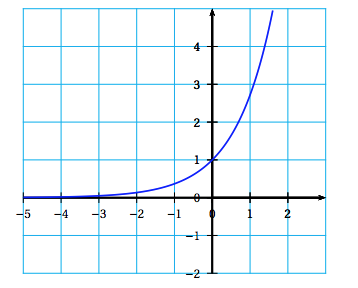
Pour tout réel $m$ strictement positif, on note $\mathcal{D}_m$ la droite d'équation $y = mx$.
Correction de l'exercice 3 (3 points)
On considère la courbe $\mathcal{C}$ d'équation $y = \text{e}^x$, tracée ci-dessous. 
Pour tout réel $m$ strictement positif, on note $\mathcal{D}_m$ la droite d'équation $y = mx$.
La tangente au point d’abscisse $1$ a pour équation $y=\text{e}^1(x-1) + \text{e}^1$ soit $y=\text{e} x$.
Ainsi $\mathscr{D}_{\text{e}}$ est bien tangente à la courbe $\mathscr{C}$ en son point d’abscisse $1$.
– si $0\le m<\text{e}$ il n’y a pas de point d’intersection
– si $m=\text{e}$ il y a un point d’intersection
– si $m>\text{e}$ il y a deux points d’intersection
$\quad$
Cette fonction est dérivable sur $\mathbb R$ en tant que somme de fonctions dérivables.
$f_m'(x)=\text{e}^x-m$.
$f_m'(x) > 0 \iff x > \ln m$.
On obtient ainsi le tableau de variations suivant :
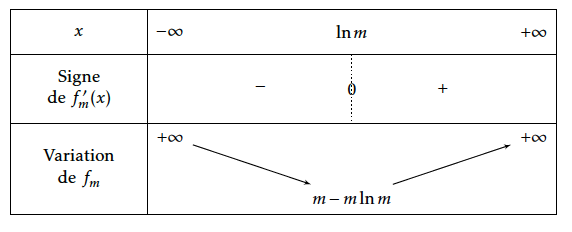
En effet $\lim\limits_{x \to +\infty} f(x) = \lim\limits_{x \to +\infty} \text{e}^x \left(1 – mx\text{e}^{-x}\right) = +\infty$.
On utilise la limite usuelle : $ \lim\limits_{x \to +\infty} \dfrac{\text{e}^x}{x}= +\infty$ , d'où on déduit $ \lim\limits_{x \to +\infty} \dfrac{x}{\text{e}^x}= 0$
Et $\lim\limits_{x\to -\infty} \text{e}^x = 0$ donc $\lim\limits_{x \to -\infty} f_m(x) = +\infty$
Si $ 0 < m < \text{e} $ alors en appliquant la fonction $\ln$ strictement croissante sur $]0;+\infty[$, $\ln m< \ln\text{e}$, soit $\ln m< 1$
Alors $1-\ln m>0$ et $m>0$, donc le minimum $m(1-\ln m )$ de $f_m$ est strictement positif.
et la fonction $f_m$ est toujours positive sur $\mathbb R$.
$\mathscr{C}$ et $\mathscr{D}_m$ n’ont donc aucun point en commun.
$\quad$
Si $m=\text{e}$ il n’y a qu’un seul point commun car $m-m\ln m =\text{e}-\text{e}\ln \text{e}= 0$
$\quad$
Si $m> \text{e}$ Ainsi $m – m\ln m = m(1-\ln m) <0$.
$\6\in \left[\5;\4\right[$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left]\2 ; \3\right]$ .
$\6\in \left[\4;\5\right[$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left[\2 ; \3\right[$ .
Il y a donc bien 2 points d’intersection.
Une animation Geogebra :
Exercice 4 5 points
En prévision d'une élection entre deux candidats A et B, un institut de sondage recueille les intentions de vote de futurs électeurs. Parmi les 1200 personnes qui ont répondu au sondage, 47 % affirment vouloir voter pour le candidat A et les autres pour le candidat B.
Compte-tenu du profil des candidats, l'institut de sondage estime que 10 % des personnes déclarant vouloir voter pour le candidat A ne disent pas la vérité et votent en réalité pour le candidat B, tandis que 20% des personnes déclarant vouloir voter pour le candidat B ne disent pas la vérité et votent en réalité pour le candidat A.
On choisit au hasard une personne ayant répondu au sondage et on note :
Correction de l'exercice 4 5 points
En prévision d'une élection entre deux candidats A et B, un institut de sondage recueille les intentions de vote de futurs électeurs. Parmi les 1200 personnes qui ont répondu au sondage, 47 % affirment vouloir voter pour le candidat A et les autres pour le candidat B.
Compte-tenu du profil des candidats, l'institut de sondage estime que 10 % des personnes déclarant vouloir voter pour le candidat A ne disent pas la vérité et votent en réalité pour le candidat B, tandis que 20% des personnes déclarant vouloir voter pour le candidat B ne disent pas la vérité et votent en réalité pour le candidat A.
On choisit au hasard une personne ayant répondu au sondage et on note :
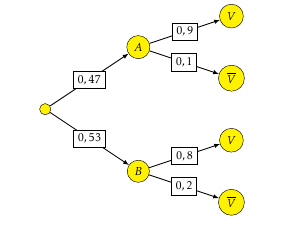
$$\begin{align*} p(A \cap V) + p\left(B \cap \overline{V}\right) &= 0,47 \times 0,9 + 0,53 \times 0,2\\ &= 0,529 \end{align*}$$
Donc $nf = 634,8 >5$ et $n(1-f) = 565,2 > 5$
On peut donc déterminer un intervalle de confiance :
$\begin{align*} I_{1~200} &= \left[0,529 – \dfrac{1}{\sqrt{1~200}};0,529 + \dfrac{1}{\sqrt{1~200}}\right]\\
& \approx [0,5001;0,5579]
\end{align*}$
Or $0,5001 > 0,5$ donc le candidat A peut croire ne sa victoire.
On a ainsi contacté $10n$ personnes et $10n \times 0,4 = 4n$ personnes ont répondu à cette enquête.
On veut donc que $4n = 1~200$ soit $n = 300$.
Il faut donc prévoir $300$ demi-heure soit $150$ heures pour que l’institut parvienne à son objectif.
Spécialité 5 points
Un fumeur décide d'arrêter de fumer. On choisit d'utiliser la modélisation suivante :
On appelle $p_n$ la probabilité de ne pas fumer le $n$-ième jour après sa décision d'arrêter de fumer et $q_n$, la probabilité de fumer le $n$-ième jour après sa décision d'arrêter de fumer. On suppose que $p_0 = 0$ et $q_0 = 1$.
Correction de l'exercice de Spécialité 5 points
Un fumeur décide d'arrêter de fumer. On choisit d'utiliser la modélisation suivante :
On appelle $p_n$ la probabilité de ne pas fumer le $n$-ième jour après sa décision d'arrêter de fumer et $q_n$, la probabilité de fumer le $n$-ième jour après sa décision d'arrêter de fumer. On suppose que $p_0 = 0$ et $q_0 = 1$.
- Vues: 34476