Baccalauréat S Nouvelle-Calédonie 17 novembre 2014
Exercice 1 5 points
Les trois parties A, B et C sont indépendantes.
Une fabrique de desserts glacés dispose d'une chaîne automatisée pour remplir des cônes de glace.
Partie A :
Les cônes de glace sont emballés individuellement puis conditionnés en lots de 2000 pour la vente en gros. On considère que la probabilité qu'un cône présente un défaut quelconque avant son conditionnement en gros est égale à $0,003$. On nomme $X$ la variable aléatoire qui, à chaque lot de 2000 cônes prélevés au hasard dans la production, associe le nombre de cônes défectueux présents dans ce lot. On suppose que la production est suffisamment importante pour que les tirages puissent être supposés indépendants les uns des autres.
- Quelle est la loi suivie par $X$ ? Justifier la réponse et préciser les paramètres de cette loi.
- Si un client reçoit un lot contenant au moins 12 cônes défectueux, l'entreprise procède alors à un échange de celui-ci. Déterminer la probabilité qu'un lot ne soit pas échangé; le résultat sera arrondi au millième.
Partie B :
Chaque cône est rempli avec de la glace à la vanille. On désigne par $Y$ la variable aléatoire qui, à chaque cône, associe la masse (exprimée en grammes) de crème glacée qu'il contient. On suppose que $Y$ suit une loi normale $\mathcal{N}\left(110 ; \sigma^2\right)$, d'espérance $\mu = 110$ et d'écart-type $\sigma$. Une glace est considérée comme commercialisable lorsque la masse de crème glacée qu'elle contient appartient à l'intervalle [104 ; 116]. Déterminer une valeur approchée à $10^{-1}$ près du paramètre $\sigma$ telle que la probabilité de l'évènement «la glace est commercialisable » soit égale à $0,98$.
Partie C :
Une étude réalisée en l'an 2000 a permis de montrer que le pourcentage de Français consommant régulièrement des glaces était de 84$\,\%$. En 2010, sur $900$ personnes interrogées, $795$ d'entre elles déclarent consommer des glaces. Peut-on affirmer, au niveau de confiance de 95$\,\%$ et à partir de l'étude de cet échantillon, que le pourcentage de Français consommant régulièrement des glaces est resté stable entre les années 2000 et 2010 ?
Correction de l'exercice 1 (5 points)
Les trois parties A, B et C sont indépendantes.
Une fabrique de desserts glacés dispose d'une chaîne automatisée pour remplir des cônes de glace.
Partie A :
Les cônes de glace sont emballés individuellement puis conditionnés en lots de 2000 pour la vente en gros. On considère que la probabilité qu'un cône présente un défaut quelconque avant son conditionnement en gros est égale à $0,003$. On nomme $X$ la variable aléatoire qui, à chaque lot de 2000 cônes prélevés au hasard dans la production, associe le nombre de cônes défectueux présents dans ce lot. On suppose que la production est suffisamment importante pour que les tirages puissent être supposés indépendants les uns des autres.
- Quelle est la loi suivie par $X$ ? Justifier la réponse et préciser les paramètres de cette loi.
- « \3 » considéré comme succès, de probabilité $p=\4$
- « \5 » considéré comme échec, de probabilité $q=1-p=\6$
- Si un client reçoit un lot contenant au moins 12 cônes défectueux, l'entreprise procède alors à un échange de celui-ci. Déterminer la probabilité qu'un lot ne soit pas échangé; le résultat sera arrondi au millième. On cherche donc $P(X \le 11) \approx 0,9801$.
On répète $\1$ fois, de façon indépendante, l’expérience «\2 » qui comporte 2 issues :
Nous sommes donc en présence d’un schéma de Bernoulli et la variable aléatoire $\7$ prenant pour valeurs le nombre de succès obtenus suit la loi binomiale de paramètres $\1$ et $\4$ notée $\mathscr{B}(\1;\4)$ .
Pour tout entier $k$ où $0\leq k\leq \1$, on a $$P(\7=k)=\binom{\1}{k}\times \left(\4\right)^k\times\left( \6\right)^{\1-k}$$
2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$
Partie B :
On a donc :
$$ \begin{array}{ll} P(104 \le Y \le 116) = 0,98 & \Leftrightarrow P(-6 \le Y – 110 \le 6) = 0,98 \\ & \Leftrightarrow P\left(-\dfrac{6}{\sigma} \le \dfrac{Y – 110}{\sigma} \le \dfrac{6}{\sigma} \right) = 0,98 \end{array}$$
La variable aléatoire $ Z =\dfrac{Y – 110}{\sigma}$ suit la loi normale centrée réduite.
On est donc ramené à trouver la valeur de $x$ telle que $P(-x \le Z \le x) = 0,98$
Or $P(-x \le Z \le x) = 2P(Z \le x) – 1$.
Par conséquent $2P(Z \le x) – 1=0,98 \Leftrightarrow P(Z \le x) = \dfrac{1,98}{2} = 0,99$
La calculatrice nous donne $x \approx 2,326$.
2ND DISTR 3Fracnormale( $\1 $ )EXE
Avec une calculatrice de type TI
$$Fracnormale( \1 ) \approx \2$$
Par conséquent $\dfrac{6}{\sigma} \approx 2,326$ et $\sigma \approx \dfrac{6}{2,326}$
Donc $\sigma \approx 2,6$
Partie C :
On note $n = 900$ et $p=0,84$.
$n = 900 \ge 30$, $np = 756 \ge 5$ et $n(1 – p) = 144 \ge 5$.
Les conditions sont donc vérifiées pour déterminer un intervalle de fluctuation asymptotique au seuil de $95\%$.
$$\begin{array} {ll}I_{900} &= \left[0,84 – 1,96\sqrt{\dfrac{0,84 \times 0,16}{900}};0,84 + 1,96\sqrt{\dfrac{0,84 \times 0,16}{900}}\right] \\ & \approx [0,816;0,864] \end{array}$$
La fréquence observée est $f = \dfrac{795}{900} \approx 0,883 \notin I_{900}$.
Le pourcentage de Français consommant régulièrement des glaces entre les années 2000 et 2010 n’est donc pas resté stable au risque d’erreur de $5\%$.
Exercice 2 5 points
Pour chaque question, une affirmation est proposée. Indiquer si chacune d'elles est vraie ou fausse, en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée. Une réponse non justifiée ne rapporte aucun point.
Une absence de réponse n'est pas pénalisée.
Dans les questions 1. et 2. , le plan est rapporté au repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. On désigne par $\mathbb R$ l'ensemble des nombres réels.
- Affirmation 1 : Le point d'affixe $(-1 + \text{i})^{10}$ est situé sur l'axe imaginaire.
- Affirmation 2 : Dans l'ensemble des nombres complexes, l'équation \[z - \overline{z} +2 - 4\text{i} = 0\] admet une solution unique.
- Affirmation 3 : $\ln \left(\sqrt{\text{e}^7} \right) + \dfrac{\ln \left(\text{e}^9 \right)}{\ln \left(\text{e}^2 \right)} = \dfrac{\text{e}^{\ln 2 + \ln 3}}{\text{e}^{\ln 3 - \ln 4}}$
- Affirmation 4 : $\displaystyle\int_0^{\ln 3} \dfrac{\text{e}^x}{\text{e}^x + 2}\:\text{d}x = - \ln \left(\dfrac{3}{5}\right)$
- Affirmation 5 : L'équation $\ln(x - 1) - \ln(x + 2) = \ln 4$ admet une solution unique dans $\mathbb R$.
Correction de l'exercice 2 (5 points)
Pour chaque question, une affirmation est proposée. Indiquer si chacune d'elles est vraie ou fausse, en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée. Une réponse non justifiée ne rapporte aucun point.
Une absence de réponse n'est pas pénalisée.
Dans les questions 1. et 2. , le plan est rapporté au repère orthonormé direct $\left(\text{O},~\vec{u},~\vec{v}\right)$. On désigne par $\mathbb R$ l'ensemble des nombres réels.
- Affirmation 1 : Le point d'affixe $(-1 + \text{i})^{10}$ est situé sur l'axe imaginaire. $|-1 + \text{i}| = \sqrt{2}$ donc $-1 + \text{i} = \sqrt{2}\left(-\dfrac{\sqrt{2}}{2} + \dfrac{\sqrt{2}}{2}\text{i}\right) = \sqrt{2}\text{e}^{-\text{i}3\pi/4}$
- Affirmation 2 : Dans l'ensemble des nombres complexes, l'équation \[z - \overline{z} +2 - 4\text{i} = 0\] admet une solution unique. On note $z = x + \text{i}z$ un nombre complexe. On a alors $z – \overline{z} = 2y\text{i}$.
- Affirmation 3 : $\ln \left(\sqrt{\text{e}^7} \right) + \dfrac{\ln \left(\text{e}^9 \right)}{\ln \left(\text{e}^2 \right)} = \dfrac{\text{e}^{\ln 2 + \ln 3}}{\text{e}^{\ln 3 - \ln 4}}$ $$\begin{array}{ll} \ln \left(\sqrt{\text{e}^7}\right) + \dfrac{\ln\left(\text{e}^9\right)}{\ln\left(\text{e}^2\right)} &= \dfrac{1}{2}\ln\left(\text{e}^7\right) + \dfrac{9}{2} \\ &= \dfrac{7}{2} + \dfrac{9}{2} \\ &=\dfrac{16}{2} \\&=8 \end{array}$$ $$\begin{array}{ll} \dfrac{\text{e}^{\ln 2 + \ln 3}}{\text{e}^{\ln 2 – \ln 4}} & = \dfrac{\text{e}^{\ln 2} \times \text{e}^{\ln 3}}{\dfrac{\text{e}^{\ln 2}}{\text{e}^{\ln 4}}} \\ &= \dfrac{2 \times 3}{\dfrac{2}{4}}\\&= 12 \\ \end{array}$$
- Affirmation 4 : $\displaystyle\int_0^{\ln 3} \dfrac{\text{e}^x}{\text{e}^x + 2}\:\text{d}x = - \ln \left(\dfrac{3}{5}\right)$ Une primitive de la fonction $f$ définie sur $\left[0;\ln 3\right]$ par $f(x) = \dfrac{\text{e}^x}{\text{e}^x + 2}$ est la fonction $F$ définie sur le même intervalle par $F(x) = \ln \left(\text{e}^x + 2\right)$
- Affirmation 5 : L'équation $\ln(x - 1) - \ln(x + 2) = \ln 4$ admet une solution unique dans $\mathbb R$. Les solutions de l’équation doivent vérifier $x – 1> 0$ et $x + 2> 0$ soit $x > 1$.
Un argument de $(-1 + \text{i})^{10}$ est donc $- \dfrac{3\pi}{4} \times 10 = -\dfrac{15\pi}{2}$.
Le nombre $(-1 + \text{i})^{10}$ est donc un imaginaire pur.
Affirmation vraie
L’équation $z-\overline{z} + 2 – 4\text{i} = 0$ est donc équivalente à $2y\text{i} + 2 -4\text{i} = 0$ qui ne possède aucune solution.
Affirmation fausse
Affirmation fausse
On a ainsi :
$$\begin{array}{ll} I = \displaystyle \int_0^{\ln 3} \dfrac{\text{e}^x}{\text{e}^x + 2}\text{d}x & = F(\ln 3) – F(0) \\ &= \ln\left(\text{e}^{\ln3} + 2\right) – \ln 2 \\
&=\ln 5 – \ln 2 \\ &= \ln \left(\dfrac{5}{2}\right) \\ &= -\ln\left(\dfrac{2}{5}\right) \end{array}$$
Affirmation vraie
$$\begin{array}{ll} \ln(x – 1) – \ln(x + 2) = \ln 4 & \Leftrightarrow \ln \dfrac{x – 1}{x + 2} = \ln 4 \quad \text{et } x > 1\\ & \Leftrightarrow \dfrac{x-1}{x+2} = 4 \quad \text{et } x > 1 \\ & \Leftrightarrow x – 1 = 4(x + 2) \quad \text{et } x > 1 \\ & \Leftrightarrow 3x = -9 \quad \text{et } x > 1 \\ & \Leftrightarrow x = -3 \quad \text{et } x > 1 \end{array}$$
L’équation ne possède donc pas de solution dans $\mathbb R$
Affirmation fausse
-
- Déterminer les coordonnées des points I, J et K.
- Démontrer que les points I, J et K définissent un plan.
- Montrer que le vecteur $\vec{n}$ de coordonnées $(3~;~1~;~4)$ est un vecteur normal au plan (IJK). En déduire une équation cartésienne de ce plan.
- Soit $\mathcal{P}$ le plan d'équation $3x + y + 4z - 8 = 0$.
- Déterminer une représentation paramétrique de la droite (BD).
- Démontrer que le plan $\mathcal{P}$ et la droite (BD) sont sécants et donner les coordonnées de L, point d'intersection du plan $\mathcal{P}$ et de la droite (BD).
- Le point L est-il le symétrique du point D par rapport au point B ?
-
- Déterminer les coordonnées des points I, J et K. $I$ est le milieu de $[AB]$ donc $I(1;1;1)$.
- Démontrer que les points I, J et K définissent un plan. $\vec{IJ}(2;2;-2)$ et $\vec{IK}(-2;2;1)$. $\dfrac{2}{-2} \ne \dfrac{2}{2}$
- Montrer que le vecteur $\vec{n}$ de coordonnées $(3~;~1~;~4)$ est un vecteur normal au plan (IJK). En déduire une équation cartésienne de ce plan. $\vec{n}.\vec{IJ} = 3 \times 2 + 1 \times 2 + 4 \times (-2) = 0$
$J$ est le milieu de $[CD]$ donc $J(3;3;-1)$
$$\begin{array}{ll} \vec{BK} = \dfrac{1}{3}\vec{BC} & \Leftrightarrow \begin{cases} x_k – 1 = \dfrac{1}{3}(-5 – 1) \\ y_k – 2 = \dfrac{1}{3}(5 – 2) \\z_k – 3 = \dfrac{1}{3}(0 – 3) \end{cases} \\
& \Leftrightarrow \begin{cases} x_k – 1 = -2 \\y_k – 2= 1 \\z_k – 3 = -1 \end{cases} & \Leftrightarrow \begin{cases} x_k = -1 \\y_k = 3 \\z_k = 2 \end{cases}
\end{array}$$
Donc $K(-1;3;2)$.
Ces deux vecteurs n’étant pas colinéaires,car leurs coordonnées ne sont pas proportionnelles. les points $I$, $J$ et $K$ définissent bien un plan.
$\vec{n}.\vec{Ik} = 3 \times (-2) + 1 \times 2 + 4 \times 1 = 0$
Le vecteur $\vec{n}$ est orthogonal à deux vecteurs non colinéaires du plan $(IJK)$. Il est donc normal au plan $(IJK)$.
$\quad$
Une équation du plan $(IJK)$ est donc de la forme $3x + y + 4z + d = 0$.
Puisque $I$ appartient à ce plan, on a $3 + 1 + 4 + d = 0$ soit $d= -8$.
Une équation du plan $(IJK)$ est donc :$$3x+y+4z-8=0$$ - Soit $\mathcal{P}$ le plan d'équation $3x + y + 4z - 8 = 0$.
- Déterminer une représentation paramétrique de la droite (BD). Un vecteur directeur de $(BD)$ est $\vec{BD}(10;-1;-5)$. La droite $(BD)$ passe par le point $B$, donc une représentation paramétrique de cette droite est : $$\begin{cases}x = 1 + 10t\\y = 2 – t \qquad t\in \mathbb R \\z=3 – 5t \end{cases}$$
- Démontrer que le plan $\mathcal{P}$ et la droite (BD) sont sécants et donner les coordonnées de L, point d'intersection du plan $\mathcal{P}$ et de la droite (BD). $\vec{n}$ est un vecteur normal au plan $\mathscr{P}$.
- Le point L est-il le symétrique du point D par rapport au point B ? Déterminons les coordonnées du milieu $E$ de $[LD]$ : $E(1;2;3) = B$.
$\vec{BD}.\vec{n} = 10 \times 3 – 1 \times 1 – 5 \times 4 = 9\ne 0$
Par conséquent la droite $(BD)$ n’est pas parallèle au plan $\mathscr{P}$. Ils sont donc sécants.
$\quad$
Leur point d’intersection vérifie donc leurs équations. On obtient ainsi :
$3(1 + 10t) + (2 – t) + 4(3 -5t) – 8 = 0 \Leftrightarrow 9t+9=0$ $\Leftrightarrow t = -1$.
Par conséquent $\begin{cases} x_L = 1 – 10 = -9\\y_L = 2 + 1 = 3\\z_L = 3 + 5 = 8 \end{cases}$
Le point $L$ est donc le symétrique du point $D$ par rapport au point $B$. Une figure faite avec GeoGebra3D - Démontrer que $f$ est croissante sur l'intervalle $[0~;~+ \infty[$.
- Résoudre l'équation $f(x) = x$ sur l'intervalle $[0~;~+ \infty[$. On note $\alpha$ la solution. On donnera la valeur exacte de $\alpha$ puis on en donnera une valeur approchée à $10^{-2}$ près.
- On considère la suite $\left(u_n\right)$ définie par $u_0 = 1$ et, pour tout entier naturel $n$ $u_{n+1} = f\left(u_n\right)$.
Sur la figure de annexe 1 , en utilisant la courbe $\mathcal{C}$ et la droite $\mathcal{D}$, placer les points $M_0, M_1$ et $M_2$ d'ordonnée nulle et d'abscisses respectives $u_0,\: u_1$ et $u_2$.
Quelles conjectures peut-on faire sur le sens de variation et la convergence de la suite $\left(u_n\right)$ ? -
- Démontrer, par récurrence, que, pour tout entier naturel $n$, \[0 \leqslant u_n \leqslant u_{n+1} \leqslant \alpha\] où $\alpha$ est le réel défini dans la question 2.
- Peut-on affirmer que la suite $\left(u_n\right)$ est convergente ? On justifiera la réponse.
- Pour tout entier naturel $n$, on définit la suite $\left(S_n\right)$ par \[S_n = \displaystyle\sum_{k=0}^{n} u_k = u_0 + u_1 + \cdots + u_n.\]
- Calculer $S_0, \:S_1$ et $S_2$. Donner une valeur approchée des résultats à $10^{-2}$ près.
- Compléter l'algorithme donné en \textbf{annexe 2} pour qu'il affiche la somme $S_n$ pour la valeur de l'entier $n$ demandée à l'utilisateur.
- Montrer que la suite $\left(S_n\right)$ diverge vers $+ \infty$.
- Démontrer que $f$ est croissante sur l'intervalle $[0~;~+ \infty[$. La fonction $x \mapsto \dfrac{1}{x+2}$ est une fonction décroissante sur $[0;+\infty[$. Par conséquent la fonction $x \mapsto \dfrac{-4}{x+2}$ et la fonction $f$ sont croissantes sur cet intervalle.
- Résoudre l'équation $f(x) = x$ sur l'intervalle $[0~;~+ \infty[$. On note $\alpha$ la solution. On donnera la valeur exacte de $\alpha$ puis on en donnera une valeur approchée à $10^{-2}$ près. $$\begin{array}{ll} f(x) = x & \Leftrightarrow 5 – \dfrac{4}{x+2} = x \\ & \Leftrightarrow 5(x +2) -4 = x(x+2) \\ & \Leftrightarrow 5x + 10 – 4 = x^2 + 2x \\ & \Leftrightarrow x^2 – 3x – 6 = 0 \end{array}$$
- On considère la suite $\left(u_n\right)$ définie par $u_0 = 1$ et, pour tout entier naturel $n$ $u_{n+1} = f\left(u_n\right)$.
Sur la figure de annexe 1 , en utilisant la courbe $\mathcal{C}$ et la droite $\mathcal{D}$, placer les points $M_0, M_1$ et $M_2$ d'ordonnée nulle et d'abscisses respectives $u_0,\: u_1$ et $u_2$.
Quelles conjectures peut-on faire sur le sens de variation et la convergence de la suite $\left(u_n\right)$ ? -
- Démontrer, par récurrence, que, pour tout entier naturel $n$, \[0 \leqslant u_n \leqslant u_{n+1} \leqslant \alpha\] où $\alpha$ est le réel défini dans la question 2. Initialisation : si $n=0$ alors $u_0 = 1$ et $u_1 = f(u_0) = \dfrac{11}{3}$ et $0 \le 1 \le \dfrac{11}{3} \le \alpha$
- Peut-on affirmer que la suite $\left(u_n\right)$ est convergente ? On justifiera la réponse. La suite $(u_n)$ est croissante et majorée par $\alpha$. On peut donc affirmer qu’elle converge.
La propriété est vraie au rang $0$.
$\quad$
Hérédité : Supposons la vraie au rang $n$ : $0 \le u_n \le u_{n+1} \le \alpha$
Puisque la fonction $f$ est croissante on a $f(0) \le f(u_n) \le f(u_{n+1}) \le f(\alpha)$ soit $3 \le u_{n+1} \le u_{n+2} \le \alpha$.
On a donc bien $0 \le u_{n+1} \le u_{n+2} \le \alpha$.
La propriété est vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$. En la supposant vraie au rang $n$, elle est encore vraie au rang suivant.
Par conséquent, pour tout entier naturel $n$ on a : $0 \le u_n \le u_{n+1} \le \alpha$
- Pour tout entier naturel $n$, on définit la suite $\left(S_n\right)$ par \[S_n = \displaystyle\sum_{k=0}^{n} u_k = u_0 + u_1 + \cdots + u_n.\]
- Calculer $S_0, \:S_1$ et $S_2$. Donner une valeur approchée des résultats à $10^{-2}$ près. $S_0 = u_0 = 1$
- Compléter l'algorithme donné en \textbf{annexe 2} pour qu'il affiche la somme $S_n$ pour la valeur de l'entier $n$ demandée à l'utilisateur. Entrée :
- Montrer que la suite $\left(S_n\right)$ diverge vers $+ \infty$. La suite $(u_n)$ étant croissante on a $u_n \ge u_0$ pour tout $n \in \mathbb N$
$S_1 = u_0 + u_1 = 1 +\dfrac{11}{3} = \dfrac{14}{3} \approx 4,67$
$S_2 = S_1 + u_2 = \dfrac{14}{3} + \dfrac{73}{17} = \dfrac{457}{51} \approx 8,96$
$\quad$
$\quad$ $n$ un entier naturel
Variables :
$\quad$ $u $et $s$ sont des variables réelles
$\quad$ $n$ et $i$ sont des variables entières
Initialisation :
$\quad$ $u$ prend la valeur $1$
$\quad$ $s$ prend la valeur $u$
$\quad$ $i$ prend la valeur $0$
$\quad$ Demander la valeur de $n$
Traitement :
$\quad$ Tant que $i < n$
$\qquad$ Affecter à $i$ la valeur $i+1$
$\qquad$ Affecter à $u$ la valeur $5 – \dfrac{4}{u+2}$
$\qquad$ Affecter à $s$ la valeur $s + u$
$\quad$ Fin Tant que
Sortie :
$\quad$ Afficher $s$
$\quad$
Par conséquent $S_n \ge (n+1)u_0$ soit $S_n \ge n+1$.
Mais $\lim\limits_{n \to +\infty }n+1 = +\infty$.
D’après le théorème de comparaison on a $\lim\limits_{n \to +\infty} S_n = +\infty$. - On entre $A = 12$ et $B = 14$. En remplissant le tableau donné en annexe , déterminer la valeur affichée par l'algorithme.
- Cet algorithme calcule la valeur du PGCD des nombres $A$ et $B$. En entrant $A = 221$ et $B = 331$, l'algorithme affiche la valeur 1.
- Justifier qu'il existe des couples $(x~;~y)$ d'entiers relatifs solutions de l'équation \[(\text{E})\qquad 221x - 331y = 1.\]
- Vérifier que le couple $(3~;~2)$ est une solution de l'équation (E). En déduire l'ensemble des couples $(x~;~y)$ d'entiers relatifs solutions de l'équation (E).
- On considère les suites d'entiers naturels $\left(u_n\right)$ et $\left(v_n\right)$ définies pour tout entier naturel $n$ par \[u_n = 2 + 221n \quad \text{et} \quad \left\{\begin{array}{l c l} v_0& =& 3\\ v_{n+1}&=& v_n + 331 \end{array}\right.\]
- Exprimer $v_n$ en fonction de l'entier naturel $n$.
- Déterminer tous les couples d'entiers naturels $(p~;~q)$ tels que $u_p = v_q,\quad 0 \leqslant p \leqslant 500\quad$ et $\quad0 \leqslant q \leqslant 500$.
- On entre $A = 12$ et $B = 14$. En remplissant le tableau donné en annexe , déterminer la valeur affichée par l'algorithme. $$\begin{array}{|c|c|c|} \hline A&B&D \\ \hline 12&14&2\\ \hline 2&12&10\\ \hline 10&2&8\\ \hline 8&10&2\\ \hline 2&8&6\\ \hline 6&2&4\\ \hline 4&6&2\\ \hline 2&4&2\\ \hline 2&2&0\\ \hline \end{array}$$ L’algorithme affiche donc $2$.
- Cet algorithme calcule la valeur du PGCD des nombres $A$ et $B$. En entrant $A = 221$ et $B = 331$, l'algorithme affiche la valeur 1.
- Justifier qu'il existe des couples $(x~;~y)$ d'entiers relatifs solutions de l'équation \[(\text{E})\qquad 221x - 331y = 1.\] Les nombres $221$ et $331$ sont premiers entre eux. D’après le théorème de Bezout, il existe un couple d’entier relatif $(a;b)$ tel que $221a+331b=1$ soit $221a – 331\times (-b) = 1$
- Vérifier que le couple $(3~;~2)$ est une solution de l'équation (E). En déduire l'ensemble des couples $(x~;~y)$ d'entiers relatifs solutions de l'équation (E). $221 \times 3 – 331 \times 2 = 663 – 662 = 1$.
Le couple $(a;-b)$ est donc solution de l’équation $(E)$.
Le couple $(3;2)$ est donc une solution de l’équation $(E)$.
Soit $(x;y)$ un autre couple solution.
On a ainsi :
$221x – 331y = 1$ et $221 \times 3 – 331 \times 2 = 1$.
Par différence on obtient :
$221(x – 3) – 331(y – 2) = 0$ soit $221(x – 3) = 331(y – 2)$
$221$ et $331$ sont premiers entre eux. D’après le théorème de Gauss, il existe un entier relatif $k \in \mathbb Z$ tel que :
$x-3 = 331k$ et $y-2 = 221k$.
D’où $x= 3 + 331k$ et $y = 2 +221k$.
Réciproquement :
Soit $k$ un entier relatif.
$221(3 +331k) – 331(2 + 221k) = 663 + 221 \times 331k – 662 – 331 \times 221k = 1$.
Les solutions de l’équation $(E)$ sont les couples $(3+331k;2+221k)$ pour tout $k \in \mathbb Z$. - On considère les suites d'entiers naturels $\left(u_n\right)$ et $\left(v_n\right)$ définies pour tout entier naturel $n$ par \[u_n = 2 + 221n \quad \text{et} \quad \left\{\begin{array}{l c l} v_0& =& 3\\ v_{n+1}&=& v_n + 331 \end{array}\right.\]
- Exprimer $v_n$ en fonction de l'entier naturel $n$. $(v_n)$ est une suite arithmétique de raison $331$ et de premier terme $3$.
- Déterminer tous les couples d'entiers naturels $(p~;~q)$ tels que $u_p = v_q,\quad 0 \leqslant p \leqslant 500\quad$ et $\quad0 \leqslant q \leqslant 500$. On cherche les couples d’entiers naturels $(p;q)$ tels que $2 +221p = 3 +331q$ soit $221p – 331q = 1$.
Donc $v_n = 3 + 331n$ pour tout entier naturel $n$.
Il s’agit des couples solutions de l’équation $(E)$.
On veut donc que : $0 \le 3 +331k \le 500$ et $0 \le 2+221k \le 500$
d’où $-3 \le 331k \le 497$ et $-2 \le 221k \le 498$
soit finalement $\dfrac{-k}{331} \le k \le \dfrac{497}{331}$ et $\dfrac{-2}{221} \le k \le \dfrac{498}{221}$.
Par conséquent $k\in \{0;1\}$.
Les couples $(p;q)$ cherchés sont donc $(3;2)$ et $(334;223)$.
Exercice 3 5 points
L'espace est rapporté à un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$ . On donne les points A$(1~;~0~;~- 1)$, B$(1~;~2~;~3)$, C$(-5~;~5~;~0)$ et D$(11~;~1~;~-2)$. Les points I et J sont les milieux respectifs des segments [AB] et [CD]. Le point K est défini par $\vec{\text{BK}} = \dfrac{1}{3}\vec{\text{BC}}$.
Correction de l'exercice 3 (5 points)
L'espace est rapporté à un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$ . On donne les points A$(1~;~0~;~- 1)$, B$(1~;~2~;~3)$, C$(-5~;~5~;~0)$ et D$(11~;~1~;~-2)$. Les points I et J sont les milieux respectifs des segments [AB] et [CD]. Le point K est défini par $\vec{\text{BK}} = \dfrac{1}{3}\vec{\text{BC}}$.

Exercice 4 5 points
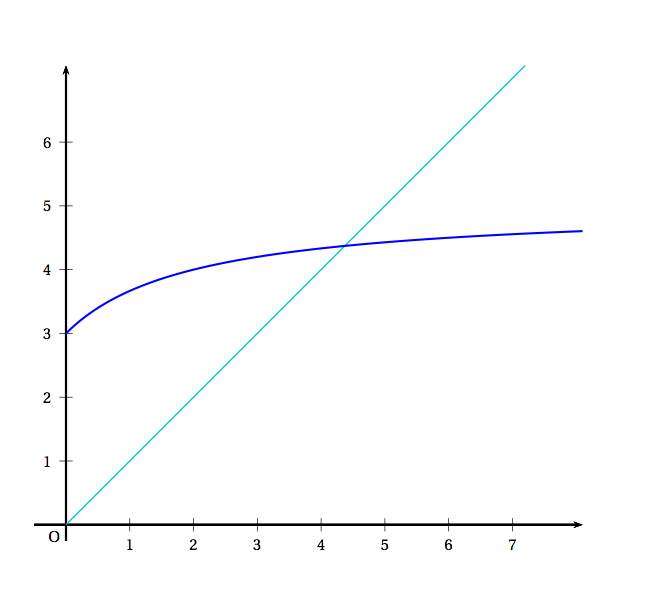
On considère la fonction $f$ définie sur l'intervalle $[0~;~+ \infty[$ par \[f(x) = 5 - \dfrac{4}{x + 2}.\] On admettra que $f$ est dérivable sur l'intervalle $[0~;~+ \infty[$. On a tracé en annexe 1 dans un repère orthonormé la courbe $\mathcal{C}$ représentative de $f$
ainsi que la droite $\mathcal{D}$ d'équation $y = x$.
Annexe 1:
Annexe 2 de l'exercice 4 à rendre avec la copie réservé aux candidats n'ayant pas suivi l'enseignementde spécialité
$$\begin{array}{|l l|}\hline \text{Entrée :}& n \text{ un entier naturel} \\ \text{Variables :} & u \text{ et } s \text{ sont des variables réelles}\\ & n \text{ et } i \text{ sont des variables entières}\\ \text{Initialisation :} & u \text{ prend la valeur } 1 \\ & s \text{ prend la valeur} u \\ & i \text{ prend la valeur } 0\\ &\text{ Demander la valeur de } n \\ \text{Traitement :}&\text{ Tant que }\ldots\\ &\text{ Affecter à }i \text{ la valeur }i + 1\\ &\text{ Affecter à } u \text{ la valeur } \ldots\\ & \text{ Affecter à }s \text{ la valeur } \ldots\\ &\text{ Fin Tant que } \\ \text{Sortie :} &\text{ Afficher } s.\\ \hline \end{array}$$
Correction de l'exercice 4 5 points
On considère la fonction $f$ définie sur l'intervalle $[0~;~+ \infty[$ par \[f(x) = 5 - \dfrac{4}{x + 2}.\] On admettra que $f$ est dérivable sur l'intervalle $[0~;~+ \infty[$. On a tracé en annexe 1 dans un repère orthonormé la courbe $\mathcal{C}$ représentative de $f$
ainsi que la droite $\mathcal{D}$ d'équation $y = x$.
NB : on pouvait évidemment utiliser la dérivée également mais cela change un peu.
On calcule le discriminant : $\Delta = 9 + 24 = 33 > 0$
Cette équation possède deux solutions réelles $x_1 = \dfrac{3 – \sqrt{33}}{2} <0$ et $x_2 = \dfrac{3 + \sqrt{33}}{2} > 0$.
Par conséquent $\alpha = \dfrac{3 + \sqrt{33}}{2} \approx 4,37$
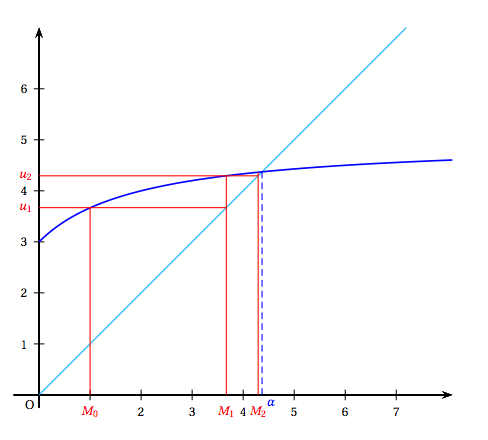
Il semblerait que la suite $(u_n)$ soit croissante et converge vers environ $4,3$
Spécialité 5 points
On considère l'algorithme suivant, où $A$ et $B$ sont des entiers naturels tels que $A < B$ : $$\begin{array}{|l l|}\hline \text{ Entrées :}& A \text{ et }B \text{ entiers naturels tels que } A < B\\ &\\ \text{ Variables :}& D \text{ est un entier}\\ &\text{ Les variables d'entrées } A \text{ et } B \\ &\\ \text{ Traitement :}&\\ &\text{ Affecter à } D \text{ la valeur de } B - A\\ &\\ &\text{ Tant que } D > 0\\ &B \text{ prend la valeur de } A\\ &A \text{ prend la valeur de } D\\ & \text{ Si }B > A \text{ Alors }\\ & D \text{ prend la valeur de } B - A\\ & \text{ Sinon }\\ & D \text{ prend la valeur de } A - B\\ &\text{ Fin Si }\\ &\text{ Fin Tant que }\\ &\\ \text{ Sortie :} &\text{ Afficher } A\\ \hline \end{array} $$
Correction de l'exercice de Spécialité 5 points
On considère l'algorithme suivant, où $A$ et $B$ sont des entiers naturels tels que $A < B$ : $$\begin{array}{|l l|}\hline \text{ Entrées :}& A \text{ et }B \text{ entiers naturels tels que } A < B\\ &\\ \text{ Variables :}& D \text{ est un entier}\\ &\text{ Les variables d'entrées } A \text{ et } B \\ &\\ \text{ Traitement :}&\\ &\text{ Affecter à } D \text{ la valeur de } B - A\\ &\\ &\text{ Tant que } D > 0\\ &B \text{ prend la valeur de } A\\ &A \text{ prend la valeur de } D\\ & \text{ Si }B > A \text{ Alors }\\ & D \text{ prend la valeur de } B - A\\ & \text{ Sinon }\\ & D \text{ prend la valeur de } A - B\\ &\text{ Fin Si }\\ &\text{ Fin Tant que }\\ &\\ \text{ Sortie :} &\text{ Afficher } A\\ \hline \end{array} $$
- Vues: 38572