Baccalauréat S Antilles-Guyane 18 juin 2013
Page 1 sur 11
Exercice 1 5 points
Description de la figure dans l'espace muni du repère orthonormé $\left(A ; \vec{AB} ; \vec{AD} ; \vec{AE}\right)$: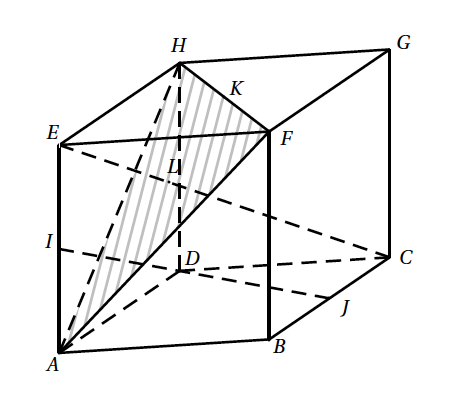
- $ABCDEFGH$ désigne un cube de côté 1.
- On appelle $\mathcal{P}$ le plan $(AFH)$.
- Le point $I$ est le milieu du segment $[AE]$,
- le point $J$ est le milieu du segment $[BC]$,
- le point $K$ est le milieu du segment $[HF]$,
- le point $L$ est le point d'intersection de la droite $(EC)$ et du plan $\mathcal{P}$.
Ceci est un questionnaire à choix multiples (QCM). Pour chacune des questions, une seule des quatre affirmations est exacte. Le candidat indiquera sur sa copie le numéro de la question et la lettre correspondant à la réponse choisie. Aucune justification n'est demandée.
Une réponse exacte rapporte un point, une réponse fausse ou une absence de réponse ne rapporte aucun point.
-
- Les droites $(IJ)$ et $(EC)$ sont strictement parallèles.
- Les droites $(IJ)$ et $(EC)$ sont non coplanaires.
- Les droites $(IJ)$ et $(EC)$ sont sécantes.
- Les droites $(IJ)$ et $(EC)$ sont confondues.
-
- Le produit scalaire $\vec{AF}\cdot\vec{BG}$ est égal à 0.
- Le produit scalaire $\vec{AF}\cdot\vec{BG}$ est égal à $(-1)$.
- Le produit scalaire $\vec{AF}\cdot\vec{BG}$ est égal à 1.
- Le produit scalaire $\vec{AF}\cdot\vec{BG}$ est égal à 2.
- Dans le repère orthonormé $\left(A ; \vec{AB} ; \vec{AD} ; \vec{AE}\right)$:
- Le plan $\mathcal{P}$ a pour équation cartésienne : $x + y + z - 1=0$.
- Le plan $\mathcal{P}$ a pour équation cartésienne : $x- y + z=0$.
- Le plan $\mathcal{P}$ a pour équation cartésienne : $- x + y + z=0$.
- Le plan $\mathcal{P}$ a pour équation cartésienne : $x + y - z = 0$.
-
- $\vec{EG}$ est un vecteur normal au plan $\mathcal{P}$.
- $\vec{EL}$ est un vecteur normal au plan $\mathcal{P}$.
- $\vec{IJ}$ est un vecteur normal au plan $\mathcal{P}$.
- $\vec{DI}$ est un vecteur normal au plan $\mathcal{P}$.
-
- $\vec{AL}=\frac12\vec{AH} + \frac12\vec{AF}$.
- $\vec{AL}=\frac13\vec{AK}$.
- $\vec{ID}=\frac12\vec{IJ}$.
- $\vec{AL}=\frac13\vec{AB}+\frac13\vec{AD}+\frac23\vec{AE}$.
- Vues: 48953
