Baccalauréat STI 2D/STL spécialité SPCL Métropole- La Réunion 8 septembre 2016

Exercice 1 6 points

Fonction exponentielle

Dans cet exercice, la température est exprimée en degrés Celsius (°C) et le temps $t$ est exprimé en minutes. Dans une entreprise de fabrication de pièces métalliques, un ouvrier doit manipuler des plaques chaudes pendant une dizaine de secondes. À la sortie du four, les plaques sont à une température de 30 °C et disposées dans une pièce dont la température ambiante est maintenue à 26 °C par un système de ventilation. La commission de sécurité prescrit qu'avec les gants actuels, l'ouvrier doit attendre 10 minutes pour manipuler les plaques à leur sortie du four. Afin de réduire ce délai d'attente, le directeur s'interroge sur l'achat de nouveaux gants dont les caractéristiques techniques établies par la commission de sécurité sont les suivantes :

• Sans couture.
• Très doux et confortables.
• Température maximale d'utilisation : 240 °C.

1. Dans cette question, on ne demande pas de justification.
   1. Quelle est, à la sortie du four, la température des plaques ?
   2. Comment varie, à la sortie du four, la température des plaques au cours du temps ?
   3. Vers quelle valeur la température des plaques devrait-elle se stabiliser ?
2. La température d'une plaque depuis sa sortie du four, est modélisée en fonction du temps $t$, exprimé en minutes, par une fonction $g$. On admet que cette fonction $g$ est définie sur l'intervalle $[0~;~+\infty [$ par $g(t) = 274 e^{at} + 26$ où $a$ est un nombre réel.
   1. Calculer $g(0)$. Ce résultat est-il conforme aux données ?
   2. D'après la question 1, quel doit être le signe du nombre réel $a$ ?
   3. On sait que 3 minutes après sa sortie du four la température de la plaque, arrondie à l'unité, est de 262 °C. Montrer que la valeur approchée à $10^{-2}$ près du coefficient $a$ est $-0,05$.
3. Dans cette question on considère que, pour tout nombre réel $t$ de l'intervalle $[0 ; +\infty [$ : \[ g(t)=274 e^{-0,05t}+26 .\]
   1. Avec les gants actuellement utilisés, à quelle température l'ouvrier pourra-t-il manipuler les plaques après leur sortie du four, en respectant les caractéristiques techniques de la commission de sécurité ?
   2. Si le directeur décidait d'équiper les ouvriers avec les nouveaux gants, quel délai d'attente minimal serait requis avant que les ouvriers puissent manipuler les plaques ?
   3. En déduire le gain de temps, en pourcentage, dû à l'utilisation de ces nouveaux gants.

Correction de l'exercice 1 (6 points)

Fonction exponentielle

Dans cet exercice, la température est exprimée en degrés Celsius (°C) et le temps $t$ est exprimé en minutes. Dans une entreprise de fabrication de pièces métalliques, un ouvrier doit manipuler des plaques chaudes pendant une dizaine de secondes. À la sortie du four, les plaques sont à une température de 30 °C et disposées dans une pièce dont la température ambiante est maintenue à 26 °C par un système de ventilation. La commission de sécurité prescrit qu'avec les gants actuels, l'ouvrier doit attendre 10 minutes pour manipuler les plaques à leur sortie du four. Afin de réduire ce délai d'attente, le directeur s'interroge sur l'achat de nouveaux gants dont les caractéristiques techniques établies par la commission de sécurité sont les suivantes :

• Sans couture.
• Très doux et confortables.
• Température maximale d'utilisation : 240 °C.

1. Dans cette question, on ne demande pas de justification.
   1. Quelle est, à la sortie du four, la température des plaques ?
   À la sortie du four, les plaques sont à une température de 300°C.
   2. Comment varie, à la sortie du four, la température des plaques au cours du temps ?
   À la sortie du four, les plaques sont disposées dans une pièce dont la température ambiante est maintenue à 26°C donc la température des plaques va baisser.
   3. Vers quelle valeur la température des plaques devrait-elle se stabiliser ?
   La température de la pièce est maintenue à 26°C donc la température des plaques devrait-elle se stabiliser à 26°C.
2. La température d'une plaque depuis sa sortie du four, est modélisée en fonction du temps $t$, exprimé en minutes, par une fonction $g$. On admet que cette fonction $g$ est définie sur l'intervalle $[0~;~+\infty [$ par $g(t) = 274 e^{at} + 26$ où $a$ est un nombre réel.
   1. Calculer $g(0)$. Ce résultat est-il conforme aux données ?
   $$g⁡(0)=274\times e^{0}+26=300$$
   2. D'après la question 1, quel doit être le signe du nombre réel $a$ ?
   Comme la fonction $g$ est décroissante, le nombre réel $a$ est négatif.
   3. On sait que 3 minutes après sa sortie du four la température de la plaque, arrondie à l'unité, est de 262 °C. Montrer que la valeur approchée à $10^{-2}$ près du coefficient $a$ est $-0,05$.
   Le nombre réel $a$ est solution de l'équation : $$\begin{array}{rl} g(3)=262 & \iff 274 e^{3a} + 26= 262 \\ & \iff 274 e^{3a} = 236 \\ &\iff e^{3a} = \dfrac{236}{274} \\ &\iff 3a =\ln\left (\dfrac{236}{274}\right )\\ &\iff a= \dfrac{\ln\left (\dfrac{236}{274}\right )}{3}\approx - 0, 05 \end{array}$$ La valeur approchée à $10^{-2}$ près du coefficient $a$ est $a\approx -0,05$.
3. Dans cette question on considère que, pour tout nombre réel $t$ de l'intervalle $[0 ; +\infty [$ : \[ g(t)=274 e^{-0,05t}+26 .\]
   1. Avec les gants actuellement utilisés, à quelle température l'ouvrier pourra-t-il manipuler les plaques après leur sortie du four, en respectant les caractéristiques techniques de la commission de sécurité ?
   $g(10 ) = 274 e^{-0,5} + 26\approx 192$ Avec les gants actuellement utilisés, l'ouvrier pourra manipuler les plaques à la température de 192°C.
   2. Si le directeur décidait d'équiper les ouvriers avec les nouveaux gants, quel délai d'attente minimal serait requis avant que les ouvriers puissent manipuler les plaques ?
   Le délai d'attente $t$ est solution de l'inéquation : $$\begin{array}{rl} g(t)\leq 240& \iff 274 e^{-0,05t} + 26\leq 240\\ & \iff 274 e^{-0,05t} \leq 214\\ & \iff e^{-0,05t} \leq \dfrac{214}{274}\\ & \iff \ln\left ( e^{-0,05t}\right ) \leq \ln\left (\dfrac{214}{274}\right )\\ & \iff -0,05t \leq \ln\left (\dfrac{214}{274}\right )\\ & \iff t \geq \dfrac{ \ln\left (\dfrac{214}{274}\right )}{-0,05}\\ & \iff t \geq 20 \ln\left (\dfrac{137}{107}\right ) \\ \end{array}$$ Comme $20 \ln\left (\dfrac{137}{107}\right ) \approx 4,943$, on en déduit que : Avec les nouveaux gants, l'ouvrier pourra manipuler les plaques au bout de 5 minutes.
   3. En déduire le gain de temps, en pourcentage, dû à l'utilisation de ces nouveaux gants.
   
   Avec les nouveaux gants, le temps d'attente est divisé par deux soit un gain de 50%.

Exercice 2 4 points

Probabilités

Les parties A et B sont indépendantes. Dans cet exercice, toutes les probabilités demandées seront arrondies à $10^{-3}$.
Une usine métallurgique fabrique des boîtes de conserve pour des entreprises spécialisées dans le conditionnement industriel de légumes. La probabilité qu'une boîte prélevée au hasard soit non conforme est 0,04. Un lot de 200 boîtes choisies au hasard est livré à une entreprise spécialisée dans le conditionnement des légumes. Le nombre de boîtes fabriquées par cette usine métallurgique est assez important pour pouvoir assimiler un tel prélèvement à un tirage avec remise de 200 boîtes.

Partie A

La variable aléatoire $X$ désigne le nombre de boîtes non conformes dans un tel lot.

1. Justifier que la variable aléatoire $X$ suit une loi binomiale dont on précisera les paramètres.
2. Déterminer la probabilité qu'un tel lot contienne exactement quatre boîtes non conformes.

Partie B

On décide d'approcher la loi binomiale suivie par $X$ par la loi normale d'espérance $\mu = 8$ et d'écart type $\sigma = 2,77$.

1. Justifier le choix de ces paramètres.
2. À l'aide de la loi normale ainsi définie :
   1. calculer $P(6 \leqslant X \leqslant 10)$ et interpréter le résultat trouvé ;
   2. déterminer une approximation de la probabilité qu'il y ait au maximum 4 boîtes non conformes.

Partie C

Dans le lot livré de 200 boîtes, on compte 11 boîtes non conformes. Le fabricant des boîtes est averti. Doit-il s'inquiéter ?
On pourra utiliser un intervalle de fluctuation.

Correction de l'exercice 2 (4 points)

Probabilités

Exercice 2 4 points

Probabilités

Les parties A et B sont indépendantes. Dans cet exercice, toutes les probabilités demandées seront arrondies à $10^{-3}$.
Une usine métallurgique fabrique des boîtes de conserve pour des entreprises spécialisées dans le conditionnement industriel de légumes. La probabilité qu'une boîte prélevée au hasard soit non conforme est 0,04. Un lot de 200 boîtes choisies au hasard est livré à une entreprise spécialisée dans le conditionnement des légumes. Le nombre de boîtes fabriquées par cette usine métallurgique est assez important pour pouvoir assimiler un tel prélèvement à un tirage avec remise de 200 boîtes.

Partie A

La variable aléatoire $X$ désigne le nombre de boîtes non conformes dans un tel lot.

1. Justifier que la variable aléatoire $X$ suit une loi binomiale dont on précisera les paramètres.
Le nombre de boîtes est assez important pour pouvoir assimiler un tel prélèvement à un tirage avec remise de 200 boîtes par conséquent, la variable aléatoire $X$ suit une loi binomiale de paramètres $n=200$ et $p=0,04$ .
2. Déterminer la probabilité qu'un tel lot contienne exactement quatre boîtes non conformes.

2ND DISTR 0binomFdP( \1 , \2,\3)EXE
Avec une calculatrice de type TI $binomFdP(\1,\2,\3) \approx \4$

$$P( \5 = \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
La probabilité qu'un lot contienne exactement quatre boîtes non conformes est 0,055.

Partie B

On décide d'approcher la loi binomiale suivie par $X$ par la loi normale d'espérance $\mu = 8$ et d'écart type $\sigma = 2,77$.

1. Justifier le choix de ces paramètres.
La variable aléatoire X suit une loi binomiale de paramètres n=200 et p=0,04 alors :
• son espérance vaut $E(X)==n\times p= 200\times 0,04=8$ ;
• son écart-type vaut $\sigma =\sqrt{n\times p\times q}= \sqrt{200\times 0,04\times 0,96}\approx 2,77$.
En outre, on a $n=200, n⁢p=200\times 0,04=8$ et $n⁢(1-p)=200\times 0,96=192$.
Donc les trois conditions $n\geq 30, n⁢p\geq 5$ et $n⁢(1-p)\geq 5$ sont réunies pour approcher la loi binomiale par la loi normale.

La loi binomiale suivie par $X$ peut être approchée par la loi normale d'espérance $\mu=8$ et d'écart-type $\sigma=2,77$.
2. À l'aide de la loi normale ainsi définie :
   1. calculer $P(6 \leqslant X \leqslant 10)$ et interpréter le résultat trouvé ;

   2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
   Avec une calculatrice de type TI

   $$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$

   $$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$

    

   La probabilité qu'un lot contienne entre 6 et 10 boîtes non conformes est 0,53.
   2. déterminer une approximation de la probabilité qu'il y ait au maximum 4 boîtes non conformes.

   2ND DISTR 2NORMALFRép( -10^(99) , \1,$\2$,$\3$)EXE
   Avec une calculatrice de type TI

   $$NormalFR\text{é}p(-10^{99},\1,\2,\3) \approx \4$$

   $$P( \5 \leq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
   La probabilité qu'il y ait au maximum 4 boîtes non conformes est 0,074.

Partie C

La frequence de boîtes non conformes dans l'échantillon prélevé est $f=\frac{11}{200}=0,055$.

La proportion $p$ est égale à  $\1$. La taille  $n$  de l'échantillon considéré est égale à  $\2.$
Comme  $ n =\2$ ,   $n \times p  $=\3  et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.

L'intervalle de fluctuation asymptotique au seuil de  $95\% $  est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$ 

Exercice 3 3 points

QCM

Pour chacune des 3 propositions suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse. Il est attribué un point par réponse exacte correctement justifiée. Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.Indiquer sur la copie le numéro de la proposition, la réponse correspondante et la justification.

1. Proposition 1 : $e^{\mathrm{i}\frac{\pi}4{}}+e^{\mathrm{i}\frac{3\pi}4{}}=\mathrm{i}\sqrt{2}$.
2. La durée de vie, en heures, d'un composant électronique est une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $\lambda = 5,5 \times 10^{-4}$ et dont la fonction de densité de probabilité est représentée ci-dessous.
   
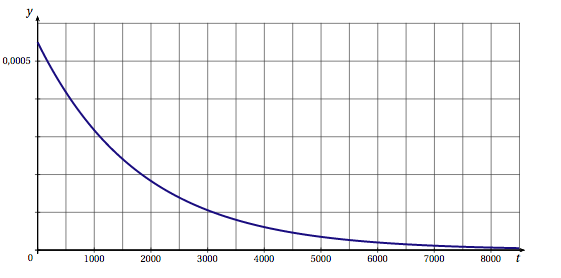
   Proposition 2 : la probabilité, arrondie à 0,01 près, qu'un composant électronique pris au hasard ait une durée de vie inférieure à 1000 heures est 0,35.
3. Proposition 3 : la valeur moyenne de la fonction $f$ définie sur l'intervalle $\left[\dfrac{\pi}{2} ; \pi\right]$ par $f (x) = \cos(x)$ est $-\dfrac{2}{\pi}$.
   On rappelle que la valeur moyenne $\mu$d'une fonction $f$ définie et continue sur un intervalle $[a ; b]$ est donnée par la formule :\[\mu = \dfrac{1}{b-a}\displaystyle\int_{a}^{b}f(x)\mathrm{d} x.\]

Correction de l'exercice 3 (3 points)

QCM

Pour chacune des 3 propositions suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse. Il est attribué un point par réponse exacte correctement justifiée. Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.Indiquer sur la copie le numéro de la proposition, la réponse correspondante et la justification.

1. Proposition 1 : $e^{\mathrm{i}\frac{\pi}4{}}+e^{\mathrm{i}\frac{3\pi}4{}}=\mathrm{i}\sqrt{2}$.
$$\begin{array}{rl} e^{\mathrm{i}\frac{\pi}4{}}+e^{\mathrm{i}\frac{3\pi}4{}}&= \cos\left ( \frac{\pi}4{} \right ) + \mathrm{i} \sin\left ( \frac{\pi}4{} \right )+ \cos\left ( \frac{3\pi}4{} \right ) + \mathrm{i} \sin\left ( 3\frac{\pi}4{} \right ) \\ &= \dfrac{\sqrt 2 }{2} + \mathrm{i} \dfrac{\sqrt 2 }{2}-\dfrac{\sqrt 2 }{2} + \mathrm{i} \dfrac{\sqrt 2 }{2}\\ &=\mathrm{i}\sqrt 2 \end{array}$$ La proposition 1 est vraie.
2. La durée de vie, en heures, d'un composant électronique est une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $\lambda = 5,5 \times 10^{-4}$ et dont la fonction de densité de probabilité est représentée ci-dessous.
   
   Proposition 2 : la probabilité, arrondie à 0,01 près, qu'un composant électronique pris au hasard ait une durée de vie inférieure à 1000 heures est 0,35.
La variable aléatoire $T$ suit la loi exponentielle de paramètre $\lambda =5,5\times 10^{-4}$ d'où : $$\begin{array}{rl} P(T\leq 1000 ) &= \displaystyle \int_0^{10200}\lambda\text{e}^{-\lambda t}\;\text{d}t \\ &= \left [ -\text{e}^{-\lambda t}\right ]_0^{1000}\\ &=-\text{e}^{-1000 \lambda }-\left (-\text{e}^{0}\right )\\ &= 1- \text{e}^{-1000 \times 5,5\times 10^{-4} }\\ &= 1-\text{e}^{-0,55 }\\ &\approx 0, 423 \end{array}$$ La proposition 2 est fausse.
3. Proposition 3 : la valeur moyenne de la fonction $f$ définie sur l'intervalle $\left[\dfrac{\pi}{2} ; \pi\right]$ par $f (x) = \cos(x)$ est $-\dfrac{2}{\pi}$.
   On rappelle que la valeur moyenne $\mu$d'une fonction $f$ définie et continue sur un intervalle $[a ; b]$ est donnée par la formule :\[\mu = \dfrac{1}{b-a}\displaystyle\int_{a}^{b}f(x)\mathrm{d} x.\]
La valeur moyenne de la fonction $f$ définie sur l'intervalle $\left[\dfrac{\pi}{2} ; \pi\right]$ par $f (x) = \cos(x)$ est : $$\begin{array}{rl} \mu &= \dfrac{1}{\pi -\dfrac{\pi}{2}}\displaystyle\int_{\dfrac{\pi}{2}}^{\pi }\cos x \mathrm{d} x \\ &= \left [ \sin x \right ]_{\dfrac{\pi}{2}} ^{\pi }\\ &=\dfrac{2}{\pi }\left ( \sin \pi-\sin\left (\dfrac{\pi}{2}\right )\right )\\ &= \dfrac{2}{\pi } ( 0-1)\\ &=- \dfrac{2}{\pi } \end{array}$$ La proposition 3 est vraie.

Exercice 4 7 points

Suites

Les parties A, B et C sont indépendantes.
Dans une municipalité, la collecte des déchets des particuliers s'effectue, depuis 2012, à l'aide de camions équipés de capteurs. Une tarification « incitative » permet aux habitations de diminuer leur facture en réduisant la masse de leurs ordures ménagères résiduelles par un choix de produits comportant moins d'emballages, une réduction du gaspillage alimentaire et un meilleur tri. Le document 1 présente la masse moyenne de déchets, en kilogrammes, collectés par année depuis 2012 et par habitation de la ville. Le document 2 présente les tarifs pratiqués en 2015 par la ville pour la collecte des ordures ménagères résiduelles (on suppose que ces tarifs resteront identiques les années suivantes).

Document 1

Années 2012 à 2015

$$\begin{array} {|c| c|c|c|c|} \hline \text{Année} &\text{2012} & \text{2013} & \text{2014} & \text{2015}\\ \hline \text{Déchets recyclables} & 261 & 275 & 289 & 305\\ \hline \text{Ordures ménagères résiduelles} & 274 & 269 & 262 & 256\\ \hline \text{Total} & 535 & 544 & 551 & 561\\ \hline \end{array}$$

Document 2

Année 2015

$$\begin{array}{|c| c|c|c|} \hline \text{Tranches } \text{tarifaires} & \text{Tranche 1} & \text{Tranche 2} & \text{Tranche 3}\\ \hline \text{Masse M en} \text{kilogrammes} & 0 \leqslant M < 100 & 100 \leqslant M < 300 & 300 \leqslant M \\ \hline \text{Forfait} & 200 € & 300 € & 420 €\\ \hline \end{array} $$

Partie A

1. Commenter l'évolution de la masse moyenne des déchets collectés par habitation depuis 2012.
2. Une famille a jeté 320 kg d'ordures ménagères résiduelles en 2015. Si elle diminue la masse de ses ordures ménagères résiduelles de 1 % par an, en quelle année changera-t-elle de tranche tarifaire ?

Partie B

En 2015, la municipalité comptait 10000 habitations. Dans le cadre de l'aménagement d'un nouveau quartier un constructeur garantit la livraison de 300 nouvelles habitations chaque année au 1er janvier, de 2016 à 2024. En raison de la demande, ces logements seront immédiatement occupés dès le 1er janvier. La municipalité a souscrit avec un centre d'incinération un contrat de 9 ans qui a pris effet au 1er janvier 2016. Le contrat prévoit de fortes pénalités financières dès que la masse annuelle d'ordures ménagères résiduelles à incinérer vient à dépasser 2800 tonnes. L'objectif de la municipalité est d'éviter ces pénalités.

1. Vérifier que cet objectif ne sera pas atteint si la masse annuelle moyenne d'ordures ménagères résiduelles par habitation reste constante égale à 256 kg.
2. Afin d'atteindre cet objectif, il convient donc de diminuer la masse moyenne d'ordures ménagères résiduelles à incinérer. La municipalité souhaite déterminer le pourcentage annuel minimal de réduction de la masse moyenne d'ordures ménagères résiduelles par habitation, pendant toute la durée du contrat. On admet que l'algorithme ci-dessous détermine ce pourcentage.
   Variables
   • $N$ : un nombre entier
   • $m$ : un nombre réel
   • $q$ : un nombre réel
   Initialisation
   • $q$ prend la valeur 1
   • $N$ prend la valeur 12700
   • $m$ prend la valeur 0,256
   Traitement
   • Tant que $N \times m \geqslant 2800$
     $q$ prend la valeur $q-0,001$
     $m$ prend la valeur $0,256 \times q^9$
   • Fin Tant que
   Sortie Afficher $\left(1-q\right) \times 100$
Cet algorithme affiche 1,7.
1. Expliquer la ligne « $N$ prend la valeur 12700 »
2. Expliquer la ligne « $m$ prend la valeur $0,256 \times q^9$ »
3. On considère que la masse annuelle moyenne d'ordures ménagères résiduelles par habitation va baisser chaque année de 1,7 %, à partir du 1\up{er} janvier 2016 sur une période de 9 ans. On note $u_n$ cette masse, exprimée en tonnes, pour l'année $2015 + n$ où $n$ est un entier naturel. On a donc $u_0 = 0,256$.
   1. Calculer les termes $u_1$, $u_2$ et vérifier que $u_3\approx 0,243$. Interpréter $u_3$.
   2. Quelle est la nature de la suite $\left(u_n\right)$ ?
   3. Exprimer $u_n$ en fonction de $n$.
   4. Vérifier que l'objectif fixé par la municipalité est atteint en fin de 2024.

Partie C

Dans cette partie, tous les résultats demandés seront arrondis à $10^{-3}$. Des contrôles sont effectués afin de vérifier le tri des déchets.

Protocole d'étude

On choisit au hasard $100$ habitations. Des personnels ont ouvert les poubelles de déchets recyclables de ces habitations afin de déterminer s'ils étaient conformes (absence de matériaux non recyclables, de cartons souillés $\ldots$).

Résultats de l'étude

Parmi ces 100 poubelles de déchets recyclables, 7 ont été jugées non conformes.

1. Déterminer, à l'aide d'un intervalle de confiance avec un niveau de confiance de 95 %, une estimation de la proportion de poubelles de déchets recyclables qui ne sont pas conformes.
2. La proportion de poubelles de déchets recyclables qui ne sont pas conformes est-elle nécessairement comprise dans cet intervalle de confiance ?

Exercice 4 7 points

Suites

Les parties A, B et C sont indépendantes.
Dans une municipalité, la collecte des déchets des particuliers s'effectue, depuis 2012, à l'aide de camions équipés de capteurs. Une tarification « incitative » permet aux habitations de diminuer leur facture en réduisant la masse de leurs ordures ménagères résiduelles par un choix de produits comportant moins d'emballages, une réduction du gaspillage alimentaire et un meilleur tri. Le document 1 présente la masse moyenne de déchets, en kilogrammes, collectés par année depuis 2012 et par habitation de la ville. Le document 2 présente les tarifs pratiqués en 2015 par la ville pour la collecte des ordures ménagères résiduelles (on suppose que ces tarifs resteront identiques les années suivantes).

Document 1

Années 2012 à 2015

$$\begin{array} {|c| c|c|c|c|} \hline \text{Année} &\text{2012} & \text{2013} & \text{2014} & \text{2015}\\ \hline \text{Déchets recyclables} & 261 & 275 & 289 & 305\\ \hline \text{Ordures ménagères résiduelles} & 274 & 269 & 262 & 256\\ \hline \text{Total} & 535 & 544 & 551 & 561\\ \hline \end{array}$$

Document 2

Année 2015

$$\begin{array}{|c| c|c|c|} \hline \text{Tranches } \text{tarifaires} & \text{Tranche 1} & \text{Tranche 2} & \text{Tranche 3}\\ \hline \text{Masse M en} \text{kilogrammes} & 0 \leqslant M < 100 & 100 \leqslant M < 300 & 300 \leqslant M \\ \hline \text{Forfait} & 200 € & 300 € & 420 €\\ \hline \end{array} $$

Partie A

1. Commenter l'évolution de la masse moyenne des déchets collectés par habitation depuis 2012.
Soit t % le pourcentage d'augmentation annuel moyen de la masse des déchets collectés par habitation de 2012 à 2015. On a : $$\begin{array}{rl} 535\times \left(1+\dfrac{t}{100} \right)^3= 561& \iff \left(1+\dfrac{t}{100} \right)^3 = \dfrac{561}{535} \\ & \left(1+\dfrac{t}{100} \right) = \left(\dfrac{561}{535} \right)^{\frac{1}{3}}\\ &\iff \dfrac{t}{100} \approx 0,0159 \end{array}$$ Depuis 2012, la masse moyenne des déchets collectés par habitation a augmenté d'envirion 1,6 % par an.

2. Une famille a jeté 320 kg d'ordures ménagères résiduelles en 2015. Si elle diminue la masse de ses ordures ménagères résiduelles de 1 % par an, en quelle année changera-t-elle de tranche tarifaire ?
Soit $n$ le nombre d'années nécessaires pour passer dans la tranche 2. $n$ est le plus petit entier solution de l'inéquation : $$\begin{array}{rll} 320\times 0,99^n< 300 & \iff 0,99^n < \dfrac{300}{320}&\\ & \iff \ln\left (0,99^n\right ) \leqslant \ln\left (\dfrac{15}{16}\right ) & \text{ car } \ln \text{ est strictement croissante } \\ && \text{ sur } ]0; +\infty[ \\ &\iff n \ln\left (0,9 \right ) \leqslant\ln\left (\dfrac{15}{16}\right ) & \text{ car } \ln\left (a^n\right )=n\ln a \\ &\iff n\geq \dfrac{\ln\left (\dfrac{15}{16}\right )}{\ln\left (0,99 \right )}& \text{ car } 0,99< 1 \text{ ainsi } \ln\left (0,9 \right )< 0\\ \end{array}$$ Comme $\dfrac{\ln\left (\dfrac{15}{16}\right )}{\ln\left (0,99 \right )}\approx 6,4$ on en déduit que $n=7$ Si cette famille diminue la masse de ses ordures ménagères résiduelles de 1 % par an, c'est en 2022 qu'elle changera de tranche tarifaire.

Partie B

En 2015, la municipalité comptait 10000 habitations. Dans le cadre de l'aménagement d'un nouveau quartier un constructeur garantit la livraison de 300 nouvelles habitations chaque année au 1er janvier, de 2016 à 2024. En raison de la demande, ces logements seront immédiatement occupés dès le 1er janvier. La municipalité a souscrit avec un centre d'incinération un contrat de 9 ans qui a pris effet au 1er janvier 2016. Le contrat prévoit de fortes pénalités financières dès que la masse annuelle d'ordures ménagères résiduelles à incinérer vient à dépasser 2800 tonnes. L'objectif de la municipalité est d'éviter ces pénalités.

1. Vérifier que cet objectif ne sera pas atteint si la masse annuelle moyenne d'ordures ménagères résiduelles par habitation reste constante égale à 256 kg.
Soit $a_n$ le nombre d'habitations le 1er janvier de l'année $2015+n$.
On a $a_0=10000$ et, pour tout entier $n, a_{n+1}=a_n+300$.
La suite $(a_n)$ est une suite arithmétique de premier terme $a_0=10000$ et de raison $r=300$. Donc pour tout entier $n$, on a $a_n=10000+300\times n$.
La masse d'ordures ménagères résiduelles à incinérer , exprimée en tonnes, pour l'année $2015+n$ est $d_n=a_n\times 0,256$.
Soit pour tout entier $n, d_n=10000+300\times n\times 0,256=2560+76,8\times n$
Donc : $$\begin{array}{rl} d_n \leq 2800 &\iff 2560+76,8\times n\leq 2800 \\ &\iff 76,8\times n\leq 2800 \\ &\iff n\leq \dfrac{240}{76,8}\\ &\iff n\leq 3,125 \end{array}$$ Si la masse annuelle moyenne d'ordures ménagères résiduelles par habitation reste constante égale à 256 kg, l'objectif ne sera pas atteint dès la quatrième année c'est à dire au 1er janvier 2019.
2. Afin d'atteindre cet objectif, il convient donc de diminuer la masse moyenne d'ordures ménagères résiduelles à incinérer. La municipalité souhaite déterminer le pourcentage annuel minimal de réduction de la masse moyenne d'ordures ménagères résiduelles par habitation, pendant toute la durée du contrat. On admet que l'algorithme ci-dessous détermine ce pourcentage.
   Variables
   • $N$ : un nombre entier
   • $m$ : un nombre réel
   • $q$ : un nombre réel
   Initialisation
   • $q$ prend la valeur 1
   • $N$ prend la valeur 12700
   • $m$ prend la valeur 0,256
   Traitement
   • Tant que $N \times m \geqslant 2800$
     $q$ prend la valeur $q-0,001$
     $m$ prend la valeur $0,256 \times q^9$
   • Fin Tant que
   Sortie Afficher $\left(1-q\right) \times 100$
Cet algorithme affiche 1,7.
1. Expliquer la ligne « $N$ prend la valeur 12700 »
Le nombre d'habitations en 2024 est : $$a_9=10000+300\times 9=12700$$ $N=12700$ modélise le nombre d'habitations en 2024.
2. Expliquer la ligne « $m$ prend la valeur $0,256 \times q^9$ »
Le coefficient multiplicateur associé à une baisse annuelle de $t\; \%$ de la masse d'ordures ménagères résiduelles par habitation est : $q=1-\dfrac{t}{100}$
Au bout de 9 ans, la masse annuelle moyenne d'ordures ménagères résiduelles par habitation, exprimée en tonnes, est donc $m=0,256\times q^9$
3. On considère que la masse annuelle moyenne d'ordures ménagères résiduelles par habitation va baisser chaque année de 1,7\%, à partir du 1\up{er} janvier 2016 sur une période de 9 ans. On note $u_n$ cette masse, exprimée en tonnes, pour l'année $2015 + n$ où $n$ est un entier naturel. On a donc $u_0 = 0,256$.
   1. Calculer les termes $u_1$, $u_2$ et vérifier que $u_3\approx 0,243$. Interpréter $u_3$.
   Le coefficient multiplicateur associé à une baisse annuelle de $1,7\;\ %$ de la masse d'ordures ménagères résiduelles par habitation est : $q=1-\dfrac{1,7}{100}=0,983$ On en déduit que :
   • $u_1=0,256\times 0,983\approx 0,243$
   • $u_2=0,256\times 0,9832\approx 0,247$
   • $u_3=0,256\times 0,9833\approx 0,243$
   Fin 2018 ( ou au 1er janvier 2019), la masse annuelle moyenne d'ordures ménagères résiduelles par habitation est d'environ 243 kg.
   2. Quelle est la nature de la suite $\left(u_n\right)$ ?
   Pour tout entier $n, u_{n+1}=u_n\times 0,983$ donc $(u_n)$ est une suite géométrique de raison $q=0,983$.
   3. Exprimer $u_n$ en fonction de $n$.
   $(u_n)$ est une suite géométrique de raison $q=0,983$ et de premier terme $u_0=0,256$ donc pour tout entier $n$, on a $u_n=0,256\times 0,983^n.$
   4. Vérifier que l'objectif fixé par la municipalité est atteint en fin de 2024.
   À la fin de l'année 2024, le nombre d'habitations est de 12700 et la masse annuelle moyenne d'ordures ménagères résiduelles par habitation est $m=0,256\times 0,9839$.
   Par conséquent, la masse totale d'ordures ménagères résiduelles est : $$12700\times 0,256\times 0,9839\approx 27986,3$$ L'objectif fixé par la municipalité est atteint en fin de 2024.

Partie C

Dans cette partie, tous les résultats demandés seront arrondis à $10^{-3}$. Des contrôles sont effectués afin de vérifier le tri des déchets.

Protocole d'étude

On choisit au hasard $100$ habitations. Des personnels ont ouvert les poubelles de déchets recyclables de ces habitations afin de déterminer s'ils étaient conformes (absence de matériaux non recyclables, de cartons souillés $\ldots$).

Résultats de l'étude

Parmi ces 100 poubelles de déchets recyclables, 7 ont été jugées non conformes.

1. Déterminer, à l'aide d'un intervalle de confiance avec un niveau de confiance de 95 %, une estimation de la proportion de poubelles de déchets recyclables qui ne sont pas conformes.

La fréquence est égale à  $\1$. La taille $n$ de l'échantillon considéré est égale à  $\2.$
Comme  $ n =\2$ ,   $n \times \8  $=\3  et $n\times (1-\8)=\4,$ les conditions d'utilisation d'un intervalle de confiance sont réunies.

En effet on a bien : $$n \geq 30\;;\; n \times \8 \geq 5 \text{ et } n\times (1-\8) \geq 5$$

L' intervalle de confiance avec un niveau de confiance de 95% est : \[\9 = \left[\8 - 1,96\sqrt{\dfrac{\8(1 - \8)}{n}}~;~\8 + 1,96\sqrt{\dfrac{\8(1 - \8)}{n}} \right]\]
La fréquence est $\8=\1$.
L'intervalle de confiance au niveau de 95% est \[\9 = \left[\1 - 1,96\sqrt{\dfrac{\1 (1 - \1 )}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1 (1 - \1 )}{\2}} \right]\approx[\5~;~\6]\] 

Soit avec des valeurs approchées à $10^{-3}$ près des bornes de l'intervalle, l'intervalle de confiance est $IC_{100}=[0,019; 0,12]$.
2. La proportion de poubelles de déchets recyclables qui ne sont pas conformes est-elle nécessairement comprise dans cet intervalle de confiance ?
Un intervalle de confiance avec un niveau de confiance de 95 % ne contient pas nécessairement la propotion $p$ inconnue. Si on extrait un gand nombre d'échantillons de même taille, 95 % des échantillons donnent un intervalle de confiance contenant $p$.
La proportion de poubelles de déchets recyclables qui ne sont pas conformes n'appartient pas nécessairement à cet intervalle de confiance.