Baccalauréat STI2D NOUVELLE CALÉDONIE 2013

Exercice 1 5 points

Suites

La suite $\left(u_{n}\right)$ est définie pour tout entier naturel $n$ par $u_{n+1} = 0,4u_{n} + 3$ et $u_{0} = - 1$.

---

Partie A

---

1. À l'aide d'un tableur, on a calculé les 11 premières valeurs de $u_{n}$. On obtient les résultats suivants : $$\begin{array}{ }\hline & A &B &C &D &E &F &G &H &I &J &K &L\\ \hline 1&\text{ Valeur de } n&0&1&2&3&4&5&6&7&8&9&10\\ \hline 2&\text{Valeur de }u_n& - 1& 2,6 & 4,04 & 4,616 & 4,8464 & 4,9386 & 4,9754 & 4,9902 & 4,9961 & 4,9984 & 4,9994 \\ \hline \end{array}$$ Parmi les quatre formules ci-dessous, laquelle a-t-on entré dans la cellule C2 pour obtenir par copie vers la droite les valeurs affichées dans les cellules D2 à L2 (on indiquera la réponse sur la copie sans justification) ?

   a. = 0,4^n +3

   b. = $ B$ 2*0,4+3

   c. =B2*0,4+3

   d.= 0,4 ^ C 1+3

2. Quelle conjecture peut-on faire sur la limite de la suite $\left(u_{n}\right)$ ?
3. On considère l'algorithme suivant : $$\begin{array}{|l l|}\hline \text{variables :} & p \text{ et } n \text{ sont des entiers naturels,} \\ & u \text{ est un nombre réel }\\ \text{\entrée :} & \text{ saisir la valeur de } p \\ \text{initialisation :}& n \text{ prend la valeur } 0 , \\ & u \text{ prend la valeur } - 1 \\ \text{traitement :} & \text{ Tant que } |u - 5| > 10^{-p} \\ & \begin{array}{ |l} n \text{ prend la valeur } n + 1 \\ u \text{ prend la valeur } 0,4u + 3 \end{array}\\ & \text{ Fin Tant que }\\ \text{ sortie :} & \text{Afficher la valeur de } n \\ \hline \end{array} $$ À l'aide du tableau de la question 1, donner la valeur affichée par cet algorithme lorsque $p = 2$.

---

Partie B

---

On étudie maintenant la suite $\left(v_{n}\right)$ définie pour tout entier naturel $n$ par $v_{n} = 6 \times (0,4)^n$.

1. Donner la nature de la suite $\left(v_{n}\right)$ et ses éléments caractéristiques.
2. Déterminer la limite de $\left(v_{n}\right)$ quand $n$ tend vers $+ \infty$.
3. On admet que pour tout entier naturel $n$ : $u_{n} = 5 - v_{n}$. Déterminer la limite de $\left(u_{n}\right)$.
4. 1. Déterminer en fonction de $n$ la somme $v_{0} + v_{1} + \cdots + v_{n}$.
   2. En déduire en fonction de $n$ la somme $u_{0} + u_{1} + \cdots + u_{n}$.

 

Correction de l'exercice 1 (5 points)

Suites

La suite $\left(u_{n}\right)$ est définie pour tout entier naturel $n$ par $u_{n+1} = 0,4u_{n} + 3$ et $u_{0} = - 1$.

---

Partie A

---

1. À l'aide d'un tableur, on a calculé les 11 premières valeurs de $u_{n}$. On obtient les résultats suivants : $$\begin{array}{ }\hline & A &B &C &D &E &F &G &H &I &J &K &L\\ \hline 1&\text{ Valeur de } n&0&1&2&3&4&5&6&7&8&9&10\\ \hline 2&\text{Valeur de }u_n& - 1& 2,6 & 4,04 & 4,616 & 4,8464 & 4,9386 & 4,9754 & 4,9902 & 4,9961 & 4,9984 & 4,9994 \\ \hline \end{array}$$ Parmi les quatre formules ci-dessous, laquelle a-t-on entré dans la cellule C2 pour obtenir par copie vers la droite les valeurs affichées dans les cellules D2 à L2 (on indiquera la réponse sur la copie sans justification) ?

   a. = 0,4^n +3

   b. = $ B$ 2*0,4+3

   c. =B2*0,4+3

   d.= 0,4 ^ C 1+3

Réponse c. : =B2*0,4+3
2. Quelle conjecture peut-on faire sur la limite de la suite $\left(u_{n}\right)$ ?
Il semble que la limite de la suite soit égale à $5$.
3. On considère l'algorithme suivant : $$\begin{array}{|l l|}\hline \text{variables :} & p \text{ et } n \text{ sont des entiers naturels,} \\ & u \text{ est un nombre réel }\\ \text{\entrée :} & \text{ saisir la valeur de } p \\ \text{initialisation :}& n \text{ prend la valeur } 0 , \\ & u \text{ prend la valeur } - 1 \\ \text{traitement :} & \text{ Tant que } |u - 5| > 10^{-p} \\ & \begin{array}{ |l} n \text{ prend la valeur } n + 1 \\ u \text{ prend la valeur } 0,4u + 3 \end{array}\\ & \text{ Fin Tant que }\\ \text{ sortie :} & \text{Afficher la valeur de } n \\ \hline \end{array} $$ À l'aide du tableau de la question 1, donner la valeur affichée par cet algorithme lorsque $p = 2$.
L'algorithme s'arrête pour $p = 7$ : avec $u_{7}= 4,9902 $, on a bien $\left|u_{7} - 5 \right| \leqslant 0,01$.

---

Partie B

---

On étudie maintenant la suite $\left(v_{n}\right)$ définie pour tout entier naturel $n$ par $v_{n} = 6 \times (0,4)^n$.

1. Donner la nature de la suite $\left(v_{n}\right)$ et ses éléments caractéristiques.
D'après l'écriture du terme général $v_{n} = v_0 \times q^n$, cette suite est géométrique de premier terme $6$ et de raison $0,4$.
2. Déterminer la limite de $\left(v_{n}\right)$ quand $n$ tend vers $+ \infty$.
Comme $0 < 0,4 < 1$, on sait que $\displaystyle\lim_{n \to + \infty} 0,4^n = 0$, donc $\displaystyle\lim_{n \to + \infty} 6 \times 0,4^n = 0$. Conclusion : $\displaystyle\lim_{n \to + \infty} v_{n} = 0$.
3. On admet que pour tout entier naturel $n$ : $u_{n} = 5 - v_{n}$. Déterminer la limite de $\left(u_{n}\right)$.
Comme $u_{n} = 5 - v_{n}$, on en déduit que $\displaystyle\lim_{n \to + \infty} u_{n} = 5 - 0 = 5$.
4. 1. Déterminer en fonction de $n$ la somme $v_{0} + v_{1} + \cdots + v_{n}$.
   Cette somme est la somme des $(n + 1)$ premiers termes d'une suite géométrique, on sait que cette somme est égale à : $$\begin{array}{rl}v_{0} + v_{1} + \cdots + v_{n}&= \dfrac{1 - \text{Raison}^{\text{Nombres de termes}}}{1 - \text{Raison}}\times \text{Premier Terme}\\ &= \dfrac{1 - 0,4^{n+1}}{1 - 0,4}\times 6\\ &= 6 \times \dfrac{1 - 0,4^{n+1}}{0,6}\\&= 10 \left(1 - 0,4^{n+1} \right) \\ &= 10 - 4 \times 0,4^n. \end{array}$$
   2. En déduire en fonction de $n$ la somme $u_{0} + u_{1} + \cdots + u_{n}$.
   Comme pour tout entier $n, \: u_{n} = 5 - v_{n}$, on a : $$\begin{array}{rl} u_{0} + u_{1} + \cdots + u_{n} &= 5 - v_{0}+5 - v_{1 } +\cdots +5 - v_{n}\\ &= 5 (n + 1) - \left(v_{0} + v_{1} + \cdots + v_{n}\right)\\ &= 5 (n + 1) - \left(10 - 4 \times 0,4^n \right) \\ &= 5n + 5 - 10 + 4\times 0,4^n \\ &= 5n - 5 + 4\times 0,4^n\\ &=5(n - 1) + 4\times 0,4^n \end{array}$$.

Exercice 2 3 points

QCM

Cet exercice est un questionnaire à choix multiples. Pour chaque question, une seule réponse est correcte.
$\mathbb R$ désigne l'ensemble des nombres réels.
Toute bonne réponse rapporte $0,5$ point. Une réponse erronée ou l'absence de réponse n'enlève ni ne rapporte aucun point. Aucune justification n'est demandée.
Le candidat notera le numéro de la question et la lettre correspondante à la réponse choisie sur sa copie.

1. Soit $z = - \sqrt{2}e^{\mathrm{i}\frac{\pi}{4}}$. Alors son module est :
   1. $\sqrt{2}$
   2. $- \sqrt{2}$
   3. $2$
2. Soit $z = - \sqrt{2}e^{\mathrm{i}\frac{\pi}{4}}$. Alors un argument est :
   1. $\dfrac{\pi}{4}$
   2. $- \dfrac{\pi}{4}$
   3. $- \dfrac{3\pi}{4}$
3. $f$ est définie par $f (t) = 3\cos \left(5 t - \dfrac{\pi}{2}\right)$
   1. $f$ est solution de : & $y' + 3y = 0$
   2. $y''+ 25y = 0$
   3. $y'' - 5y = 0$
4. Les solutions de l'équation $y' - 2y = 0$ sont les fonctions du type :
   1. $x \mapsto ke^{2x}$ avec $k \in \mathbb R$
   2. $x \mapsto ke^{- 2x}$ avec $k \in \mathbb R$
   3. $x \mapsto ke^{2x} + k$ avec $k \in \mathbb R$
5. La solution de l'équation $\ln (x + 1) = 3$ est :
   1. $\left\{1 - e^3\right\}$
   2. $\left\{1 + e^3\right\}$
   3. $\left\{e^3 - 1\right\}$
6. L'ensemble des solutions de l'inéquation $2^x - 3 \leqslant 5$ est :
   1. $]- \infty ; \ln 8]$
   2. $]- \infty ; 3]$
   3. $]- \ln 3 ; \ln 5]$

 

Correction de l'exercice 2 (3 points)

QCM

Cet exercice est un questionnaire à choix multiples. Pour chaque question, une seule réponse est correcte.
$\mathbb R$ désigne l'ensemble des nombres réels.
Toute bonne réponse rapporte $0,5$ point. Une réponse erronée ou l'absence de réponse n'enlève ni ne rapporte aucun point. Aucune justification n'est demandée.
Le candidat notera le numéro de la question et la lettre correspondante à la réponse choisie sur sa copie.

1. Soit $z = - \sqrt{2}e^{\mathrm{i}\frac{\pi}{4}}$. Alors son module est :
   1. $\sqrt{2}$
   2. $- \sqrt{2}$
   3. $2$
Réponse a.
2. Soit $z = - \sqrt{2}e^{\mathrm{i}\frac{\pi}{4}}$. Alors un argument est :
   1. $\dfrac{\pi}{4}$
   2. $- \dfrac{\pi}{4}$
   3. $- \dfrac{3\pi}{4}$
$z = - \sqrt{2}\text{e}^{\text{i}\frac{\pi}{4}}$ : cette écriture n'est pas celle d'une forme exponentielle car $ \sqrt{2} < 0$.
On utilise le fait que $ - 1= \text{e}^{\text{i}\pi}$
Or $z = \text{e}^{\text{i}\pi} \sqrt{2}\text{e}^{\text{i}\frac{\pi}{4}} = \sqrt{2}\text{e}^{\text{i}\left(\pi + \frac{\pi}{4}\right)} = \sqrt{2}\text{e}^{\text{i}\frac{5\pi}{4}}$ Un argument de $z$ est donc $\frac{5\pi}{4}$ à $2\pi$ près soit encore $- \frac{3\pi}{4}$.
Réponse c.
3. $f$ est définie par $f (t) = 3\cos \left(5 t - \dfrac{\pi}{2}\right)$
   1. $f$ est solution de : & $y' + 3y = 0$
   2. $y''+ 25y = 0$
   3. $y'' - 5y = 0$
Si $f$ est définie par $f(t) = 3\cos \left(5 t - \dfrac{\pi}{2}\right)$, alors $f'(t) = - 15 \sin \left(5 t - \dfrac{\pi}{2}\right)$ et $f''(t) = - 75 \cos \left(5 t - \dfrac{\pi}{2}\right)$.
Donc $f''(t) + 25f(t) = 0$.
Réponse b.
4. Les solutions de l'équation $y' - 2y = 0$ sont les fonctions du type :
   1. $x \mapsto ke^{2x}$ avec $k \in \mathbb R$
   2. $x \mapsto ke^{- 2x}$ avec $k \in \mathbb R$
   3. $x \mapsto ke^{2x} + k$ avec $k \in \mathbb R$
$y' - 2y = 0\iff y'=2y$, cette équation différentielle est de la forme $y'=ay$ où $a=2$.
Les solutions de l'équation différentielle sont les fonctions : $x \longmapsto C\text{e}^{2x}$ avec $C \in \mathbb R$.
Réponse a.
5. La solution de l'équation $\ln (x + 1) = 3$ est :
   1. $\left\{1 - e^3\right\}$
   2. $\left\{1 + e^3\right\}$
   3. $\left\{e^3 - 1\right\}$
$$\begin{array}{rl} \ln (x + 1) = 3 &\iff \text{e}^{\ln (x + 1)} = \text{e}^{3} \\ &\iff x + 1 = \text{e}^{3} \\ & \iff x = \text{e}^{3} - 1\end{array}$$
Réponse c.
6. L'ensemble des solutions de l'inéquation $2^x - 3 \leqslant 5$ est :
   1. $]- \infty ; \ln 8]$
   2. $]- \infty ; 3]$
   3. $]- \ln 3 ; \ln 5]$
   $$\begin{array}{rl} 2^x - 3 \leqslant 5 &\iff 2^x \leqslant 8 \\ & \iff x\ln 2 \leqslant \ln 8\\ & \iff x\ln 2 \leqslant \ln 2^3 \\ & \iff x \ln 2 \leqslant 3 \ln 2 \\ &\iff x \leqslant 3\end{array}$$
   Réponse b.

 

Exercice 3 7 points

Fonctions logarithmes

Partie A

---

$f$ est une fonction définie et dérivable sur l'intervalle $]0 ; +\infty[$. $f'$ désigne la fonction dérivée de $f$.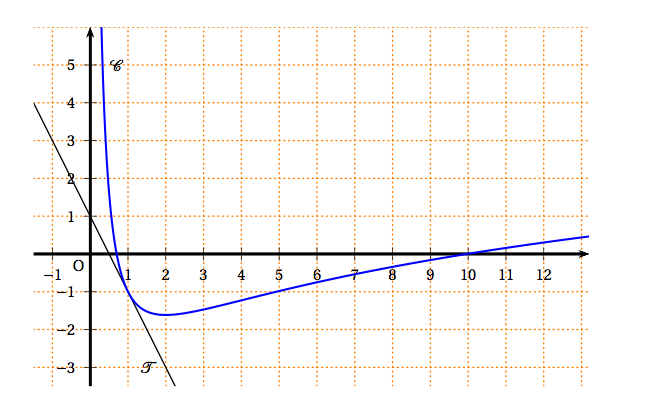

• $\mathcal{C}$ est la représentation graphique de la fonction $f$ dans un repère orthonormal.
• $T$ est la tangente à $\mathcal{C}$ au point de coordonnées $(1 ; -1)$. $T$ passe par le point de coordonnées $(0;1)$.

---

1. 1. Par lecture graphique, déterminer $f(1)$.
   2. Déterminer $f'(1)$.
   3. Donner une équation de $T$.
2. On sait que $f(x)$ est de la forme $f(x) = 2\ln x+ \dfrac{a}{x} + b$ où $a$ et $b$ sont des nombres réels.
   1. Calculer $f'(x)$.
   2. Déterminer alors les valeurs de $a$ et $b$.

---

Partie B

---

Soit la fonction $f$ définie et dérivable sur $]0 ; +\infty[$ par $f(x) = 2\ln x + \dfrac{4}{x} - 5$.

1. 1. Déterminer $\displaystyle\lim_{x \to + \infty} f(x)$.
   2. On admet que $\displaystyle\lim_{x \to 0} f(x) = + \infty$. Que peut-on en déduire graphiquement ?
2. 1. Pour tout nombre réel $x$ appartenant à $]0 ; +\infty[$, vérifier que $f'(x) = \dfrac{2x - 4}{x^2}$.
   2. Étudier le signe de $f'(x)$ sur $]0 ; +\infty[$.
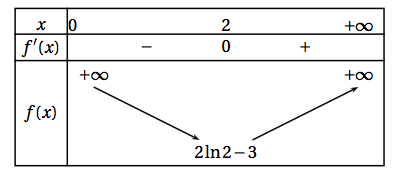
3. Établir le tableau de variations de $f$ sur $]0 ; +\infty[$.
4. En précisant votre démarche, donner le nombre de solution(s) de l'équation $f(x) = 0$, pour $x$ appartenant à $]0 ; +\infty[$.
5. 1. Donner le signe de $f(x)$ pour $x$ appartenant à $[1 ; 3]$.
   2. On admet que la fonction $F$ définie pour $x$ appartenant à $]0 ; +\infty[$ par $F(x) = (2x + 4) \ln x - 7x$ est une primitive de $f$. Déterminer l'aire $\mathcal{A}$ du domaine limité par la courbe $\mathcal{C}$, l'axe des abscisses et les droites d'équation $x = 1$ et $x = 3$ en unités d'aires. On donnera la valeur exacte puis une valeur approchée à $10^{-2}$ près de $\mathcal{A}$.

 

Correction de l'exercice 3 (7 points)

Fonctions logarithmes

Partie A

---

$f$ est une fonction définie et dérivable sur l'intervalle $]0 ; +\infty[$. $f'$ désigne la fonction dérivée de $f$.

• $\mathcal{C}$ est la représentation graphique de la fonction $f$ dans un repère orthonormal.
• $T$ est la tangente à $\mathcal{C}$ au point de coordonnées $(1 ; -1)$. $T$ passe par le point de coordonnées $(0;1)$.

---

1. 1. Par lecture graphique, déterminer $f(1)$.
   On lit $f(1) \approx - 1$.
   $f(1)=- 1$.
   2. Déterminer $f'(1)$.
   $f'(1)$ est le coefficient directeur de la tagente $T$ à $\mathcal{C}$ au point de coordonnées $(1 ; -1)$.
   On lit $f'(1) = \dfrac{y_B-y_A}{x_B-x_A}=\dfrac{-2}{1} = - 2$.
   $f'(1)=- 2$.
   3. Donner une équation de $T$.
      • Méthode 1 : Son coefficient directeur est égal à $- 2$ et son ordonnée à l'origine 1 ; l'équation de $\mathcal{T}$ est donc $y = - 2x + 1$.
      • Méthode 2 :
        

        La tangente $\1$ à $\2$ au point d'abscisse $a= \3$ a pour équation : $$y=\6'(\3)(x-\3)+\6(\3)$$ Ici $a= \3$, on calcule successivement :

        • $\6\left(\3 \right)=\4$
        • $\6'\left (\3\right )=\5$

        Ainsi $\1:y=\5\left (x-\3\right )+\4$

        
        
        l'équation de $\mathcal{T}$ est donc $y = - 2x + 1$.
2. On sait que $f(x)$ est de la forme $f(x) = 2\ln x+ \dfrac{a}{x} + b$ où $a$ et $b$ sont des nombres réels.
   1. Calculer $f'(x)$.
   $f'(x) = 2\times\dfrac{1}{x} - \dfrac{a}{x^2} = \dfrac{2x - a}{x^2}$.
   2. Déterminer alors les valeurs de $a$ et $b$.
   On sait que $f'(1) = - 2$ soit $\dfrac{2\times 1 - a}{1^2} = - 2 \iff 2 - a = - 2 \iff a = 4$.
   Donc $f(x) = 2\ln x + \dfrac{4}{x} + b$. mais on sait que $f(1) = - 1$, soit $2\ln 1 + \dfrac{4}{1} + b = - 1 \iff b = - 1 - 4 = - 5$.
   Finalement : $f(x) = 2\ln x + \dfrac{4}{x} - 5$.

---

Partie B

---

Soit la fonction $f$ définie et dérivable sur $]0 ; +\infty[$ par $f(x) = 2\ln x + \dfrac{4}{x} - 5$.

1. 1. Déterminer $\displaystyle\lim_{x \to + \infty} f(x)$.
   On sait que $\displaystyle\lim_{x \to + \infty} \ln x = + \infty$ et que $\displaystyle\lim_{x \to + \infty} \dfrac{4}{x}$, d'où par somme de limites $\displaystyle\lim_{x \to + \infty} f(x) = + \infty$.
   2. On admet que $\displaystyle\lim_{x \to 0} f(x) = + \infty$. Que peut-on en déduire graphiquement ?
   $\displaystyle\lim_{x \to 0} f(x) = + \infty$ signifie que l'axe des ordonnées est asymptote verticale à $\mathcal{C}$ au voisinage de zéro.
2. 1. Pour tout nombre réel $x$ appartenant à $]0 ; +\infty[$, vérifier que $f'(x) = \dfrac{2x - 4}{x^2}$.
   On a $f'(x) = 2 \times \dfrac{1}{x} - \dfrac{4}{x^2} = \dfrac{2x - 4}{x^2}$.
   2. Étudier le signe de $f'(x)$ sur $]0 ; +\infty[$.
3. Établir le tableau de variations de $f$ sur $]0 ; +\infty[$.
Comme $x^2 > 0$ si $x \in ]0~;~ +\infty[$, le signe de $f'(x)$ est celui de $2x - 4$ qui est positif si $x > 2$.
Conclusion :
• $f'(x) > 0$ sur $]2~;~+ \infty[$ ;
• $f'(x) < 0 sur ]0~;~2[$ ;
• $f'(2) = 0$.

4. En précisant votre démarche, donner le nombre de solution(s) de l'équation $f(x) = 0$, pour $x$ appartenant à $]0 ; +\infty[$.
Comme $2\ln 2 - 3 \approx - 1,62$ est inférieur à zéro, la fonction décroissant de plus l'infini à $2\ln 2 - 3$ s'annule une fois sur l'intervalle ]0~;~2[, puis croissant de $2\ln 2 - 3$ à plus l'infini s'annule une autre fois sur l'intervalle $]2~;~+ \infty[$. L'équation $f(x) = 0$, pour $x$ appartenant à $]0~;~ +\infty[$ a donc deux solutions $\alpha$ et $\beta$.
5. 1. Donner le signe de $f(x)$ pour $x$ appartenant à $[1 ; 3]$.
   On a $f(1) = 2 \times 0 \dfrac{4}{1} - 5 = - 1$ et $f(3) = 2 \ln 3 + \dfrac{4}{3} - 5 = 2\ln 3 - \dfrac{11}{3} \approx - 1,47$.
   Donc sur l'intervalle $[1~;~3]$, $f$ ne prend que des valeurs négatives.
   2. On admet que la fonction $F$ définie pour $x$ appartenant à $]0 ; +\infty[$ par $F(x) = (2x + 4) \ln x - 7x$ est une primitive de $f$. Déterminer l'aire $\mathcal{A}$ du domaine limité par la courbe $\mathcal{C}$, l'axe des abscisses et les droites d'équation $x = 1$ et $x = 3$ en unités d'aires. On donnera la valeur exacte puis une valeur approchée à $10^{-2}$ près de $\mathcal{A}$.
   On a vu que sur l'intervalle [1~;~3], $f$ est négative, donc l'aire $\mathcal{A}$ du domaine limité par la courbe $\mathcal{C}$, l'axe des abscisses et les droites d'équation $x = 1$ et $x = 3$ est égale à $$\begin{array}{ll}\mathcal{A} = & \displaystyle\int_{1}^3 -f(x)\:\text{d}x \\ &= - \left[F(3) - F(1) \right] \\ &= F(1) - F(3) \\ &= (2\times 1 + 4) \ln 1 - 7\times 1 - \left[(2\times 3 + 4) \ln 3 - 7\times 3 \right] \\ &= - 7 - 10\ln 3 + 21 \\ &= 14 - 10\ln 3 ~\text{(unités d'aire).} \end{array}$$
   On a $\mathcal{A} = 14 - 10\ln 3 \approx 3,01$~unités d'aire.

 

Exercice 4 5 points

Probabilités

Une entreprise fabrique en grande quantité des médailles circulaires en argent. Un contrôle de qualité consiste à vérifier que le diamètre et l'épaisseur (exprimés en millimètres) sont conformes afin de les ranger dans un étui spécifique. Dans cet exercice, les valeurs approchées seront arrondies à $10^{-3}$ près.

---

Partie A

---

On suppose dans cette partie que la probabilité pour qu'une pièce prélevée au hasard soit conforme est égale à 0,9. Soit $X$ la variable aléatoire, qui à tout échantillon de 10 pièces associe le nombre de pièces conformes.

---

1. Justifier que la variable aléatoire $X$ suit une loi binomiale dont on déterminera les paramètres.
2. Calculer l'espérance mathématique $E(X)$ et l'écart type $\sigma(X)$ de la variable aléatoire $X$.
3. Calculer la probabilité que dans un échantillon de 10 pièces, au moins 8 pièces soient conformes.

---

Partie B

---

Les pièces sont fabriquées par une machine automatique. Soit $M$ la variable aléatoire qui à chaque pièce prélevée au hasard associe son diamètre. On suppose que $M$ suit la loi normale d'espérance 80 et d'écart type 0,6.

---

1. Déterminer la probabilité $P\left(79 \leqslant M \leqslant 81\right)$.
2. Quelle est la probabilité que le diamètre d'une pièce prélevée au hasard soit supérieur à 80 ?

---

Partie C

---

On s'intéresse dans cette partie à l'épaisseur des médailles. On fait l'hypothèse que le réglage de la machine est tel que 5$\,\% $des médailles fabriquées ont une épaisseur non conforme.

---

1. Déterminer l'intervalle de fluctuation asymptotique à 95$\,\% $de la fréquence des médailles non conformes obtenues dans un échantillon de 300 médailles.
2. On prélève un échantillon de 300 médailles. On constate que dans cet échantillon, 24 médailles ont une épaisseur non conforme. Doit-on réviser le réglage de la machine ?

Exercice 4 5 points

Probabilités

Une entreprise fabrique en grande quantité des médailles circulaires en argent. Un contrôle de qualité consiste à vérifier que le diamètre et l'épaisseur (exprimés en millimètres) sont conformes afin de les ranger dans un étui spécifique. Dans cet exercice, les valeurs approchées seront arrondies à $10^{-3}$ près.

---

Partie A

---

On suppose dans cette partie que la probabilité pour qu'une pièce prélevée au hasard soit conforme est égale à 0,9. Soit $X$ la variable aléatoire, qui à tout échantillon de 10 pièces associe le nombre de pièces conformes.

---

1. Justifier que la variable aléatoire $X$ suit une loi binomiale dont on déterminera les paramètres.

On répète $\1$  fois, de façon indépendante, l’expérience «\2 » qui comporte 2 issues :

• « \3 » considéré comme succès, de probabilité $p=\4$
• « \5 » considéré comme échec, de probabilité $q=1-p=\6$

Nous sommes donc en présence d’un schéma de Bernoulli et la variable aléatoire $\7$ prenant pour valeurs le nombre de succès obtenus suit la loi binomiale de paramètres $\1$  et $\4$ notée $\mathscr{B}(\1;\4)$ .

Pour tout entier $k$ où $0\leq k\leq \1$, on a $$P(\7=k)=\binom{\1}{k}\times \left(\4\right)^k\times\left( \6\right)^{\1-k}$$

2. Calculer l'espérance mathématique $E(X)$ et l'écart type $\sigma(X)$ de la variable aléatoire $X$.
On a E$(X) = n \times p = 10 \times 0,9 = 9$.
$\sigma(X) = \sqrt{n \times p\times (1 - p)} = \sqrt{10 \times 0,9 \times 0,1} = \sqrt{0,9}$.
3. Calculer la probabilité que dans un échantillon de 10 pièces, au moins 8 pièces soient conformes.
On veut $p(X \geqslant 8)= 1 - p( X\leq 7)$

 

2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$

$$P( \5 \leq \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
$p(X \geqslant 8) \approx \ 0,9298 \approx 0,93$

---

Partie B

---

Les pièces sont fabriquées par une machine automatique. Soit $M$ la variable aléatoire qui à chaque pièce prélevée au hasard associe son diamètre. On suppose que $M$ suit la loi normale d'espérance 80 et d'écart type 0,6.

---

1. Déterminer la probabilité $P\left(79 \leqslant M \leqslant 81\right)$.

2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$

$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$

 

2. Quelle est la probabilité que le diamètre d'une pièce prélevée au hasard soit supérieur à 80 ?
   • Méthode 1 : Comme l'espérance est égale à 80, la probabilité que le diamètre d'une pièce prélevée au hasard soit supérieur à $80$ est égale à $0,5$.
   • Méthode 2 :

      

     2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
     Avec une calculatrice de type TI

     $$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$

     $$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$

---

Partie C

---

On s'intéresse dans cette partie à l'épaisseur des médailles. On fait l'hypothèse que le réglage de la machine est tel que 5$\,\% $des médailles fabriquées ont une épaisseur non conforme.

---

1. Déterminer l'intervalle de fluctuation asymptotique à 95$\,\% $de la fréquence des médailles non conformes obtenues dans un échantillon de 300 médailles.

La proportion $p$ est égale à  $\1$. La taille  $n$  de l'échantillon considéré est égale à  $\2.$
Comme  $ n =\2$ ,   $n \times p  $=\3  et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.

En effet on a bien : $$n \geq 30\;;\; n \times p \geq 5 \text{ et } n\times (1-p) \geq 5$$


L'intervalle de fluctuation asymptotique au seuil de  $95\% $  est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$ 

$$I_{300} = [0,025~;~0,075]$$
2. On prélève un échantillon de 300 médailles. On constate que dans cet échantillon, 24 médailles ont une épaisseur non conforme. Doit-on réviser le réglage de la machine ?
Donc la fréquence d'apparition des médailles non conformes est : $f = \dfrac{24}{300} = \dfrac{8}{100} = 0,08$.
Or $0,8 \notin [0,025~;~0,075]$, donc au seuil de confiance de 95$\,\%$ on décide de revoir le réglage de la machine.