Rédigé par Luc Giraud le 20 juillet 2019. Publié dans Cours en TS.

Limites

Limites de fonctions

Limite au voisinage de $+\infty$

Limite finie en $+\infty$

Soit $l$ un réel. Dire que $f(x)$ a pour limite $l$ au voisinage de $+\infty$ signifie que tout intervalle ouvert contenant $l$ contient aussi toutes les valeurs de $f(x)$ pour x assez grand.

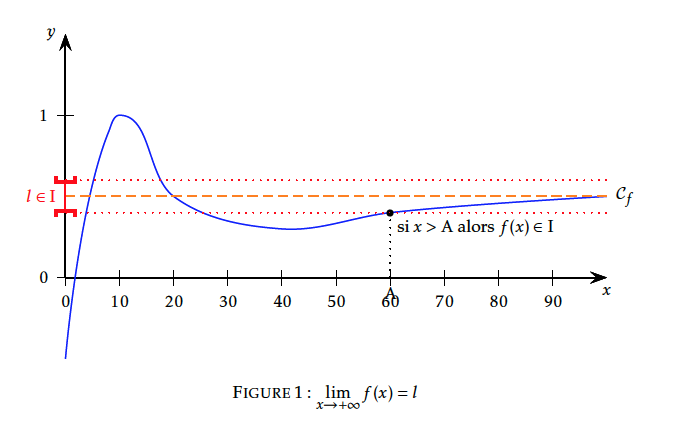
La droite d'équation $y=l$ est une asymptote horizontale à la courbe de $f$ au voisinage de $+\infty$.

Exemples :

$\lim\limits_{x\to+\infty}\dfrac{1}{x}=0$ et la droite d'équation $y=0$ est asymptote à la courbe de $f$ au voisinage de $+\infty$ (la droite est toujours en dessous de la courbe sur $[0;+\infty[$);
$\lim\limits_{x\to+\infty}\dfrac{-1}{x}=0$ et la droite d'équation $y=0$ est asymptote à la courbe de $f$ au voisinage de $+\infty$ (la droite est toujours au dessus de la courbe sur $[0;+\infty[$);
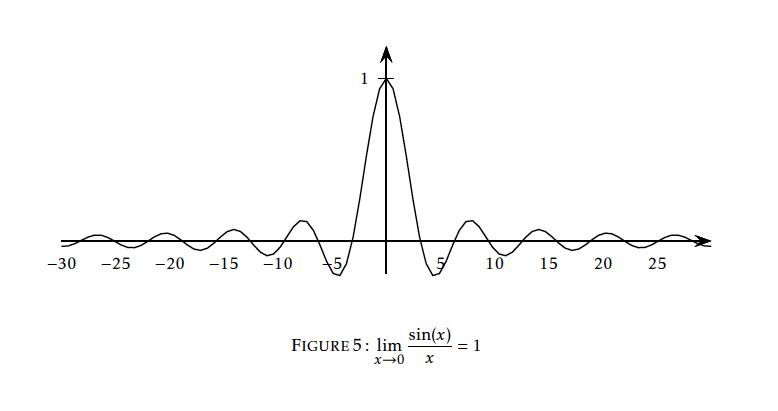
$\lim\limits_{x\to+\infty}\dfrac{\sin(x)}{x}=0$ et la droite d'équation $y=0$ est asymptote à la courbe de $f$ au voisinage de~$+\infty$ (la courbe coupe la droite en une infinité de points).

Limite infinie en $+\infty$

Dire que $f(x)$ a pour limite $+\infty$ (resp $-\infty$) au voisinage de $+\infty$ signifie que tout intervalle ouvert de la forme $]A;+\infty[$ (resp. $]-\infty;-A[$) contient aussi toutes les valeurs de $f(x)$ pour $x$ assez grand.

Soit $f$ une fonction définie sur un intervalle $I$ de la forme $]A;+\infty[$. S'il existe deux réels $a$ et $b$ tels que $f(x)=ax+b+g(x)$ avec $\lim\limits_{x\to+\infty}g(x)=0$ alors la droite $\Delta$ d'équation $y=ax+b$ est une asymptote oblique à la courbe de $f$ au voisinage de $+\infty$.

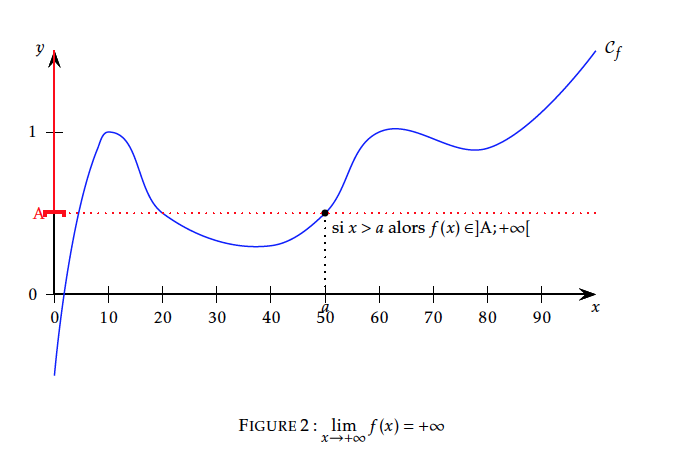
La courbe de $f:x\mapsto x+2+\dfrac{1}{x^2}$ admet une asymptote oblique d'équation $y=x+2$ au voisinage de $+\infty$ et au voisinage de $-\infty$.

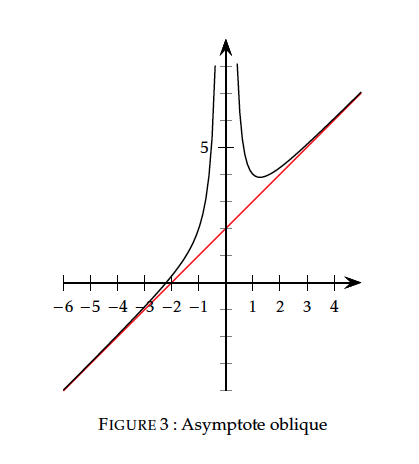
La limite en $\pm \infty$ d'un polynôme est égale à la limite en $\pm \infty$ de son monôme de plus haut degré.

La limite d'une fonction rationnelle (quotient de deux polynômes) en $\pm \infty$ est égale à la limite en $\pm \infty$ du quotient des monômes de plus haut degré du numérateur et du dénominateur.

Limite au voisinage d'un réel $a$

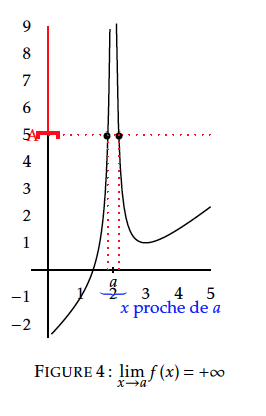
[Limite infinie en $a$] Dire que $f(x)$ a pour limite $+\infty$ (resp. $-\infty$) au voisinage de $a$ signifie que tout intervalle ouvert de la forme $]A;+\infty[$ (resp. $]-\infty;-A[$) contient aussi toutes les valeurs de $f(x)$ pour $x$ assez proche de $a$.

La droite d'équation $x=a$ est une asymptote verticale à la courbe de $f$.

[Limite finie en $a$] Soit $l$ un réel. Dire que $f(x)$ a pour limite $l$ au voisinage de $a$ signifie que tout intervalle ouvert contenant $l$ contient aussi toutes les valeurs de $f(x)$ pour $x$ assez proche de $a$.

Soit $f$ la fonction définie sur $\mathbb{R}^*$ par $f(x)=\dfrac{\sin(x)}{x}$. On a
$$\begin{array}{ll} \lim\limits_{x\to0}f(x)&=\lim_{x\to0}\dfrac{\sin(x)-0}{x-0} \\ &= \lim\limits_{x\to0}\dfrac{\sin(x)-\sin(0)}{x-0}\\ &=\cos(0) \quad\text{ par définition du nombre dérivé }\\ &=1\\\end{array}$$

Donc$$\lim_{x\to 0}\dfrac{\sin(x)}{x}=1$$

Opérations sur les limites

Dans les théorèmes admis ci-dessous, présentés sous forme de tableaux,$u$ et $v$ sont des fonctions définies sur un même intervalle $I$ et $\bigcirc$ désigne $+\infty ,-\infty$ ou un nombre réel $a$; $L$ et $L'$ sont des nombres réels.

somme

Comment déterminer $\displaystyle\lim_{x \to \bigcirc}[u(x)+v(x)]$? $$\begin{array}{ |c|c|c|c|c|c|c| } \hline \text{ Si } \displaystyle\lim_{x \to \bigcirc}u(x)& L\in \mathbb{R} & L & L & +\infty & +\infty & -\infty \\ \hline \text{ et } \displaystyle\lim_{x \to \bigcirc} v(x) & L'\in \mathbb{R} & +\infty & -\infty & +\infty & -\infty & -\infty \\ \hline \text{ alors }\displaystyle\lim_{x \to \bigcirc}[u(x)+v(x)] & L+L' & +\infty & -\infty & +\infty & ? & -\infty \\ \hline \end{array} $$ Les points d'interrogation ( ?) signalent les cas indéterminés. Ce sont des cas pour lesquels une étude spécifique doit être menée pour déterminer une éventuelle limite.

Cas du produit d'une fonction par une constante

On suppose que la constante $k$ n'est pas nulle. Comment déterminer $\displaystyle\lim_{x \to \bigcirc}[ku(x) ]$?

$$\begin{array}{ |c|c|c|c|c|c| } \hline \text{ Si }\displaystyle\lim_{x \to \bigcirc}u(x) & L\in \mathbb{R} & +\infty & +\infty & -\infty & -\infty \\ \hline \text{ alors } \displaystyle\lim_{x \to \bigcirc} [ku(x)] & kL & +\infty \text{ si } k>0 & -\infty \text{ si } k < 0 & -\infty \text{ si } k > 0 & +\infty \text{ si } k < 0 \\ \hline \end{array} $$

Cas du produit de deux fonctions

Comment déterminer $\displaystyle\lim_{x \to \bigcirc}[u(x)\times v(x) ]$? $$\begin{array}{ |c|c|c|c|c|c| } \hline \text{ Si } \displaystyle\lim_{x \to \bigcirc}u(x)& L\in \mathbb{R} & L\neq 0 & 0 & +\infty \text{ ou } -\infty \\ \hline et \displaystyle\lim_{x \to \bigcirc} v(x) & L' & +\infty \text{ ou } -\infty& +\infty \text{ ou } -\infty& +\infty \text{ ou } -\infty \\ \hline alors \displaystyle\lim_{x \to \bigcirc} [u(x)\times v(x)] & LL' & \pm\infty & \textbf{?} & \pm\infty \\ \hline \end{array}$$ $ \pm \infty$ correspond soit à $+\infty$, soit à $-\infty$. Le signe + ou - s'obtient de façon évidente dans chaque exemple.

Cas de l'inverse :

Comment déterminer $\displaystyle\lim_{x \to \bigcirc} \dfrac{1}{u(x)} $?
$$ \begin{array}{ |c|c|c|c|c| } \hline \text { Si } \displaystyle\lim_{x \to \bigcirc}u(x)& L\neq 0 & 0 & +\infty \text{ ou } -\infty \\ \hline alors \displaystyle\lim_{x \to \bigcirc} \dfrac{1}{u(x)} & \dfrac{1}{L} &\text{ voir le théorème ci dessous } & 0 \\ \hline \end{array} $$

Si $\displaystyle\lim_{x \to \bigcirc}u(x)=0$ et si au voisinage de $\bigcirc$ on a $u(x)>0$, alors on a $\displaystyle\lim_{x \to \bigcirc} \dfrac{1}{u(x)} =+\infty$
Si $\displaystyle\lim_{x \to \bigcirc}u(x)=0$ et si au voisinage de $\bigcirc$ on a $u(x)<0$, alors on a $\displaystyle\lim_{x \to \bigcirc} \dfrac{1}{u(x)} =-\infty$

Cas du quotient :

Sur tout intervalle où le quotient $\dfrac{u(x)}{v(x)}$ est défini, on remarque que $\dfrac{u(x)}{v(x)}=u(x)\times \dfrac{1}{v(x)}$ et on utilise les théorèmes de l'inverse $\dfrac{1}{v(x)}$ et la limite d'un produit.

Limite d'une fonction composée

Soit $g$ et $h$ deux fonctions telles que: $$x\stackrel{g}{ \mapsto}y\stackrel{h}{ \mapsto}z=h(y)=h(g(x))=h \circ g(x)$$ Si $\displaystyle\lim_{x \to a}g(x)=b$ et si $\displaystyle\lim_{y \to b}h(y)=c$, alors $\displaystyle\lim_{x \to a}h(g(x))=c$

Un exemple ?
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=\sqrt{3x^2+5}$. Cherchons $\displaystyle\lim_{x \to-\infty}f(x)$.

On a $\displaystyle\lim_{x \to-\infty}3x^2+5=+\infty$ et $\displaystyle\lim_{y \to +\infty}\sqrt{y}=+\infty$ donc par composée: $\displaystyle\lim_{x\to-\infty}\sqrt{3x^2+5}=+\infty$

Limites et ordre

Compatibilité avec l'ordre : Soit $a$ un réel, $+\infty$ ou $-\infty$. Soit $f$ et $g$ deux fonctions telles que $\lim\limits_{x \to a}f(x)=l$ et $\lim\limits_{x \to a}g(x)=l'$.
Si $f(x)< g(x)$ alors $l \leq l'$

Théorème des gendarmes: Soit trois fonctions $f$, $g$ et $h$ telles que $f(x)\leq g(x) \leq h(x)$ au voisinage de $a$ (réel ou $\pm\infty$). Si les fonctions $f$ et $h$ ont la m\^eme \emph{limite finie} $l$ au voisinage de $a$, alors $g$ a pour limite $l$ au voisinage de $a$.

À connaître On démontre ce théorème dans le cas particulier de $+\infty$ .
Soit $I$ un intervalle ouvert contenant $l$, on doit montrer que $I$ contient tous les réels $g(x)$ pour $x$ assez grand. Par hypothèse,

$\lim\limits_{x \to +\infty}f(x)=l$ donc $I$ contient tous les réels $f(x)$ pour $x$ assez grand, plus précisément, il existe un réel $A$ tel que si $x>A$ alors $f(x)\in I$.
$\lim\limits_{x \to +\infty}h(x)=l$ donc $I$ contient tous les réels $h(x)$ pour $x$ assez grand, plus précisément, il existe un réel $B$ tel que si $x>B$ alors $h(x)\in I$.

Posons $N=\text{max}(A;B)$ alors pour $x>N$, on a $f(x)\in I$ et $h(x)\in I$.\par Dire que $f(x)\leq g(x) \leq h(x)$ au voisinage de $+\infty$, signifie qu'il existe un réel $C$ tel que pour $x>C$, on a $f(x)\leq g(x) \leq h(x)$.

Posons $M=\text{max}(N;C)$ alors pour $x>M$, on a $f(x)\in I$, $h(x)\in I$ et $f(x)\leq g(x) \leq h(x)$.

On en déduit que pour $x>M$, on a $g(x)\in I$; c'est-à-dire que $I$ contient les réels $g(x)$ pour $x$ assez grand.

Soit $f$ la fonction définie sur $\mathbb{R}^*$ par $f(x)=x\sin\left(\dfrac{1}{x}\right)$.\par Pour tout $x>0$, on a $-x\leq f(x) \leq x$

Comme $\displaystyle{\lim_{x \to 0^+}x= \lim_{x \to 0^+}(-x)=0}$, on en déduit que $\displaystyle\lim_{x \to 0^+}f(x)=0$.

De même pour $x<0$, on obtient $\displaystyle\lim_{x \to 0^-}f(x)=0$.

Donc $\displaystyle\lim_{x \to 0}f(x)=0$.

Corollaire du théorème des gendarmes
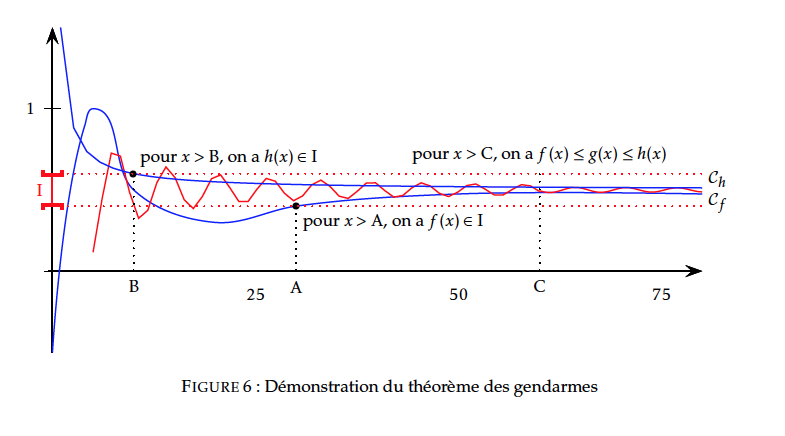
Soit deux fonctions $f$ et $g$ telles que $f\leq g $ au voisinage de $a$ (réel ou $\pm\infty$),

si $\lim\limits_{x\to a}f(x)=+\infty$ alors $\lim\limits_{x\to a}g(x)=+\infty$;
si $\lim\limits_{x\to a}g(x)=-\infty$ alors $\lim\limits_{x\to a}f(x)=-\infty$.

EXERCICES

Avec les définitions

Exercice
On considère la fonction $f$ définie sur $]0,+\infty[$ par $f(x)=\dfrac{2x^2+1}{x^2}$

Donner des valeurs approchées à $10^{-3}$ près de $f(1)$, $f(32)$, $f(320)$ et $f(3232)$.
Observer la représentation graphique de $f$ donnée par une calculatrice ou un ordinateur. Quelle conjecture peut-on faire sur la limite de $f$ en $+\infty$ ?
On considère l'intervalle ouvert de centre 2 et de rayon 0,01 , c'est-à -dire $]1,99 ; 2,01[$ . Démontrer que pour $x > 10$ , $f(x)\in ]1,99 ; 2,01[$ (On pourra écrire $f(x)$ sous la forme $f(x)=2+1/x^2$ )
On considère l'intervalle $]2-r, 2+r[$ avec $r>0$. Montrer que pour $x$ supérieur à un certain $x_0$ à déterminer en fonction de $r$ , tous les $f(x)$ appartiennent à l'intervalle $]2-r,2+r[$.
Démontrer que $\lim\limits_{x\to+\infty} f(x)=2$

Exercice

On considère la fonction $g$ définie sur $\mathbb{R}$ par $3x^3+x^2$

Donner les valeurs de $g(32)$, $g(320)$ et $g(3232)$.
Observer la représentation graphique de $g$ donnée par une calculatrice ou un ordinateur. Quelle conjecture peut-on faire sur la limite de $g$ en $+\infty$ ?
On considère l'intervalle $]100; +\infty[$ . Démontrer que pour $x > 10$, $f(x)\in\ ]100,+\infty[$.
On considère un intervalle $]A,+\infty[$ , avec A > 0. Montrer que pour $x$ supérieur à $\sqrt{A}$ , tous les $f(x)$ appartiennent à l'intervalle $]A ; +\infty[$ .

Exercice

Soit $h$ définie sur $\mathbb{R}$ par $h(x)=-2x+3$ Démontrez que $\lim\limits_{x\to+\infty}f(x)=-\infty$

Exercice

On considère la fonction $h$ définie sur $]1,+\infty[$ par $h(x)=2+\dfrac{3}{(x-1)^2}$

Justifiez que $h$ est bien définie sur $]1,+\infty[$.
Observer la représentation graphique de $h$ donnée par une calculatrice ou un ordinateur. Quelle conjecture peut-on faire sur la limite de $h$ en $1$ ?
On considère l'intervalle $]1000; +\infty[$ . Donnez une condition suffisante portant sur $x$ pour que $h(x)\in\ ]1000,+\infty[$.
On considère un intervalle $]A,+\infty[$ , avec A > 2. Donnez une condition suffisante portant sur $x$ pour que $h(x)\in ]A ; +\infty[$ .
Justifiez que $\lim\limits_{x\to 1} h(x)=+\infty$.

Avec les théorèmes

Exercice

Limite en zéro Soit $f~:~x\mapsto \dfrac{|x|}{x}$. Étudiez sa limite en zéro.

Exercice

De la géométrie pour calculer une limite
Voici une première méthode de calcul de $\lim\limits_{x \to 0}\dfrac{\sin x}{x}$. Pourquoi suffit-il d'étudier la limite pour des valeurs de $x>0$ ? Utilisez une figure pour obtenir que, pour tout $x\in]0,\pi/2[$,

$$\sin x< x <\tan x$$ Déduisez-en un encadrement de $\dfrac{\sin x}{x}$ pour tout $x\in]0,\pi/2[$ et concluez après avoir étudié la parité de la fonction.

Exercices : Limites trigonométriques

En supposant connu le résultat de l'exercice précédent, calculez $\lim\limits_{x \to 0}\dfrac{\tan x}{x}$ et $\lim\limits_{x \to 0}\dfrac{1-\cos x}{x^2}$

Pour la 2éme, utilisez la formule bien connue $\cos(2a)=1-2\sin^2(a)$

Exercice : Limite et radicaux

Calculez :

$ \lim\limits_{x\to 0}\dfrac{\sqrt{1+x}-1}{x}$
$ \lim\limits_{x\to +\infty}{\sqrt{x^2+1}-x} $
$ \lim\limits_{x\to 0}\dfrac{x^2}{1-\sqrt{1-x^2}}$

Calculs stakhanovistes

Applications directes du cours

Exercice

Étudier les limites des fonctions suivantes au voisinage de $+\infty$:

$x^2-5x+6$;
$-4x^2+6x-7$;
$\dfrac{2x+1}{x-1}$;
$\dfrac{2x^2-3x+5}{x^3+x-3}$;
$\dfrac{x^3}{x^2+1}-x$;
$\dfrac{2x-\sqrt{x}}{\sqrt{x}-3}$.

Exercice

Étudier les limites des fonctions suivantes au voisinage de $+\infty$:

$\dfrac{x+\sin(x)}{-2x+\cos(x)}$;
$2x-\sqrt{x^2+3x-1}$;
$\dfrac{\sqrt{x^2-2x+3}}{x}$.

Étudier les limites des fonctions suivantes au voisinage de $a$:

$\dfrac{x+4}{x^2+3x+2}$ en $a=-2$;
$\dfrac{x+2}{x^2+3x+2}$ en $a=-2$;
$\dfrac{-x^2+x+6}{2x^2-5x+2}$ en $a=2$;
$\dfrac{\sqrt{x+1}}{x}$ en $a=0$;
$\dfrac{\sqrt{x+1}-1}{x}$ en $a=0$;
$\dfrac{\sqrt{x+4}-2}{x}$ en $a=0$;
$\tan(x)$ en $a=\dfrac{\pi}{2}$;
$\dfrac{\sin(3x)}{x}$ en $a=0$.

Exercice

Soit $f$ la fonction définie par : \[f(x)=\dfrac{-x^3+2x^2-x+3}{x^2+1} \,.\]

Déterminer trois réels $a$, $b$ et $c$ tels que $f(x)=ax+b+\dfrac{c}{x^2+1}$.
Calculer la limite de $f(x)-(ax+b)$ en $+\infty$ puis en $-\infty$.
En déduire que la courbe représentative de $f$, $\mathcal{C}$ admet une asymptote oblique $\Delta$ en $-\infty$ et en $+\infty$.
Étudier les positions relatives de $\mathcal{C}$ et de $\Delta$.

Approfondissement

Exercice

Étudier les limites des fonctions suivantes :

$\sqrt{x^2+1}-\sqrt{x^2-1}$ en $+\infty$;
$x\left(\sqrt{\dfrac{x+1}{x-1}}-1\right)$ en $+\infty$;
$\dfrac{\sqrt{x^2+1}-\sqrt{x+3}}{x^2-2x}$ en $2$;
$\dfrac{\tan(x)}{x}$ en $0$;
$\dfrac{\sin(ax)}{\sin(bx)}$ en $0$ avec $ab\neq0$;
$x\sin\left(\dfrac{1}{x}\right)$ en $+\infty$.

Exercice

Étudier selon les valeurs de $a$ et de $b$ les limites de

$f:x\mapsto\sqrt{x^2+5x+1}+ax+b$ en $+\infty$ et en $-\infty$
$g:x\mapsto\dfrac{ax^2-(2a+1)x+2}{x-1}$ en 1.

Exercice

Question de cours (Métropole, Nouvelle Calédonie novembre 2007)

Soit $f$ une fonction réelle définie sur $[a~;~+ \infty[$. Compléter la phrase suivante : « On dit que $f$ admet une limite finie $\ell$ en $+ \infty$ si ... »
Démontrer le théorème « des gendarmes » : soient $f,~g$ et $h$ trois fonctions définies sur $[a~;~+ \infty[$ et $\ell$ un nombre réel. Si $g$ et $h$ ont pour limite commune $\ell$ quand $x$ tend vers $+ \infty$, et si pour tout $x$ assez grand $g(x) \leqslant f(x) \leqslant h(x)$, alors la limite de $f$ quand $x$ tend vers $+ \infty$ est égale à $\ell$.

Recettes à Bac

Comment étudier la position relative de deux courbes ?

Soit $C_f$ la courbe d'équation $y=f(x)$ et $C_g'$ la courbe d'équation $y=g(x)$. Pour étudier la position relative de $C_f$ et $C_g$, il faut étudier le signe de $f(x)-g(x)$. En effet, si nous obtenons par exemple $f(x)-g(x)\geq 0$ sur l'intervalle $I$, alors $f(x)\geq g(x)$ sur $I$ et donc $C_f$ est au-dessus de $C_g$ sur $I$.

Comment montrer qu'une courbe admet une asymptote d'équation $y=ax+b$ au voisinage de $\omega$ ?

Il suffit de montrer que $\left[f(x)-(ax+b)\right]$ tend vers 0 quand $x$ tend vers $\omega$.

Asymptote horizontale

Si une fonction $f$ vérifie \[\lim_{x\to+\infty}f(x)=\ell\] alors la droite d'équation $y=\ell$ est une asymptote horizontale en $+\infty$ à la courbe représentative de $f$.

\[\lim_{x\to +\infty}f(x)=2 \,.\] Soit $f$ la fonction définie par \[f(x) = \dfrac{x^{2} - x +1}{x^{3} + 1}\,.\] Montrer que $\lim\limits_{x\to+\infty}f(x) = 0$. Interpréter graphiquement ce résultat.

Asymptote verticale

Soit $a$ un réel. Si une fonction $f$ vérifie \[\lim_{x\to a}f(x)= + \infty \] alors la droite d'équation $x=a$ est une asymptote verticale à la courbe représentative de~$f$.

\[\lim_{x\to 2 \atop x>2}f(x)= + \infty \text{ et } \lim_{x\to 2 \atop x<2}f(x)= - \infty \,.\] Soit $f$ la fonction définie par \[f(x) = \dfrac{x^{2} - x +1}{x - 1}\,.\] Étudier les limites de $f$ au voisinage de 1 puis interpréter graphiquement ce résultat.

Asymptote oblique

Soit $\Delta$ la droite d'équation $y=mx+p$. Si une fonction $f$ vérifie \[\lim_{x\to +\infty}\left(f(x)-(mx+p)\right)= 0 \] alors la droite d'équation $\Delta$ est une asymptote oblique au voisinage de $+\infty$ à la courbe représentative de~$f$.

\[\lim_{x\to -\infty}\left(f(x)-(mx+p)\right)=0 \text{ et } \lim_{x\to +\infty}\left(f(x)-(mx+p)\right)= 0\,.\] Soit $f$ la fonction définie sur $]0;+\infty[$ par \[f(x) = \dfrac{\sqrt{x+1}}{x^2} + 2x -1\,.\] Prouver que la droite $\Delta$ d'équation $y=2x-1$ est une asymptote oblique à la courbe représentative de $f$ au voisinage de $+\infty$.

Comment montrer qu'une fonction est paire ?

Il faut vérifier que l'ensemble de définition de $f$ est symétrique par rapport à zéro puis que pour tout réel $x$ de l'ensemble de définition $f(-x)=f(x)$. Nous en déduisons que la courbe est symétrique par rapport à l'axe des ordonnées. Il suffira donc d'étudier la fonction sur la << moitié >> de l'ensemble de définition, puis de déduire le reste de la courbe par symétrie.

Comment montrer qu'une fonction est impaire ?

cf le paragraphe précédent en remplaçant $f(-x)=f(x)$ par $f(-x)=-f(x)$ et <<~symétrique par rapport à l'axe des ordonnées~>> par << symétrique par rapport à l'origine du repère >>.

Comment montrer qu'une courbe admet le point $A(a,b)$ comme centre de symétrie~?

Faites avant tout un dessin pour visualiser que $A$ est le milieu du segment $[MM']$ avec $M (x,f(x) )$ et $M' (x',f(x') )$. Alors d'une part $\dfrac{x+x'}{2}=a$, donc $x'=2a-x$ et d'autre part $\dfrac{f(x)+f(x')}{2}=b$, $i.e.$ $$f(x)+f(2a-x)=2b$$

Comment montrer qu'une fonction est périodique ?

Il s'agit de trouver un réel $T$ tel que pour tout réel $x$ appartenant à l'ensemble de définition de $f$, alors $$f(x+T)=f(x)$$ Il suffira alors d'étudier la fonction sur un intervalle de longueur $T$, par exemple $[0,T]$, puis de déduire le reste de la courbe par des translations successives de vecteur $k\vec{i}$, avec $k\in \mathbb{Z}$. Vous connaissez bien sûr la fonction sinus qui vérifie $\sin(x+2\pi)=\sin x$ pour tout réel $x$ et qui est donc $2\pi$-périodique.

Comment étudier le signe d'une expression ?

Vaste problème...Retenir malgré tout qu'en règle général, nous savons étudier le signe d'un produit ou d'un quotient de polynômes du 1^er ou du 2^nd degré, d'exponentielles ( qui sont toujours positives ), de cosinus ou de sinus, de logarithmes népériens...

Vous chercherez donc en général à factoriser ou à réduire au même dénominateur votre expression. Si cela s'avère impossible algébriquement, on vous suggérera d'étudier une fonction. Alors soit elle admettra comme extremum zéro, soit vous déterminerez une approximation de la valeur d'annulation de $f$ grâce au théorème de la bijection et vous conclurez à l'aide du tableau de variations.

Qu'est-ce qu'une fonction croissante sur $I$ ?

C'est une fonction qui conserve l'ordre sur $I$.

Comment lever une indétermination ?

Il n'y a pas une méthode mais des méthodes. Il ne s'agit donc pas d'apprendre par c\oe ur des recettes (tiens tiens...), ce qui vous induirait à écrire de grosses sottises. Vous pouvez dans un premier temps repérer des termes <<~négligeables~>> devant d'autres et factoriser par le plus <<~fort~>> (c'est le cas par exemple des fonctions rationnelles au voisinage de $+\infty$ ou $-\infty$). Vous pouvez minorer ou majorer par des valeurs permettant de conclure à l'aide des théorèmes de comparaison (c'est le cas de la fonction cosinus qui vérifie \[-1\leq\cos x\leq 1\] pour tout réel $x$ et donc \[-\dfrac{1}{x}\leq \dfrac{\cos x}{x}\leq \dfrac{1}{x}\] pour $x\geq 0$ et finalement \[\displaystyle\lim_{x\to+\infty}\dfrac{\cos x}{x}=0\] par application du théorème des gendarmes. Vous pouvez utiliser les propriétés algébriques de certaines fonctions pour retrouver des limites connues ( $x^2+1=\sqrt{x^2+1}\sqrt{x^2+1}$...) Dans le cas de l'étude de limites de fonctions irrationnelles, le recours à la quantité conjuguée peut s'avérer utile. Dans les cas désespérés, vous pouvez essayer de reconnaàître la limite d'un taux de variation et donc utiliser la dérivée associée.

Vues: 9280

Imprimer