Limites - page 2
Page 2 sur 5
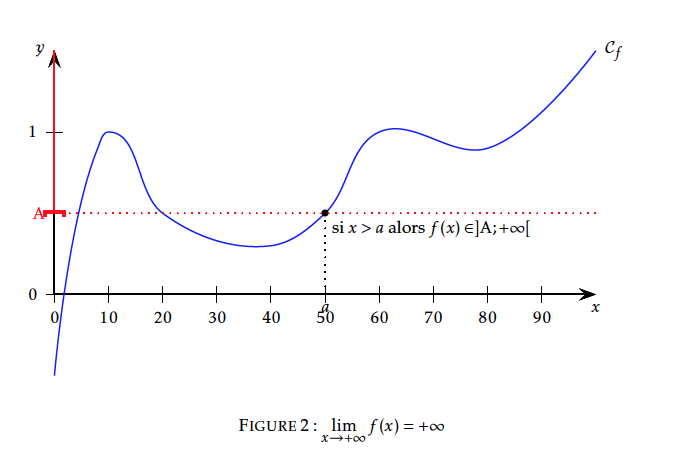
Limite infinie en $+\infty$
Dire que $f(x)$ a pour limite $+\infty$ (resp $-\infty$) au voisinage de $+\infty$ signifie que tout intervalle ouvert de la forme $]A;+\infty[$ (resp. $]-\infty;-A[$) contient aussi toutes les valeurs de $f(x)$ pour $x$ assez grand.
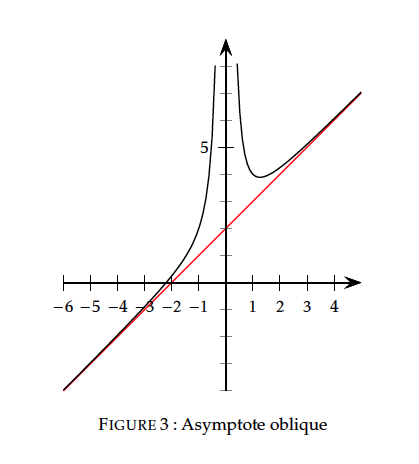
Soit $f$ une fonction définie sur un intervalle $I$ de la forme $]A;+\infty[$. S'il existe deux réels $a$ et $b$ tels que $f(x)=ax+b+g(x)$ avec $\lim\limits_{x\to+\infty}g(x)=0$ alors la droite $\Delta$ d'équation $y=ax+b$ est une asymptote oblique à la courbe de $f$ au voisinage de $+\infty$.
La courbe de $f:x\mapsto x+2+\dfrac{1}{x^2}$ admet une asymptote oblique d'équation $y=x+2$ au voisinage de $+\infty$ et au voisinage de $-\infty$.
La limite en $\pm \infty$ d'un polynôme est égale à la limite en $\pm \infty$ de son monôme de plus haut degré.
La limite d'une fonction rationnelle (quotient de deux polynômes) en $\pm \infty$ est égale à la limite en $\pm \infty$ du quotient des monômes de plus haut degré du numérateur et du dénominateur.
Limite au voisinage d'un réel $a$
[Limite infinie en $a$] Dire que $f(x)$ a pour limite $+\infty$ (resp. $-\infty$) au voisinage de $a$ signifie que tout intervalle ouvert de la forme $]A;+\infty[$ (resp. $]-\infty;-A[$) contient aussi toutes les valeurs de $f(x)$ pour $x$ assez proche de $a$.
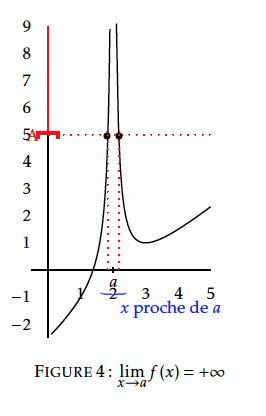
La droite d'équation $x=a$ est une asymptote verticale à la courbe de $f$.
[Limite finie en $a$] Soit $l$ un réel. Dire que $f(x)$ a pour limite $l$ au voisinage de $a$ signifie que tout intervalle ouvert contenant $l$ contient aussi toutes les valeurs de $f(x)$ pour $x$ assez proche de $a$.
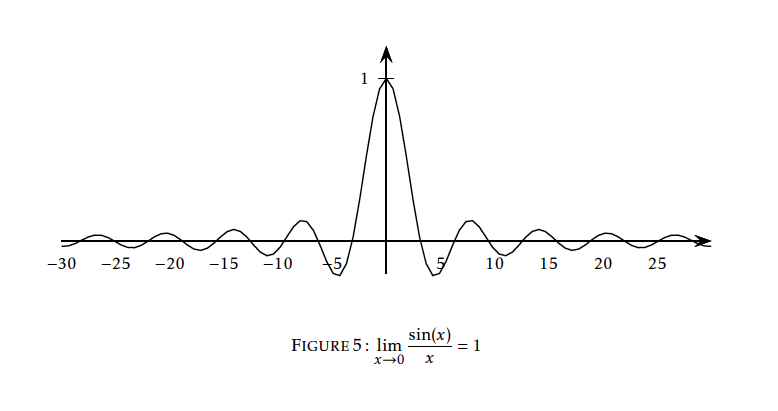
Soit $f$ la fonction définie sur $\mathbb{R}^*$ par $f(x)=\dfrac{\sin(x)}{x}$. On a
$$\begin{array}{ll} \lim\limits_{x\to0}f(x)&=\lim_{x\to0}\dfrac{\sin(x)-0}{x-0} \\ &= \lim\limits_{x\to0}\dfrac{\sin(x)-\sin(0)}{x-0}\\ &=\cos(0) \quad\text{ par définition du nombre dérivé }\\ &=1\\\end{array}$$
Donc$$\lim_{x\to 0}\dfrac{\sin(x)}{x}=1$$
Limites et opérations
Page
- 1
- 2
- 3
- 4
- 5
- Toutes les pages
- Vues: 9306
