Baccalauréat S Polynésie 19 juin 2019 - Exercice 4
Page 7 sur 10
Exercice 4 5 points
Sur la figure donnée en annexe 2 à rendre avec la copie :
- ABCDEFGH est un parallélépipède rectangle tel que AB $= 12$, AD $= 18$ et AE $= 6$
- EBDG est un tétraèdre.
L'espace est rapporté à un repère orthonormal d'origine A dans lequel les points B, D et E ont pour coordonnées respectives B(12 ; 0 ; 0), D(0 ; 18 ; 0) et E(0 ; 0 ; 6).
- Démontrer que le plan (EBD) a pour équation cartésienne $3x + 2y + 6z - 36 = 0$.
-
- Déterminer une représentation paramétrique de la droite (AG).
- En déduire que la droite (AG) coupe le plan (EBD) en un point K de coordonnées (4 ; 6 ; 2) .
- La droite (AG) est-elle orthogonale au plan (EBD) ? Justifier.
-
- Soit M le milieu du segment [ED]. Démontrer que les points B, K et M sont alignés.
- Construire alors le point K sur la figure donnée en annexe 2 à rendre avec la copie.
- On note P le plan parallèle au plan (ADE) passant par le point K.
- Démontrer que le plan P coupe le plan (EBD) selon une parallèle à la droite (ED).
- Construire alors sur l'annexe 2 à rendre avec la copie l'intersection du plan P et de la face EBD du tétraèdre EBDG.
ANNEXE 2
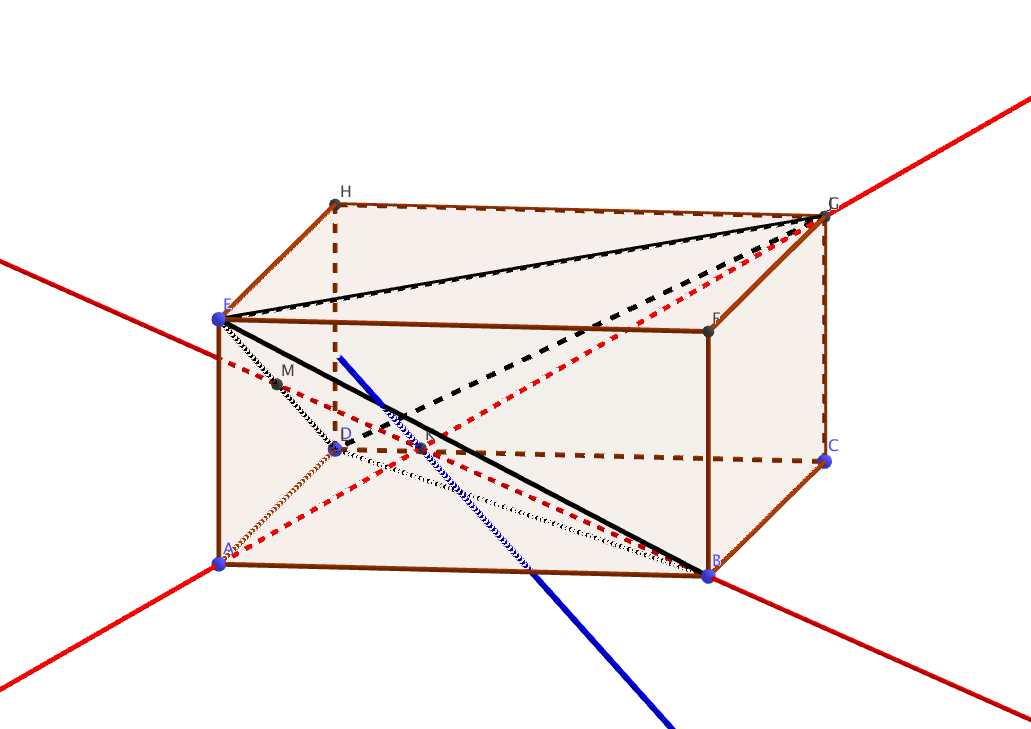
- Vues: 48685
