Baccalauréat S Centres étrangers 13 juin 2019
Exercice 1 4 points
Cet exercice est un questionnaire à choix multiples (Q. C. M.) qui envisage quatre situations relatives à une station de ski.
Les quatre questions sont indépendantes.
Pour chacune des questions, une seule des quatre réponses est exacte. Le candidat indiquera sur sa copie le numéro de la question et la lettre correspondant à la réponse exacte. Aucune justification n'est demandée . Une réponse exacte rapporte un point, une réponse fausse ou une absence de réponse ne rapporte ni n'enlève aucun point.
- Une étude statistique a établi qu'un client sur quatre pratique le surf. Dans une télécabine accueillant 80 clients de la ,station, la probabilité arrondie au millième qu'il y ait exactement 20 clients pratiquant le surf est :
- 0,560
- 0,25
- 1
- 0,103
- L'épaisseur maximale d'une avalanche, exprimée en centimètre, peut être modélisée par une variable aléatoire X qui suit une loi normale de moyenne μ=150 cm et d'écart-type inconnu. On sait que P(X⩾200)=0,025. Quelle est la probabilité P(X⩾100) ?
- On ne peut pas répondre car il manque des éléments dans l'énoncé.
- 0,025
- 0,95
- 0,975
- Dans un couloir neigeux, on modélise l'intervalle de temps séparant deux avalanches successives, appelé temps d'occurrence d'une avalanche, exprimé en année, par une variable aléatoire T qui suit une loi exponentielle. On a établi qu'une avalanche se déclenche en moyenne tous les 5~ans. Ainsi E(T)=5. La probabilité P(T⩾5) est égale à :
- 0,5
- 1−e−1
- e−1
- e−25
- L'office de tourisme souhaite effectuer un sondage pour estimer la proportion de clients satisfaits des prestations offertes dans la station de ski. Pour cela, il utilise un intervalle de confiance de longueur 0,04 avec un niveau de confiance de 0,95. Le nombre de clients à interroger est :
- 50
- 2500
- 25
- 625
Correction de l'exercice 1 (4 points)
Cet exercice est un questionnaire à choix multiples (Q. C. M.) qui envisage quatre situations relatives à une station de ski.
Les quatre questions sont indépendantes.
Pour chacune des questions, une seule des quatre réponses est exacte. Le candidat indiquera sur sa copie le numéro de la question et la lettre correspondant à la réponse exacte. Aucune justification n'est demandée . Une réponse exacte rapporte un point, une réponse fausse ou une absence de réponse ne rapporte ni n'enlève aucun point.
- Une étude statistique a établi qu'un client sur quatre pratique le surf. Dans une télécabine accueillant 80 clients de la ,station, la probabilité arrondie au millième qu'il y ait exactement 20 clients pratiquant le surf est :
- 0,560
- 0,25
- 1
- 0,103
On appelle X la variable aléatoire comptant le nombre de clients pratiquant le surf.
- On effectue 80 tirages aléatoires, indépendants, identiques. À chaque tirage il y a deux issues :
- – S : “le client pratique le surf”;
- – ¯S : “le client ne pratique pas le surf”.
- De plus p(S)=0,25
- La variable aléatoire X suit donc la loi binomiale de paramètres n=80 et p=0,25.
- Par conséquent :
- P(X=20)=(8020)×0,2520×0,7560≈0,103
Réponse d
- L'épaisseur maximale d'une avalanche, exprimée en centimètre, peut être modélisée par une variable aléatoire X qui suit une loi normale de moyenne μ=150 cm et d'écart-type inconnu. On sait que P(X⩾200)=0,025. Quelle est la probabilité P(X⩾100) ?
- On ne peut pas répondre car il manque des éléments dans l'énoncé.
- 0,025
- 0,95
- 0,975
On a P(X≥200)=P(X≥150+50)=0,025
- Donc P(X≤150−50)=0,025 soit P(X≤100)=0,025.
- Ainsi P(X≥100)=1−0,025=0,975.
Réponse d
- Dans un couloir neigeux, on modélise l'intervalle de temps séparant deux avalanches successives, appelé temps d'occurrence d'une avalanche, exprimé en année, par une variable aléatoire T qui suit une loi exponentielle. On a établi qu'une avalanche se déclenche en moyenne tous les 5~ans. Ainsi E(T)=5. La probabilité P(T⩾5) est égale à :
- 0,5
- 1−e−1
- e−1
- e−25
E(T)=5 par conséquent la variable aléatoire suit la loi exponentielle de paramètre λ=15=0,2.
- Ainsi P(T≥5)=e−0,2×5=e−1
Réponse c
- L'office de tourisme souhaite effectuer un sondage pour estimer la proportion de clients satisfaits des prestations offertes dans la station de ski. Pour cela, il utilise un intervalle de confiance de longueur 0,04 avec un niveau de confiance de 0,95. Le nombre de clients à interroger est :
- 50
- 2500
- 25
- 625
L’amplitude d’un intervalle de confiance au niveau de confiance 0,95 est :
- a=f+1√n−(f−1√n)=2√n.
- On veut donc que 2√n=0,04⟺√n=20,04.
- Donc √n=50 et n=2 500.
Réponse b
Exercice 2 5 points
Le but de cet exercice est d'étudier la suite (un) définie par la donnée de son premier terme u1 et, pour tout entier naturel n supérieur ou égal à 1, par la relation: un+1=(n+1)un−1.
Partie A
- Vérifier, en détaillant le calcul, que si u1=0 alors u4=−17.
- Recopier et compléter l'algorithme ci-dessous pour qu'en saisissant préalablement dans U une valeur de u1 il calcule les termes de la suite (un) de u2 à u13. Pour Nallant de 1 à 12 U←Fin Pour
- On a exécuté cet algorithme pour u1=0,7 puis pour u1=0,8. Voici les valeurs obtenues. Pour u1=0,7 Pour u1=0,80,40,60,20,8−0,22,2−210−1359−92412−7373295−663429654−66341296539−7297523261928−875702539143135−113841326508860754 Quelle semble être la limite de cette suite si u1=0,7 ? Et si u1=0,8 ?
Partie B
On considère la suite (In) définie pour tout entier naturel n, supérieur ou égal à 1, par : In=∫10xne1−xdx. On rappelle que le nombre e est la valeur de la fonction exponentielle en 1, c'est-à-dire que e =e1.
- Prouver que la fonction F définie sur l'intervalle [0~;~1] par F(x)=(−1−x)e1−x est une primitive sur l'intervalle [0~;~1] de la fonction f définie sur l'intervalle [0~;~1] par f(x)=xe1−x.
- En déduire que I1=e−2.
- On admet que, pour tout entier naturel n supérieur ou égal à 1, on a : In+1=(n+1)In−1. Utiliser cette formule pour calculer I2.
-
- Justifier que, pour tout nombre réel x de l'intervalle [0~;~1] et pour tout entier naturel n supérieur ou égal à 1, on a : 0⩽xne1−x⩽xne.
- Justifier que : ∫10xnedx=en+1.
- En déduire que, pour tout entier naturel n supérieur ou égal à 1, on a : 0⩽In⩽en+1.
- Déterminer limn→+∞In.
Partie C
Dans cette partie, on note n! le nombre défini, pour tout entier naturel n supérieur ou égal à 1, par : 1!=1 2!=2×1 et si n⩾3 : n! =n×(n−1)×…×1 On a ainsi par exemple 3! =3×2×1=3×(2×1)=3×2! 4! =4×3×2×1=4×(3×2×1)=4×3! 8! =8×7×6×5×4×3×2×1=8×(7×6×5×4×3×2×1)=8×7! Et, plus généralement : (n+1)!=(n+1)×n!
- Démontrer par récurrence que, pour tout entier naturel n supérieur ou égal à 1, on a : un=n!(u1−e+2)+In. On rappelle que, pour tout entier naturel n supérieur ou égal à 1, on a : un+1=(n+1)un−1 et In+1=(n+1)In−1.
- On admet que : limn→+∞n!=+∞.
- Déterminer la limite de la suite (un) lorsque u1=0,7.
- Déterminer la limite de la suite (un) lorsque u1=0,8.
Correction de l'exercice 2 (6 points)
Le but de cet exercice est d'étudier la suite (un) définie par la donnée de son premier terme u1 et, pour tout entier naturel n supérieur ou égal à 1, par la relation: un+1=(n+1)un−1.
Partie A
- Vérifier, en détaillant le calcul, que si u1=0 alors u4=−17. Si u1=0 alors :
- u2=(1+1)×u1−1=2×0−1=−1
- u3=(2+1)×u2−1=3×(−1)−1=−4
- u4=(3+1)×u3−1=4×(−4)−1=−17
- Recopier et compléter l'algorithme ci-dessous pour qu'en saisissant préalablement dans U une valeur de u1 il calcule les termes de la suite (un) de u2 à u13. Pour Nallant de 1 à 12 U←Fin Pour On a l’algorithme suivant :
- On a exécuté cet algorithme pour u1=0,7 puis pour u1=0,8. Voici les valeurs obtenues. Pour u1=0,7 Pour u1=0,80,40,60,20,8−0,22,2−210−1359−92412−7373295−663429654−66341296539−7297523261928−875702539143135−113841326508860754 Quelle semble être la limite de cette suite si u1=0,7 ? Et si u1=0,8 ? Si u1=0,7 alors il semblerait que la limite de cette suite soit −∞.
- Pour Nallant de 1 à 12 U←(N+1)×U−1Fin Pour
- Si u1=0,8 alors il semblerait que la limite de cette suite soit +∞.
Partie B
On considère la suite (In) définie pour tout entier naturel n, supérieur ou égal à 1, par : In=∫10xne1−xdx. On rappelle que le nombre e est la valeur de la fonction exponentielle en 1, c'est-à-dire que e =e1.
- Prouver que la fonction F définie sur l'intervalle [0~;~1] par F(x)=(−1−x)e1−x est une primitive sur l'intervalle [0~;~1] de la fonction f définie sur l'intervalle [0~;~1] par f(x)=xe1−x. On calcule F′(x) et on vérifie que F′(x)=f(x).
- En déduire que I1=e−2. On a :
- I1=∫10xe1−xdx=F(1)−F(0)=−2−(−1)e1=e−2
- On admet que, pour tout entier naturel n supérieur ou égal à 1, on a : In+1=(n+1)In−1. Utiliser cette formule pour calculer I2. On a I1=e−2 et
- I2=(1+1)I1−1=2(e−2)−1=2e−5
-
- Justifier que, pour tout nombre réel x de l'intervalle [0 ; 1] et pour tout entier naturel n supérieur ou égal à 1, on a : 0⩽xne1−x⩽xne. On a 0≤x≤1 donc −1≤x≤0 et 0≤1−x≤1
- La fonction exponentielle est strictement croissante sur R.
- Ainsi e0≤e1−x≤e1
- Donc 1≤e1−x≤e
- En multipliant chaque terme de ces inégalités par xn, réel positif, on obtient, pour tout entier naturel n :
- xn≤xne1−x≤xne.
- Puisque x∈[0;1] on a également xn∈[0;1] en particulier xn≥0.
- Par conséquent 0≤xne1−x≤xne.
- Justifier que : ∫10xnedx=en+1. On a, pour tout entier naturel n :
- ∫10xnedx=[xn+1n+1e]10=1n+1n+1e−0n+1n+1e=en+1
- En déduire que, pour tout entier naturel n supérieur ou égal à 1, on a : 0⩽In⩽en+1. On intègre sur l’intervalle [0;1] l’inégalité obtenue à la question
- Ainsi :
- ∫100dx≤∫10xne1−xdx≤∫10xnedx
- Par conséquent 0≤In≤en+1.
- Déterminer limn→+∞In. On a limn→+∞en+1=0 et 0≤In≤en+1.
- D’après le théorème des gendarmes, on a alors limn→+∞In=0.
Partie C
Dans cette partie, on note n! le nombre défini, pour tout entier naturel n supérieur ou égal à 1, par : 1!=1
2!=2×1 et si n⩾3 : n! =n×(n−1)×…×1
On a ainsi par exemple 3! =3×2×1=3×(2×1)=3×2!
4! =4×3×2×1=4×(3×2×1)=4×3!
8! =8×7×6×5×4×3×2×1=8×(7×6×5×4×3×2×1)=8×7!
Et, plus généralement : (n+1)!=(n+1)×n!
- Démontrer par récurrence que, pour tout entier naturel n supérieur ou égal à 1, on a : un=n!(u1−e+2)+In. On rappelle que, pour tout entier naturel n supérieur ou égal à 1, on a : un+1=(n+1)un−1 et In+1=(n+1)In−1.
Initialisation :
- Si n=1 on a :
- 1!(u1−e+2)+I1=u1−e+2+e−2=u1.
- La propriété est vraie au rang 1.
Hérédité :
- Supposons la propriété vraie au rang n où n est un entier naturel non nul. On a alors un=n!(u1−e+2)+In.
- Montrons qu’elle est vraie au rang suivant, c’est-à-dire un+1=(n+1)!(u1−e+2)+In+1.
- un+1=(n+1)un−1=(n+1)n!(u1−e+2)+(n+1)In−1=(n+1)!(u1−e+2)+In+1
- La propriété est donc vraie au rang n+1.
Conclusion :
- La propriété est vraie au rang 1 et est héréditaire.
- Par conséquent, pour tout entier naturel n on a : un=n!(u1−e+2)+In.
- On admet que : limn→+∞n!=+∞.
- Déterminer la limite de la suite (un) lorsque u1=0,7. Si u1=0,7 alors u1−e+2≈−0,018<0.
- Donc limn→+∞n!(u1−e+2)=−∞. De plus limn→+∞In=0 et limn→+∞0=0.
- Donc limn→+∞un=−∞.
- Déterminer la limite de la suite (un) lorsque u1=0,8. Si u1=0,8 alors u1−e+2≈0,082>0.
- Donc limn→+∞n!(u1−e+2)=+∞. De plus limn→+∞In=0 et limn→+∞0=0.
- Donc limn→+∞un=+∞.
Exercice 3 5 points
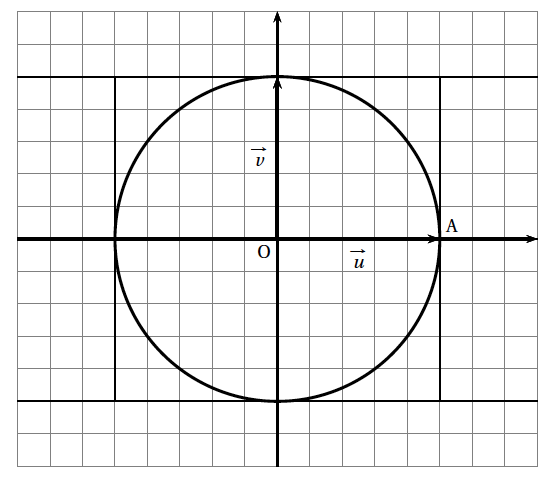
Le plan est muni d'un repère orthonormé direct (O, →u, →v). Le but de cet exercice est de déterminer les nombres complexes z non nuls tels que les points d'affixes 1, z2 et 1z soient alignés. Sur le graphique fourni en annexe, le point A a pour affixe 1.
Partie A: étude d'exemples
- Un premier exemple
Dans cette question, on pose z=i.- Donner la forme algébrique des nombres complexes z2 et 1z.
- Placer les points N1 d'affixe z2, et P1 d'affixe 1z sur le graphique donné en annexe. On remarque que dans ce cas les points A, N1 et P1 ne sont pas alignés.
- Une équation
Résoudre dans l'ensemble des nombres complexes l'équation d’inconnue z : z2+z+1=0. - Un deuxième exemple
Dans cette question, on pose : z=−12+i√32.- Déterminer la forme exponentielle de z, puis celles des nombres complexes z2 et 1z.
- Placer les points N2 d'affixe z2 et P2, d’affixe 1z sur le graphique donné en annexe. On remarque que dans, ce cas les points A, N2 et P2 sont alignés.
Partie B
Soit z un nombre complexe non nul. On note N le point d’affixe z2 et P le point d’affixe 1z.
- Établir que, pour tout nombre complexe différent de 0, on a : z2−1z=(z2+z+1)(1−1z).
- On rappelle que si, →U est un vecteur non nul et →V un vecteur d’affixes respectives z→U et z→V, les vecteurs →U et →V sont colinéaires si et seulement si il existe un nombre réel k tel que z→V=kz→U. En déduire que, pour z≠0, les points A, N et P définis ci-dessus sont alignés si et seulement si z2+z+1 est un réel.
- On pose z=x+iy, où x et y désignent des nombres réels. Justifier que : z2+z+1=x2−y2+x+1+i(2xy+y).
-
- Déterminer l'ensemble des points M d'affixe z≠0 tels que les points A, N et P soient alignés.
- Tracer cet ensemble de points sur le graphique donné en annexe.
Correction de l'exercice 3 (5 points)
Le plan est muni d'un repère orthonormé direct (O, →u, →v). Le but de cet exercice est de déterminer les nombres complexes z non nuls tels que les points d'affixes 1, z2 et 1z soient alignés. Sur le graphique fourni en annexe, le point A a pour affixe 1.
Partie A: étude d'exemples
- Un premier exemple
Dans cette question, on pose z=i.- Donner la forme algébrique des nombres complexes z2 et 1z. z2=i2=−1
- 1z=1i=1i×ii=i−1=−i.
- Placer les points N1 d'affixe z2, et P1 d'affixe 1z sur le graphique donné en annexe. On remarque que dans ce cas les points A, N1 et P1 ne sont pas alignés.
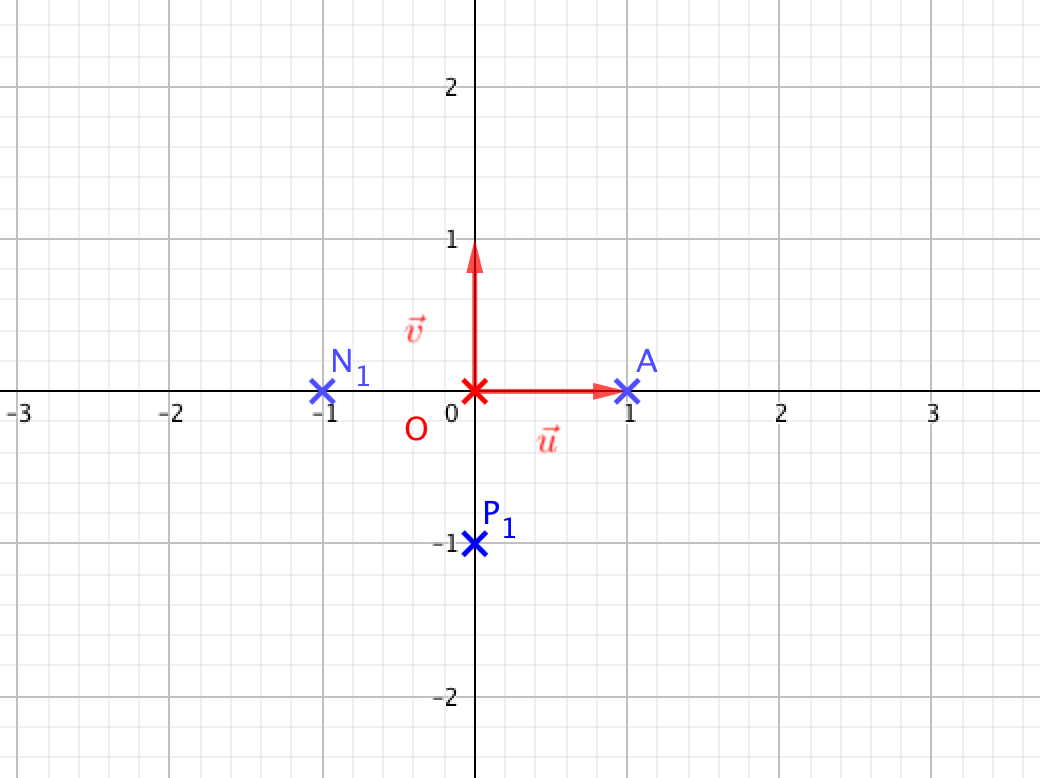
- L’affixe du vecteur →AN1 est z→AN1=−2 et celle du vecteur →AP1 est z→AP1=−i−1.
- Ces deux vecteurs ne sont clairement pas colinéaires et les points A,N1 et P1 ne sont pas alignés.
- Une équation
Résoudre dans l'ensemble des nombres complexes l'équation d’inconnue z : z2+z+1=0.
On a l’équation z2+z+1=0
- Δ=12−4×1×1=−3<0.
- Les solutions de cette équation sont donc z1=−1−i√32 et z2=−1+i√32.
- Un deuxième exemple
Dans cette question, on pose : z=−12+i√32.- Déterminer la forme exponentielle de z, puis celles des nombres complexes z2 et 1z. On a |z|=|−12+i√32|=1
- Donc z=e2iπ/3
- Ainsi z2=e2×2iπ/3=e4iπ/3
- et 1z=e−2iπ/3.
- Placer les points N2 d'affixe z2 et P2, d’affixe 1z sur le graphique donné en annexe. On remarque que dans, ce cas les points A, N2 et P2 sont alignés. On obtient le graphique suivant :
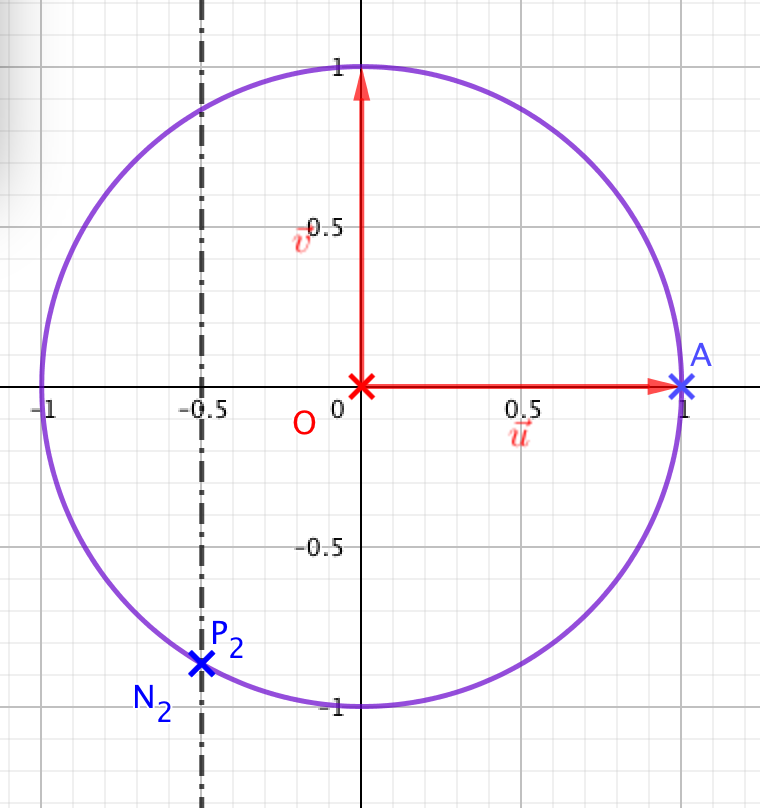
- z2=e4iπ/3=e4iπ/3−2π=e−2iπ/3=1z.
- Les points N2 et P2 sont confondus.
- Par conséquent, les points A,N2 et P2 sont alignés.
Partie B
Soit z un nombre complexe non nul. On note N le point d’affixe z2 et P le point d’affixe 1z.
- Établir que, pour tout nombre complexe différent de 0, on a : z2−1z=(z2+z+1)(1−1z). Pour tout nombre z différent de 0 on a :
- $\begin{align*} \left(z^2+z+1\right)\left(1-\dfrac{1}{z}\right) &=z^2-z+z-1+1-\dfrac{1}{z} \\
- &=z^2-\dfrac{1}{z}\end{align*}$
- On rappelle que si, →U est un vecteur non nul et →V un vecteur d’affixes respectives z→U et z→V, les vecteurs →U et →V sont colinéaires si et seulement si il existe un nombre réel k tel que z→V=kz→U. En déduire que, pour z≠0, les points A, N et P définis ci-dessus sont alignés si et seulement si z2+z+1 est un réel. On considère un nombre complexe z non nul.
- L’affixe du vecteur →PN est z2−1z.
- L’affixe du vecteur →PA est 1−1z.
- Ces deux vecteurs sont colinéaires si, et seulement si, il existe un réel k tel que z2−1z=k(1−1z).
- ⟺(z2+z+1)(1−1z)=k(1−1z)
- ⟺z2+z+1=k ou z=1
- ⟺z2+z+1∈R ou z=1
- ⟺z2+z+1∈R (en effet si z=1 alors z2+z+1=3∈R).
- On pose z=x+iy, où x et y désignent des nombres réels. Justifier que : z2+z+1=x2−y2+x+1+i(2xy+y). Soient x et y des nombres réels et z=x+iy.
- $\begin{align*} z^2+z+1&=(x+\text{i} y)^2+x+\text{i} y+1 \\
- &=x^2+2\text{i} xy-y^2+x+\text{i} y+1\\
- &=x^2-y^2+x+1+\text{i} (2xy+y)\end{align*}$
-
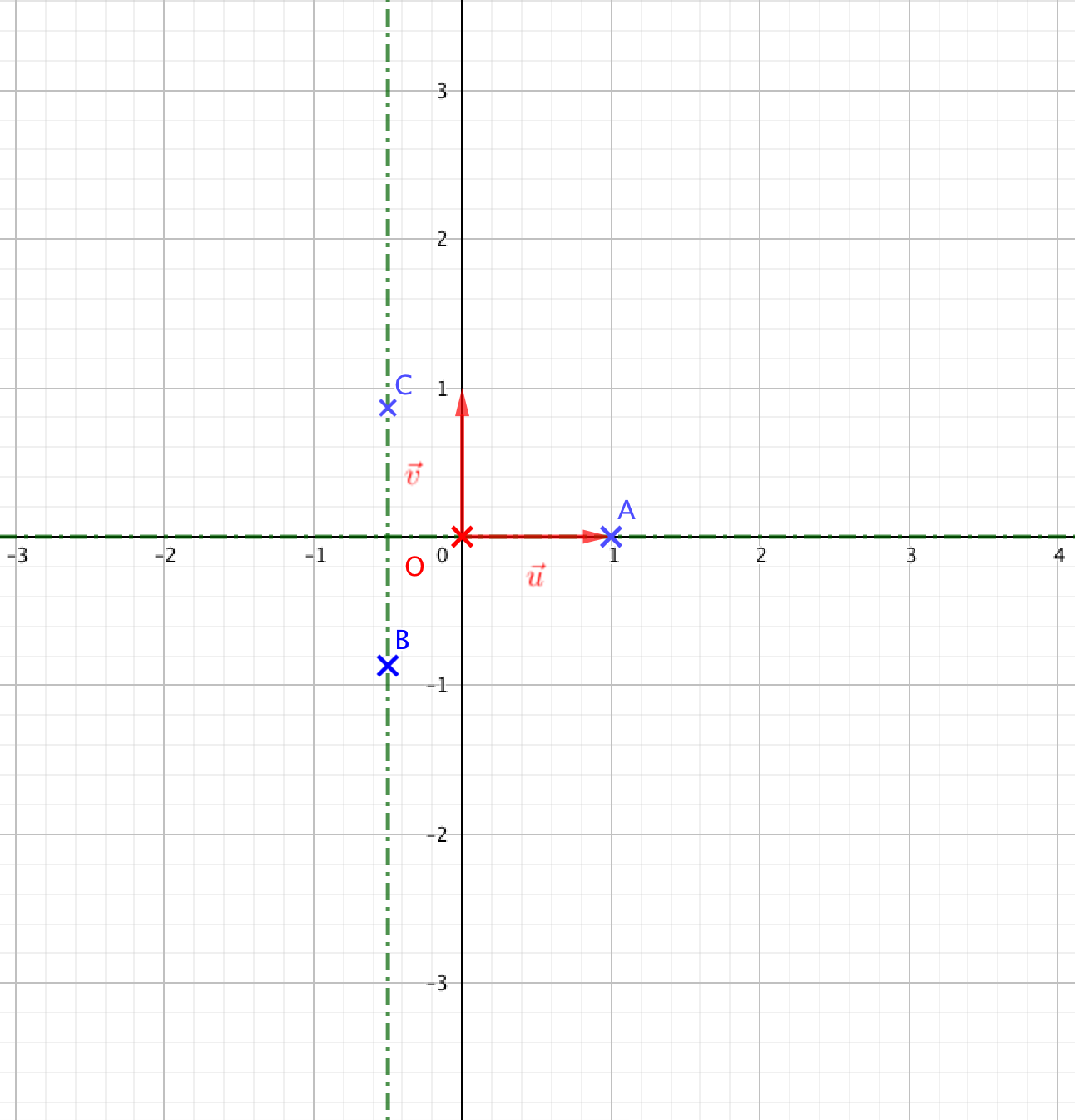
- Déterminer l'ensemble des points M d'affixe z≠0 tels que les points A, N et P soient alignés. z2+z+1 est un réel si, et seulement si, 2xy+y=0
- si, et seulement si, y(2x+1)=0
- si, et seulement si, y=0 ou 2x+1=0
- si, et seulement si, y=0 ou x=−12
- Parmi cet ensemble de solutions, cherchons celles qui annulent également la partie réelle.
- – Si y=0 alors on cherche les solutions de l’équation x2+x+1=0. D’après la question
- elle ne possède pas de solution réelle.
- – Si x=−12 alors on cherche les solutions de l’équation 14−y2−12+1=0 soit y2=34. Cette équation possède deux solutions : −√32 et √32
- Ainsi l’ensemble cherché la réunion des droites d’équation y=0 (l’axe des abscisses) et x=−12 privé des points B et C de coordonnées respectives (−12;−√32) et (−12;√32).
- Tracer cet ensemble de points sur le graphique donné en annexe.
Exercice 4 5 points
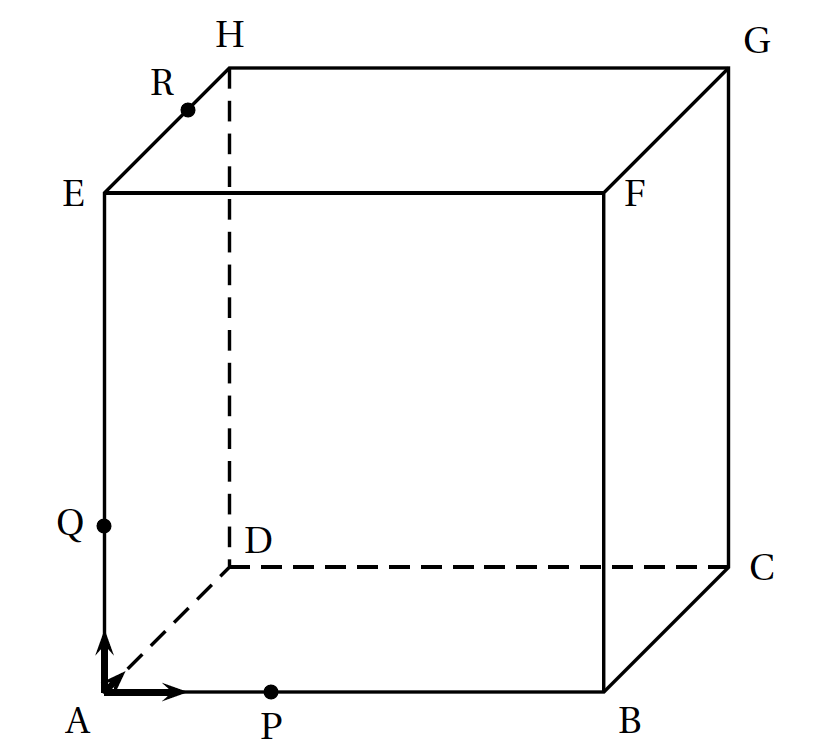
Dans l'espace, on considère un cube ABCDEFGH de centre Ω et d'arête de longueur 6. Les points P, Q et R sont définis par : →AP=13→AB,→AQ=13→AEet→HR=13→HE. Dans tout ce qui suit on utilise le repère orthonormé (A ; →ı, →ȷ,→k) avec : →ı=16→AB,→ȷ=16→ADet→k=16→AE. Dans ce repère, on a par exemple: B(6 ; 0 ; 0),F(6 ; 0 ; 6)et R(0 ; 4 ; 6).
-
- Donner, sans justifier, les coordonnées des points P, Q et Ω.
- Déterminer les nombres réels b et c tels que →n(1 ; b ; c) soit un vecteur normal au plan (PQR) .
- En déduire qu'une équation du plan (PQR) est : x−y+z−2=0.
-
- On note Δ la droite perpendiculaire au plan (PQR) passant par le point Ω, centre du cube. Donner une représentation paramétrique de la droite Δ.
- En déduire que la droite Δ coupe le plan (PQR) au point I de coordonnées (83 ; 103 ; 83).
- Calculer la distance ΩI
- On considère les points J(6 ; 4 ; 0) et K(6 ; 6 ; 2).
- Justifier que le point J appartient au plan (PQR).
- Vérifier que les droites (JK) et (QR) sont parallèles.
- Sur la figure donnée en annexe, tracer la section du cube par le plan (PQR). On laissera apparents les traits de construction, ou bien on expliquera la démarche.
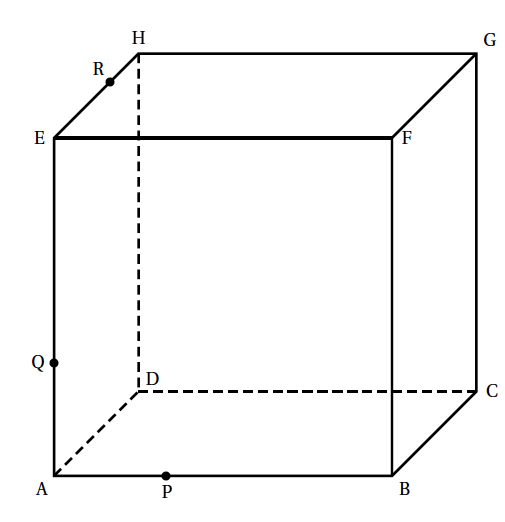
Correction de l'exercice 4 5 points

Dans l'espace, on considère un cube ABCDEFGH de centre Ω et d'arête de longueur 6. Les points P, Q et R sont définis par : →AP=13→AB,→AQ=13→AEet→HR=13→HE. Dans tout ce qui suit on utilise le repère orthonormé (A ; →ı, →ȷ,→k) avec : →ı=16→AB,→ȷ=16→ADet→k=16→AE. Dans ce repère, on a par exemple: B(6 ; 0 ; 0),F(6 ; 0 ; 6)et R(0 ; 4 ; 6).
-
- Donner, sans justifier, les coordonnées des points P, Q et Ω. On a P(2;0;0), Q(0;0;2) et Ω(3;3;3)
- Déterminer les nombres réels b et c tels que →n(1 ; b ; c) soit un vecteur normal au plan (PQR) . On a →PQ(−2;0;2), R(0;4;6) et →PR(−2;4;6).
- Si le vecteur →n est normal au plan (PQR) on a alors :
- →n.→PQ=0⟺−2+0+2c=0⟺c=1 et
- →n.→PR=0⟺−2+4b+6c=0⟺−2+4b+6=0⟺b=−1.
- En déduire qu'une équation du plan (PQR) est : x−y+z−2=0. Le vecteur →n(1;−1;1) est normal au plan (PQR). Une équation cartésienne de ce plan est alors de la forme x−y+z+d=0
- Conclusion : Le vecteur →n(1;−1;1) est normal au plan (PQR).
- Le point P(2;0;0) appartient au plan.
- Donc 2−0+0+d=0⟺d=−2
- Une équation cartésienne du plan (PQR) est donc x−y+z−2=0.
-
- On note Δ la droite perpendiculaire au plan (PQR) passant par le point Ω, centre du cube. Donner une représentation paramétrique de la droite Δ. Le vecteur →n est un vecteur directeur de la droite Δ.
- Une représentation paramétrique de cette droite est donc {x=t+3y=−t+3z=t+3,t∈R
- En déduire que la droite Δ coupe le plan (PQR) au point I de coordonnées (83 ; 103 ; 83). Par définition, le plan (PQR) et la droite Δ sont sécants. Montrons que le point I(83;103;83) appartient à la fois à la droite et au plan.
- Si t=−13 alors : {x=−13+3=83y=13+3=103z=−13+3=83.
- Donc I∈Δ
- $\begin{align*} &\dfrac{8}{3}-\dfrac{10}{3}+\dfrac{8}{3}-2\\
- &=\dfrac{6}{3}-2 \\
- &=0\end{align*}$
- Le point I appartient également au plan (PQR).
- Par conséquent, le point d’intersection de la droite Δ et du plan (PQR) est I(83;103;83).
- Calculer la distance \OmegaI ΩI2=(83−3)2+(103−3)2+(83−3)2=13
- Par conséquent ΩI=1√3=√33.
- On considère les points J(6 ; 4 ; 0) et K(6 ; 6 ; 2).
- Justifier que le point J appartient au plan (PQR). xJ−yJ+zJ−2=6−4+0−2=6−6=0 donc J∈(PQR).
- Vérifier que les droites (JK) et (QR) sont parallèles. On a→JK(0;2;2) et →QR(0;4;4)
- Ainsi →QR=2→JK
- Ces deux vecteurs sont colinéaires. Les droites (JK) et (QR) sont donc parallèles.
- Sur la figure donnée en annexe, tracer la section du cube par le plan (PQR). On laissera apparents les traits de construction, ou bien on expliquera la démarche.
 On place le point J(6;4;0) (on reporte la distance HR à partir de C).
On place le point J(6;4;0) (on reporte la distance HR à partir de C).
- On trace la parallèle à la droite (QR) passant par J. Elle coupe la droite (GC) en K.
- On trace la parallèle à la droite (PJ) passant par R. Elle coupe la droite (HG) en S.
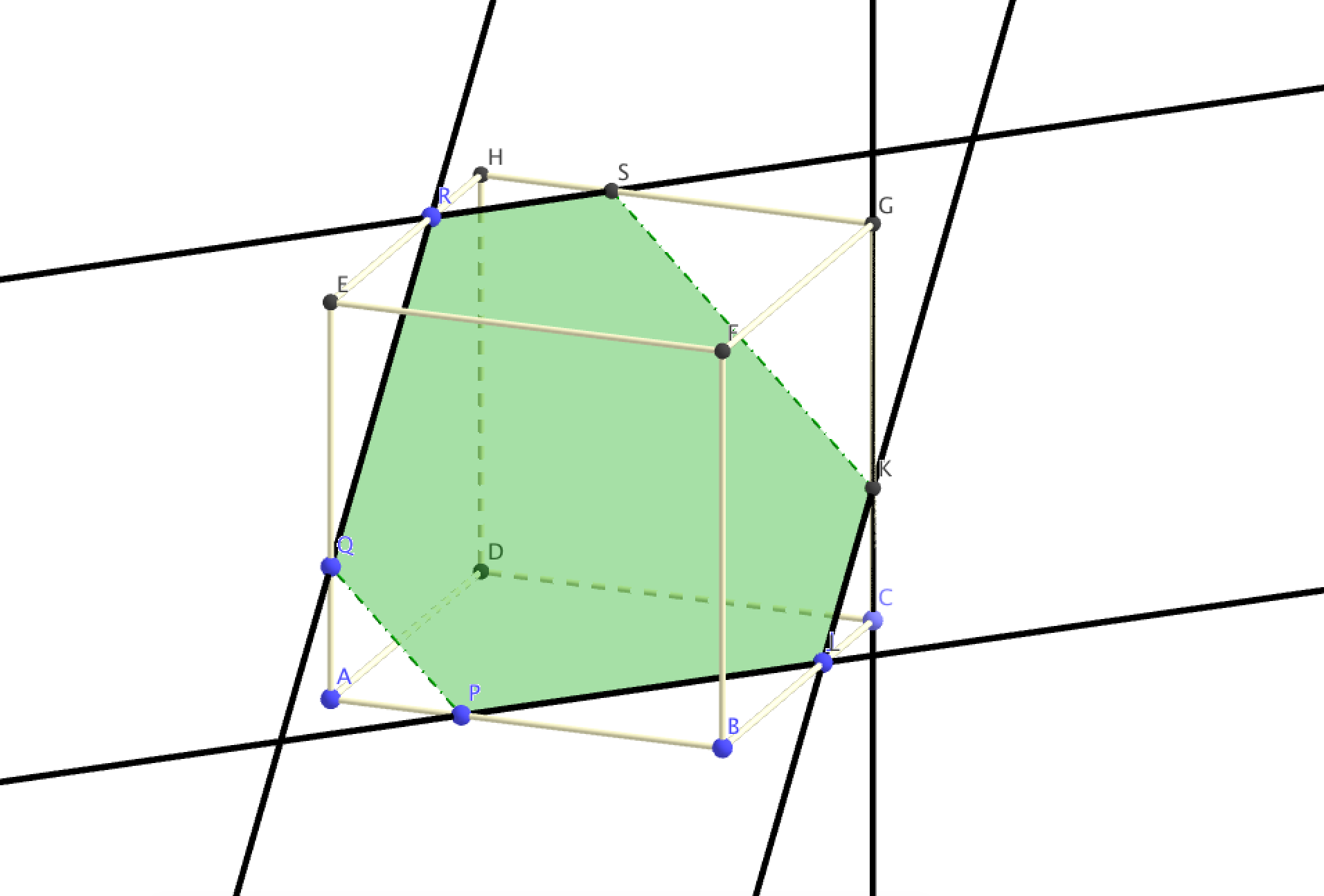
- Pour terminer une figure interactive avec GeoGebra :
Spécialité 5 points
Le but de cet exercice est d'envisager plusieurs décompositions arithmétiques du nombre 40.
Partie A :
Les questions 1., 2. et 3. sont indépendantes
- Sans justifier, donner deux nombres premiers x, et y tels que 40=x+y.
- On considère l'équation 20x+19y=40, où x et y désignent deux, entiers relatifs. Résoudre cette équation.
- Le nombre 40 est une somme de deux carrés puisque : 40=22+62. On veut savoir si 40, est aussi différence de deux carrés, autrement dit s’intéresser à l'équation x2−y2=40, où x et y désignent deux entiers naturels.
- Donner la décomposition de 40 en produit de facteurs premiers.
- Montrer que, si x et y désignent des entiers naturels, les nombres x−y et x+y ont la même parité.
- Déterminer toutes les solutions de l'équation x2−y2=40 où x et y désignent deux entiers naturels.
Partie B : « sommes» de cubes
Les questions 1. et 2. sont indépendantes.
Certains nombres entiers peuvent se décomposer en somme ou différence de cubes d'entiers naturels. Par exemple : 13=43+73+73−93−23 13=−13−13−13+23+23 13=13+73+103−113 Dans tout ce qui suit, on écrira pour simplifier « sommes» de cubes à la place de « sommes ou différence de cubes d'entiers naturels ». Les deux premiers exemples montrent que 13 peut se décomposer en « somme» de 5 cubes. Le troisième exemple montre que 13 peut se décomposer en « somme» de 4 cubes.
-
- En utilisant l'égalité 13=13+73+103−113, donner une décomposition de 40 en « somme » de 5 cubes.
- On admet que pour tout entier naturel n on a : 6n=(n+1)3+(n−1)3−n3−n3 En déduire une décomposition de 48 en « somme» de 4 cubes, puis une décomposition de 40 en « somme» de 5 cubes, différente de celle donnée en 1. a.)
- Le nombre 40 est une « somme» de 4 cubes : 40=43−23−23−23. On veut savoir si 40 peut être décomposé en « somme» de 3 cubes.
- Recopier et compléter sans justifier:
Reste de la division euclidienne de n par 9012345678 Reste de la division euclidienne de n3 par 91 - On déduit du tableau précédent que, pour tout entier naturel n, l'entier naturel n3 est congru modulo 9 soit à 0, soit à 1, soit à −1. Prouver que 40 ne peut pas être décomposé en « somme» de 3 cubes.
- Recopier et compléter sans justifier:
Correction de l'exercice de Spécialité 5 points
Le but de cet exercice est d'envisager plusieurs décompositions arithmétiques du nombre 40.
Partie A :
Les questions 1., 2. et 3. sont indépendantes
- Sans justifier, donner deux nombres premiers x, et y tels que 40=x+y. On a 29+11=40 et les nombres 29 et 11 sont deux nombres premiers.
- On considère l'équation 20x+19y=40, où x et y désignent deux, entiers relatifs. Résoudre cette équation. On a 20×2+19×0=40. Le couple (2;0) est donc solution de l’équation 20x+19y=40.
- On considère un couple solution (x;y) de cette même équation.
- Ainsi 20×2+19×0=40 et 20x+19y=40.
- Par différence on a 20(2−x)+19(−y)=0.
- Soit 20(2−x)=19y.
- 19 et 20 sont premiers entre eux.
- D’après le théorème de Gauss, il existe alors un entier relatif k tel que y=20k et 2−x=19k
- Soit x=2−19k et y=20k.
- Réciproquement, on considère un entier relatif k.
- 20(2−19k)+19×20k=40−380k+380k=40.
- Ainsi la solution de l’équation (20x+19y=40 est l’ensemble des couples (2−19k;20k) pour k∈Z.
- Le nombre 40 est une somme de deux carrés puisque : 40=22+62. On veut savoir si 40, est aussi différence de deux carrés, autrement dit s’intéresser à l'équation x2−y2=40, où x et y désignent deux entiers naturels.
- Donner la décomposition de 40 en produit de facteurs premiers. 40=8×5=23×5
- Montrer que, si x et y désignent des entiers naturels, les nombres x−y et x+y ont la même parité. Supposons que x−y soit pair. Il existe alors un entier relatif k tel que x−y=2k.
- (x−y)+(x+y)=2x soit 2k+x+y=2x.
- Par conséquent x+y=2(x−k) et x+y est pair.
- Supposons maintenant que x−y soit impair. Il existe alors un entier relatif k tel que x−y=2k+1.
- (x−y)+(x+y)=2x soit 2k+1+x+y=2x.
- Par conséquent x+y=2(x−k)−1 et x+y est impair.
- x+y et x−y ont donc la même parité.
- Déterminer toutes les solutions de l'équation x2−y2=40 où x et y désignent deux entiers naturels. x2−y2=40⟺(x+y)(x−y)=23×5.
- Puisque 5 et 23 n’ont pas la même parité, on ne peut pas avoir x+y=5 et x−y=23 ou x+y=23 et x−y=5.
- Pour la même raison, on ne peut pas avoir x+y=1 et x−y=40 ou x+y=40 et x−y=1.
- Les seules possibilités pour les couples (x+y;x−y) sont donc (4;10), (10;4), (2;20) et (20;2).
- {x+y=4x−y=10⟺{x=7y=−3
- {x+y=10x−y=4⟺{x=7y=3
- {x+y=2x−y=20⟺{x=11y=−9
- {x+y=20x−y=2⟺{x=11y=9
- x et y devant être des entiers naturels, les solutions de l’équation x2−y2=40 sont donc les couples (7;3) et (11;9).
Partie B : « sommes» de cubes
Les questions 1. et 2. sont indépendantes.
Certains nombres entiers peuvent se décomposer en somme ou différence de cubes d'entiers naturels. Par exemple : 13=43+73+73−93−23 13=−13−13−13+23+23 13=13+73+103−113 Dans tout ce qui suit, on écrira pour simplifier « sommes» de cubes à la place de « sommes ou différence de cubes d'entiers naturels ». Les deux premiers exemples montrent que 13 peut se décomposer en « somme» de 5 cubes. Le troisième exemple montre que 13 peut se décomposer en « somme» de 4 cubes.
-
- En utilisant l'égalité 13=13+73+103−113, donner une décomposition de 40 en « somme » de 5 cubes. 40=27+13=33+13+73+103−113.
- On admet que pour tout entier naturel n on a : 6n=(n+1)3+(n−1)3−n3−n3 En déduire une décomposition de 48 en « somme» de 4 cubes, puis une décomposition de 40 en « somme» de 5 cubes, différente de celle donnée en 1. a.) On a
- $\begin{align*} 48&=6\times 8 \\
- &=(8+1)^3+(8-1)^3-8^3-8^3\\
- &=9^3+7^3-8^3-8^3\end{align*}$
- Or 40=48−8=93+73−83−83−23
- Le nombre 40 est une « somme» de 4 cubes : 40=43−23−23−23. On veut savoir si 40 peut être décomposé en « somme» de 3 cubes.
- Recopier et compléter sans justifier:
Reste de la division euclidienne de n par 9012345678 Reste de la division euclidienne de n3 par 91
On a :
- Reste de la division euclidienne de n par 9012345678 Reste de la division euclidienne de n3 par 9018018018
- On déduit du tableau précédent que, pour tout entier naturel n, l'entier naturel n3 est congru modulo 9 soit à 0, soit à 1, soit à −1. Prouver que 40 ne peut pas être décomposé en « somme» de 3 cubes. Or 8≡−1 [9] donc, pour tout entier naturel n on a n3 est congru modulo 9 soit à 0, soit à 1 soit à −1.
- Par conséquent, la somme de 3 cubes est congrue modulo 9 appartient à {−3;−2;−1;0;1;2;3}.
- Mais 40≡4 [9].
- Donc 40 ne peut pas être décomposé en « somme »de 3 cubes.
- Recopier et compléter sans justifier:
- Vues: 52841
