Baccalauréat S Liban 29 mai 2018
Exercice 1 3 points
Les quinze jours précédant la rentrée universitaire, le standard téléphonique d'une mutuelle étudiante enregistre un nombre record d'appels. Les appelants sont d'abord mis en attente et entendent une musique d'ambiance et un message préenregistré. Lors de cette première phase, le temps d'attente, exprimé en secondes, est modélisé par la variable aléatoire $X$ qui suit la loi exponentielle de paramètre $\lambda = 0,02$ s$^{-1}$. Les appelants sont ensuite mis en relation avec un chargé de clientèle qui répond à leurs questions. Le temps d'échange, exprimé en secondes, lors de cette deuxième phase est modélisé par la variable aléatoire $Y$, exprimée en secondes, qui suit la loi normale d'espérance $\mu = 96$ s et d'écart-type $\sigma = 26$ s.
- Quelle est la durée totale moyenne d'un appel au standard téléphonique (temps d'attente et temps d'échange avec le chargé de clientèle)?
- Un étudiant est choisi au hasard parmi les appelants du standard téléphonique.
- Calculer la probabilité que l'étudiant soit mis en attente plus de 2 minutes.
- Calculer la probabilité pour que le temps d'échange avec le conseiller soit inférieur à 90 secondes.
- Une étudiante, choisie au hasard parmi les appelants, attend depuis plus d'une minute d'être mise en relation avec le service clientèle. Lasse, elle raccroche et recompose le numéro. Elle espère attendre moins de trente secondes cette fois-ci. Le fait de raccrocher puis de rappeler augmente-t-il ses chances de limiter à $30$ secondes l'attente supplémentaire ou bien aurait-elle mieux fait de rester en ligne ?
Correction de l'exercice 1 (3 points)
Les quinze jours précédant la rentrée universitaire, le standard téléphonique d'une mutuelle étudiante enregistre un nombre record d'appels. Les appelants sont d'abord mis en attente et entendent une musique d'ambiance et un message préenregistré. Lors de cette première phase, le temps d'attente, exprimé en secondes, est modélisé par la variable aléatoire $X$ qui suit la loi exponentielle de paramètre $\lambda = 0,02$ s$^{-1}$. Les appelants sont ensuite mis en relation avec un chargé de clientèle qui répond à leurs questions. Le temps d'échange, exprimé en secondes, lors de cette deuxième phase est modélisé par la variable aléatoire $Y$, exprimée en secondes, qui suit la loi normale d'espérance $\mu = 96$ s et d'écart-type $\sigma = 26$ s.
- Quelle est la durée totale moyenne d'un appel au standard téléphonique (temps d'attente et temps d'échange avec le chargé de clientèle)? L’espérance de la variable aléatoire $X$ est $E(X)=\dfrac{1}{\lambda}=50$.
- Un étudiant est choisi au hasard parmi les appelants du standard téléphonique.
- Calculer la probabilité que l'étudiant soit mis en attente plus de 2 minutes. On veut calculer :
- Calculer la probabilité pour que le temps d'échange avec le conseiller soit inférieur à 90 secondes. On veut calculer :
$P(X \geq 2) = \text{e}^{-2\times 60\lambda} = \text{e}^{-2,4}$
$\quad$
$P(Y\leq 90) = 0,5-P(90 \leq Y \leq 96) \approx 0,409$ ou de façon plus directe :2ND DISTR 2NORMALFRép( -10^(99) , \1,$\2$,$\3$)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(-10^{99},\1,\2,\3) \approx \4$$
$$P( \5 \leq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$ - Une étudiante, choisie au hasard parmi les appelants, attend depuis plus d'une minute d'être mise en relation avec le service clientèle. Lasse, elle raccroche et recompose le numéro. Elle espère attendre moins de trente secondes cette fois-ci. Le fait de raccrocher puis de rappeler augmente-t-il ses chances de limiter à $30$ secondes l'attente supplémentaire ou bien aurait-elle mieux fait de rester en ligne ? On a :
Donc en moyenne, le temps d’attente d’un appel est de $50$ s.
La durée totale moyenne d’un appel au standard téléphonique est donc de $96+50=146$ s soit $2$ min et $26$ s.
$\begin{align*} P_{X > 60}(X<60+30)&=1-P_{X>60}(X>60+30) \\
&=1-P(X>30) \quad (*)\\
&=P(X\leq 30)
\end{align*}$
$(*)$ car la loi exponentielle est à durée de vie sans vieillissement.
Le fait de raccrocher puis de rappeler n’augmente pas (mais ne diminue pas non plus) ses chances de limiter à $30$ secondes l’attente supplémentaire.
$\quad$
Exercice 2 3 points
- Donner les formes exponentielle et trigonométrique des nombres complexes $1 + \text{i}$ et $1 - \text{i}$.
- Pour tout entier naturel $n$, on pose \[S_n = (1 + \text{i})^n + (1 - \text{i})^n.\]
- Déterminer la forme trigonométrique de $S_n$.
- Pour chacune des deux affirmations suivantes, dire si elle est vraie ou fausse en justifiant la réponse. Une réponse non justifiée ne sera pas prise en compte et l'absence de réponse n'est pas pénalisée.
Affirmation A : Pour tout entier naturel $n$, le nombre complexe $S_n$ est un nombre réel.
Affirmation B : Il existe une infinité d'entiers naturels $n$ tels que $S_n = 0$.
Correction de l'exercice 2 (3 points)
- Donner les formes exponentielle et trigonométrique des nombres complexes $1 + \text{i}$ et $1 - \text{i}$. $|1+\text{i}|=\sqrt{2}$
- Pour tout entier naturel $n$, on pose \[S_n = (1 + \text{i})^n + (1 - \text{i})^n.\]
- Déterminer la forme trigonométrique de $S_n$. La formule d’Euler nous permet d’écrire $\cos \theta = \dfrac{\text{e}^{\text{i} \theta}+\text{e}^{\text{i} \theta}}{2}$
- Pour chacune des deux affirmations suivantes, dire si elle est vraie ou fausse en justifiant la réponse. Une réponse non justifiée ne sera pas prise en compte et l'absence de réponse n'est pas pénalisée.
Affirmation A : Pour tout entier naturel $n$, le nombre complexe $S_n$ est un nombre réel.
Affirmation B : Il existe une infinité d'entiers naturels $n$ tels que $S_n = 0$. Affirmation A vraie
$\begin{align*} S_n&=(1+\text{i})^n+(1-\text{i})^n \\
&=\sqrt{2}^n\text{e}^{n\text{i}\pi/4}+\sqrt{2}^n\text{e}^{-n\text{i}\pi/4} \\
&=\sqrt{2}^n \left(\text{e}^{n\text{i}\pi/4}+\text{e}^{-n\text{i}\pi/4}\right) \\
&=\sqrt{2}^n \times 2\times \dfrac{\text{e}^{n\text{i}\pi/4}+\text{e}^{-n\text{i}\pi/4}}{2}\\
&=2\sqrt{2}^n\cos\left(\dfrac{n\pi}{4}\right) \quad(*)
\end{align*}$
$\dfrac{n\pi}{4}$ va prendre les valeurs $0$, $\dfrac{\pi}{4}$, $\dfrac{\pi}{2}$, $\dfrac{3\pi}{4}$, $\pi$, $\dfrac{5\pi}{4}$, $\dfrac{3\pi}{2}$ et $\dfrac{7\pi}{4}$ à $2\pi$ près.
Donc
$\bullet$ si $n$ est de la forme $8k+3$, $8k+4$ ou $8k+5$ alors la forme trigonométrique de $S_n$ est $S_n= 2\sqrt{2}^n\cos\left(\dfrac{n\pi}{4}-\pi\right)\left(\cos \pi+\text{i}\sin \pi\right)$ où $k\in \mathbb{Z}$
$\bullet$ si $n$ est de la forme $8k+2$, $8k+6$ alors $S_n=0$ où $k\in \mathbb{Z}$
$\bullet$ dans les autres cas, la forme trigonométrique de $S_n$ est $S_n=2\sqrt{2}^n\cos\left(\dfrac{n\pi}{4}\right) \left(\cos 0+\text{i}\sin 0\right)$ où $k\in \mathbb{Z}$.
Remarque : La forme $(*)$ n’est pas la forme trigonométrique mais la forme algébrique de $S_n$
$\quad$
D’après la réponse précédente $S_n=2\sqrt{2}^n\cos\left(\dfrac{n\pi}{4}\right) \in \mathbb{R}$.
$\quad$
Affirmation B vraie
si $n$ est de la forme $8k+2$, $8k+6$ alors $S_n=0$ avec $k\in \mathbb{Z}$.
Donc $1+\text{i}=\sqrt{2}\left(\dfrac{\sqrt{2}}{2}+\text{i}\dfrac{\sqrt{2}}{2}\right)=\sqrt{2}\text{e}^{\text{i}\pi/4}$ (forme exponentielle).
On a aussi $1+\text{i}=\sqrt{2}\left(\cos\dfrac{\pi}{4}+\text{i} \sin \dfrac{\pi}{4}\right)$ (forme trigonométrique).
$\quad$
On remarque que $1-\text{i}=\overline{1+\text{i}}=\sqrt{2}\text{e}^{-\text{i}\pi/4}$ (forme exponentielle).
Par conséquent $1-\text{i}=\sqrt{2}\left(\cos \left(-\dfrac{\pi}{4}\right)+\text{i} \sin \left(-\dfrac{\pi}{4}\right)\right)$ (forme trigonométrique).
$\quad$
Exercice 3 4 points
L'objectif de cet exercice est d'étudier les trajectoires de deux sous-marins en phase de plongée.
On considère que ces sous-marins se déplacent en ligne droite, chacun à vitesse constante.
À chaque instant $t$, exprimé en minutes, le premier sous-marin est repéré par le point $S_1(t)$ et le second sous-marin est repéré par le point $S_2(t)$ dans un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$ dont l'unité est le mètre. 
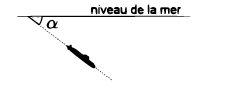
Le plan défini par $\left(\text{O},~\vec{i},~\vec{j}\right)$ représente la surface de la mer. La cote $z$ est nulle au niveau de la mer, négative sous l'eau.
- On admet que, pour tout réel $t \geqslant 0$, le point $S_1(t)$ a pour coordonnées: \[\left\{\begin{array}{l c l} x(t) &=& \phantom{-}140 - 60t\\ y(t) &=& \phantom{-}105 - 90t\\ z(t) &=& -170 - 30 t \end{array}\right.\]
- Donner les coordonnées du sous- marin au début de l'observation.
- Quelle est la vitesse du sous-marin ?
- On se place dans le plan vertical contenant la trajectoire du premier sous-marin. Déterminer l'angle $\alpha$ que forme la trajectoire du sous-marin avec le plan horizontal. On donnera l'arrondi de $\alpha$ à $0,1$ degré près.
- Au début de l'observation, le second sous-marin est situé au point $S_2(0)$ de coordonnées $(68~;~135~;~- 68)$ et atteint au bout de trois minutes le point $S_2(3)$ de coordonnées $(-202~;~-405~;~ - 248)$ avec une vitesse constante. À quel instant $t$, exprimé en minutes, les deux sous-marins sont-ils à la même profondeur ?
Correction de l'exercice 3 (5 points)
L'objectif de cet exercice est d'étudier les trajectoires de deux sous-marins en phase de plongée.
On considère que ces sous-marins se déplacent en ligne droite, chacun à vitesse constante.
À chaque instant $t$, exprimé en minutes, le premier sous-marin est repéré par le point $S_1(t)$ et le second sous-marin est repéré par le point $S_2(t)$ dans un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$ dont l'unité est le mètre. 
Le plan défini par $\left(\text{O},~\vec{i},~\vec{j}\right)$ représente la surface de la mer. La cote $z$ est nulle au niveau de la mer, négative sous l'eau.
- On admet que, pour tout réel $t \geqslant 0$, le point $S_1(t)$ a pour coordonnées: \[\left\{\begin{array}{l c l} x(t) &=& \phantom{-}140 - 60t\\ y(t) &=& \phantom{-}105 - 90t\\ z(t) &=& -170 - 30 t \end{array}\right.\]
- Donner les coordonnées du sous- marin au début de l'observation. Quand $t=0$ alors le sous-marin a pour coordonnées $A(140,105,-170)$.
- Quelle est la vitesse du sous-marin ? Le vecteur vitesse du sous marin est $\vec{V_1}(-60;-90;-30)$.
- On se place dans le plan vertical contenant la trajectoire du premier sous-marin. Déterminer l'angle $\alpha$ que forme la trajectoire du sous-marin avec le plan horizontal. On donnera l'arrondi de $\alpha$ à $0,1$ degré près.
 On considère le point $B(80,15,-200)$ quand $t=1$ et le point $C(80,15,-170)$.
On considère le point $B(80,15,-200)$ quand $t=1$ et le point $C(80,15,-170)$.
$\quad$
La vitesse du sous-marin est donc $v_1=\sqrt{(-60)^2+(-90)^2+(-30)^2}$ $=\sqrt{12~600}$ $=30\sqrt{14}$.
$\quad$
Le plan $(ABC)$ correspond donc au plan vertical contenant la trajectoire du premier sous-marin.
On a alors $\vec{AB}(-60;-90;-30)$ et $\vec{AC}(-60;-90;0)$.
Donc $AB=\sqrt{12~600}$ et $AC=\sqrt{11~700}$
D’une part $\vec{AB}.\vec{AC}=-60\times (-60)+(-90)\times (-90)+0=11~700$.
D’autre part $\vec{AB}.\vec{AC}=\sqrt{12~600}\times \sqrt{11~700}\cos \alpha$.
Ainsi $\cos \alpha =\dfrac{11~700}{\sqrt{12~600}\times \sqrt{11~700}}=\dfrac{\sqrt{11~700}}{\sqrt{12~600}}$
Par conséquent $\alpha \approx 15,5$°
$\quad$ - Au début de l'observation, le second sous-marin est situé au point $S_2(0)$ de coordonnées $(68~;~135~;~- 68)$ et atteint au bout de trois minutes le point $S_2(3)$ de coordonnées $(-202~;~-405~;~ - 248)$ avec une vitesse constante. À quel instant $t$, exprimé en minutes, les deux sous-marins sont-ils à la même profondeur ? La vitesse du second sous-marin est constante.
Par conséquent le point $S_2(t)$ a pour coordonnées :
$$\begin{cases} x(t)=68+at\\y(t)=135+bt\\z(t)=-68+ct\end{cases}$$
On sait que $S_2(3)$ a pour coordonnées $(-202;-405;-248)$.
Ainsi
$\begin{cases} 68+3a=-202\\135+3b=-405\\-68+3t=-248\end{cases} \iff \begin{cases} a=-90\\b=-180\\c=-60\end{cases}$.
le point $S_2(t)$ a pour coordonnées :
$$\begin{cases} x(t)=68-90t\\y(t)=135-180t\\z(t)=-68-60t\end{cases}$$
$\quad$
Les deux sous-marins sont à la même profondeur quand :
$-170-30t=-68-60t \iff 30t=102 \iff t=3,4$
Les deux sous-marins sont à la même profondeur au bout de $3$ min $24$ s.
$\quad$
Exercice 4 5 points
On considère, pour tout entier $n > 0$, les fonctions $f_n$ définies sur l'intervalle $[1~;~5] $par: \[f_n(x) = \dfrac{\ln x}{x^n}.\] . Pour tout entier $n > 0$, on note $\mathcal{C}_n$ la courbe représentative de la fonction $f_n$ dans un repère orthogonal. Sur le graphique ci-dessous sont représentées les courbes $\mathcal{C}_n$ pour $n$ appartenant à $\{1~;~2~;~3~;~4\}$.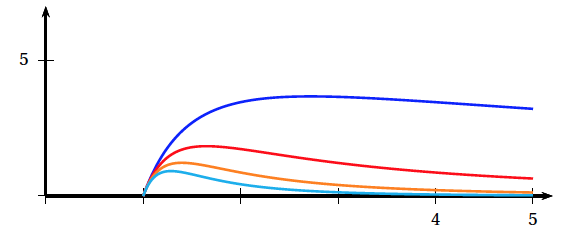
- Montrer que, pour tout entier $n > 0$ et tout réel $x$ de l'intervalle $[1~;~5] $: \[f'_n(x) = \dfrac{1- n\ln (x)}{x^{n+1}}.\]
- Pour tout entier $n > 0$, on admet que la fonction $f_n$ admet un maximum sur l'intervalle [1~;~5]. On note $A_n$ le point de la courbe $\mathcal{C}_n$ ayant pour ordonnée ce maximum. Montrer que tous les points $A_n$ appartiennent à une même courbe $\Gamma$ d'équation \[y = \dfrac{1}{\text{e}} \ln (x).\]
-
- Montrer que, pour tout entier $n > 1$ et tout réel $x$ de l'intervalle $[1~;~5] $: \[0 \leqslant \dfrac{\ln (x)}{x^n} \leqslant \dfrac{\ln (5)}{x^n}.\]
- Montrer que pour tout entier $n > 1$ : \[\displaystyle\int_1^5 \dfrac{1}{x^n} \:\text{d}x = \dfrac{1}{n - 1}\left(1 - \dfrac{1}{5^{n - 1}} \right).\]
- Pour tout entier $n > 0$, on s'intéresse à l'aire, exprimée en unités d'aire, de la surface sous la courbe $f_n$, c'est-à-dire l'aire du domaine du plan délimité par les droites d'équations $x = 1$, $x = 5$, $y = 0$ et la courbe $\mathcal{C}_n$. Déterminer la valeur limite de cette aire quand $n$ tend vers $+ \infty$.
Correction Exercice 4 5 points
On considère, pour tout entier $n > 0$, les fonctions $f_n$ définies sur l'intervalle $[1~;~5] $par: \[f_n(x) = \dfrac{\ln x}{x^n}.\] . Pour tout entier $n > 0$, on note $\mathcal{C}_n$ la courbe représentative de la fonction $f_n$ dans un repère orthogonal. Sur le graphique ci-dessous sont représentées les courbes $\mathcal{C}_n$ pour $n$ appartenant à $\{1~;~2~;~3~;~4\}$.
- Montrer que, pour tout entier $n > 0$ et tout réel $x$ de l'intervalle $[1~;~5] $: \[f'_n(x) = \dfrac{1- n\ln (x)}{x^{n+1}}.\] Pour entier naturel $n$ non nul, la fonction $f_n$ est dérivable sur l’intervalle $[1;5]$ en tant que quotient de fonctions dérivables dont le dénominateur ne s’annule pas.
- Pour tout entier $n > 0$, on admet que la fonction $f_n$ admet un maximum sur l'intervalle [1~;~5]. On note $A_n$ le point de la courbe $\mathcal{C}_n$ ayant pour ordonnée ce maximum. Montrer que tous les points $A_n$ appartiennent à une même courbe $\Gamma$ d'équation \[y = \dfrac{1}{\text{e}} \ln (x).\] Pour tout entier naturel $n$ non nul, le maximum est atteint quand $f’_n(x)=0$
-
- Montrer que, pour tout entier $n > 1$ et tout réel $x$ de l'intervalle $[1~;~5] $: \[0 \leqslant \dfrac{\ln (x)}{x^n} \leqslant \dfrac{\ln (5)}{x^n}.\] La fonction $\ln$ est strictement croissante sur l’intervalle $[1;5]$.
- Montrer que pour tout entier $n > 1$ : \[\displaystyle\int_1^5 \dfrac{1}{x^n} \:\text{d}x = \dfrac{1}{n - 1}\left(1 - \dfrac{1}{5^{n - 1}} \right).\] $\begin{align*} \displaystyle \int_1^5 \dfrac{1}{x^n}\:\text{d}x &=\int_1^5 x^{-n}\:\text{d}x \\
- Pour tout entier $n > 0$, on s'intéresse à l'aire, exprimée en unités d'aire, de la surface sous la courbe $f_n$, c'est-à-dire l'aire du domaine du plan délimité par les droites d'équations $x = 1$, $x = 5$, $y = 0$ et la courbe $\mathcal{C}_n$. Déterminer la valeur limite de cette aire quand $n$ tend vers $+ \infty$. Pour tout entier naturel $n$ non nul, la fonction $f_n$ est positive sur l’intervalle $[1;5]$ comme quotient de fonction positive sur cet intervalle.
par conséquent :
$\begin{align*} 1\leq x\\5 &\iff \ln(1) \leq \ln(x) \leq \ln(5) \\
&\iff 0 \leq \ln(x) \leq \ln(5) \\
&\iff 0\leq \dfrac{\ln(x)}{x^n}\leq \dfrac{\ln(5)}{x^n}
\end{align*}$
$\quad$
&=\left[\dfrac{x^{-n+1}}{-n+1}\right]_1^5 \\
&=\dfrac{5^{-n+1}-1^{-n+1}}{-n+1} \\
&=\dfrac{1-5^{-n+1}}{n-1} \\
&=\dfrac{1}{n-1}\left(1-\dfrac{1}{5^{n-1}}\right)
\end{align*}$
$\quad$
Ainsi l’aire cherchée est $I_n=\displaystyle \int_1^5 \dfrac{1}{x^n}\:\text{d}x $.
Or, d’après la question précédente $I_n=\dfrac{1}{n-1}\left(1-\left(\dfrac{1}{5}\right)^{n-1}\right)$
On a $-1<\dfrac{1}{5}<1$ donc $\lim\limits_{n \to +\infty}\left(\dfrac{1}{5}\right)^{n-1} = 0$.
De plus $\lim\limits_{n \to +\infty} \dfrac{1}{n-1}=0$.
Donc $\lim\limits_{n \to +\infty} I_n=0$.
$\quad$
$\begin{align*} f’_n(x)&=\dfrac{\dfrac{1}{x}x^n-nx^{n-1}\ln(x)}{x^{2n}} \\
&=\dfrac{x^{n-1}-nx^{n-1}\ln(x)}{x^{2n}} \\
&=\dfrac{x^{n-1}\left(1-n\ln(x)\right)}{x^{2n}} \\
&=\dfrac{1-n\ln(x)}{x^{n+1}}
\end{align*}$
$\iff 1-n\ln(x)=0$
$\iff \ln(x)=\dfrac{1}{n}$
$\iff x=\text{e}^{1/n}$
L’ordonnée du maximum est alors :
$\begin{align*} f_n\left(\text{e}^{1/n}\right)&=\dfrac{~~\dfrac{1}{n}~~}{\text{e}^{n\times 1/n}} \\
&=\dfrac{~~\dfrac{1}{n}~~}{ \text{e}} \\
&=\dfrac{\ln\left(\text{e}^{1/n}\right)}{\text{e}}
\end{align*}$
Les points $A_n$ appartiennent donc à la courbe $\Gamma$.
Exercice 5 : 5 points
Un jeu de hasard sur ordinateur est paramétré de la façon suivante :
- Si le joueur gagne une partie, la probabilité qu'il gagne la partie suivante est $\dfrac{1}{4}$ ;
- Si le joueur perd une partie, la probabilité qu'il perde la partie suivante est $\dfrac{1}{2}$ ;
- La probabilité de gagner la première partie est $\dfrac{1}{4}$ .
Pour tout entier naturel $n$ non nul, on note $G_n$ l'évènement " la $n^\text{e}$ partie est gagnée " et on note $p_n$ la probabilité de cet évènement. On a donc $p_1 = \dfrac{1}{4}$.
- Montrer que $p_2 = \dfrac{7}{16}$.
- Montrer que, pour tout entier naturel $n$ non nul, $p_{n+1} = - \dfrac{1}{4}p_n + \dfrac{1}{2}$.
- On obtient ainsi les premières valeurs de $p_n$ : $$\begin{array} {|c|c|c|c|c|c|c|c|}\hline n &1 &2 &3 &4 &5 &6 &7\\ \hline p_n & 1 & 0,4375 & 0,3906 & 0,4023 & 0,3994 & 0,4001 & 0,3999 \\ \hline \end{array}$$ Quelle conjecture peut -on émettre ?
- On définit, pour tout entier naturel $n$ non nul, la suite $\left(u_n\right)$ par $u_n = p_n - \dfrac{2}{5}$.
- Démontrer que la suite $\left(u_n\right)$ est une suite géométrique dont on précisera la raison.
- En déduire que, pour tout entier naturel $n$ non nul, $p_n = \dfrac{2}{5} - \dfrac{3}{20}\left(- \dfrac{1}{4}\right)^{n-1}$.
- La suite $\left(p_n\right)$ converge-t-elle ? Interpréter ce résultat.
Correction de l'exercice 5 5 points
Un jeu de hasard sur ordinateur est paramétré de la façon suivante :
- Si le joueur gagne une partie, la probabilité qu'il gagne la partie suivante est $\dfrac{1}{4}$ ;
- Si le joueur perd une partie, la probabilité qu'il perde la partie suivante est $\dfrac{1}{2}$ ;
- La probabilité de gagner la première partie est $\dfrac{1}{4}$ .
Pour tout entier naturel $n$ non nul, on note $G_n$ l'évènement " la $n^\text{e}$ partie est gagnée " et on note $p_n$ la probabilité de cet évènement. On a donc $p_1 = \dfrac{1}{4}$.
- Montrer que $p_2 = \dfrac{7}{16}$. On utilise l'arbre pondéré ci-dessous :
- Montrer que, pour tout entier naturel $n$ non nul, $p_{n+1} = - \dfrac{1}{4}p_n + \dfrac{1}{2}$. On utilise l'arbre pondéré ci-dessous :
- On obtient ainsi les premières valeurs de $p_n$ : $$\begin{array} {|c|c|c|c|c|c|c|c|}\hline n &1 &2 &3 &4 &5 &6 &7\\ \hline p_n & 1 & 0,4375 & 0,3906 & 0,4023 & 0,3994 & 0,4001 & 0,3999 \\ \hline \end{array}$$ Quelle conjecture peut -on émettre ? Il semblerait que la limite de la suite $\left(p_n\right)$ soit $0,4$.
- On définit, pour tout entier naturel $n$ non nul, la suite $\left(u_n\right)$ par $u_n = p_n - \dfrac{2}{5}$.
- Démontrer que la suite $\left(u_n\right)$ est une suite géométrique dont on précisera la raison. Pour tout entier naturel $n$ non nul on a $u_n=p_n-\dfrac{2}{5}$ soit $p_n=u_n+\dfrac{2}{5}$.
- En déduire que, pour tout entier naturel $n$ non nul, $p_n = \dfrac{2}{5} - \dfrac{3}{20}\left(- \dfrac{1}{4}\right)^{n-1}$. Ainsi, pour tout entier naturel $n$ non nul, on a $u_n=-\dfrac{3}{20}\left(-\dfrac{1}{4}\right)^{n-1}$.
- La suite $\left(p_n\right)$ converge-t-elle ? Interpréter ce résultat. On a $-1<-\dfrac{1}{4}<1$ donc $\lim\limits_{n \to +\infty} \left(-\dfrac{1}{4}\right)^{n-1}=0$.
$\begin{align*} u_{n+1}&=p_{n+1}-\dfrac{2}{5} \\
&=-\dfrac{1}{4}p_n+\dfrac{1}{2}-\dfrac{2}{5} \\
&=-\dfrac{1}{4}\left(u_n+\dfrac{2}{5}\right)+\dfrac{1}{10} \\
&=-\dfrac{1}{4}u_n-\dfrac{1}{10}+\dfrac{1}{10} \\
&=-\dfrac{1}{4}u_n
\end{align*}$
La suite $\left(u_n\right)$ est donc géométrique de raison $-\dfrac{1}{4}$ et de premier terme $u_1=p_1-\dfrac{2}{5}=-\dfrac{3}{20}$.
$\quad$
Or $p_n=u_n+\dfrac{2}{5}=-\dfrac{3}{20}\left(-\dfrac{1}{4}\right)^{n-1}+\dfrac{2}{5}$.
$\quad$
Donc la suite $\left(p_n\right)$ converge vers $\dfrac{2}{5}=0,4$.
Sur le long terme, la probabilité qu’un joueur gagne une partie est $0,4$.
$\quad$
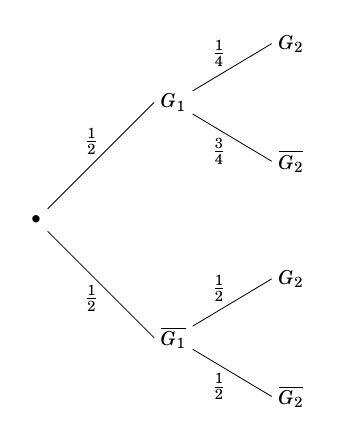
D’après la formule des probabilités totales on a :
$\begin{align*} p_2&=p\left(G_2\right) \\
&=p\left(G_1\cap G_2\right)+p\left(\overline{G_1}\cap G_2\right) \\
&=\dfrac{1}{4}\times \dfrac{1}{4}+\dfrac{3}{4}\times \dfrac{1}{2} \\
&=\dfrac{7}{16}
\end{align*}$
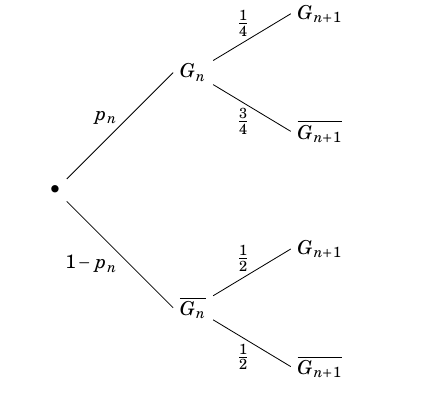
’après la formule des probabilités totales on a :
$\begin{align*} p_{n+1}&=p\left(G_{n+1}\right) \\
&=p\left(G_n\cap G_{n+1}\right)+p\left(\overline{G_n}\cap G_{n+1}\right) \\
&=\dfrac{1}{4}\times p_n+\dfrac{1}{2}\times \left(1-p_n\right) \\
&=\dfrac{p_n}{4}+\dfrac{1}{2}-\dfrac{p_n}{2} \\
&=-\dfrac{1}{4}p_n+\dfrac{1}{2}
\end{align*}$
$\quad$
Spécialité 5 points
On définit la suite de réels $\left(a_n\right)$ par : \[\left\{\begin{array}{l c l} a_0 &= &0\\ a_1 &= &1\\ a_{n+1} &=& a_n + a_{n-1}\: \text{ pour }\: n \geqslant 1. \end{array}\right.\] On appelle cette suite la suite de Fibonacci.
- Recopier et compléter l'algorithme ci-dessous pour qu'à la fin de son exécution la variable $A$ contienne le terme $a_n$. $$\begin{array}{|c c|}\hline 1&A \gets 0\\ 2& B \gets 1\\ 3& \text{Pour } i \text{ allant de 2 à } n :\\ 4& \hspace{0.4cm} C \gets A + B \\ 5& \hspace{0.4cm} A \gets \ldots \\ 6& \hspace{0.4cm} B \gets \ldots \\ 7& \text{Fin Pour}\\ \hline \end{array} $$ On obtient ainsi les premières valeurs de la suite $a_n$ : $$ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline n &0 &1 &2 &3 &4 &5 &6 &7 &8 &9 &10\\ \hline a_n &0 & 1 &1 &2 &3 &5 &8 &13 &21 &34 &55\\ \hline \end{array} $$
- Soit la matrice $A = \begin{pmatrix}1&1\\1&0\end{pmatrix}$. Calculer $A^2$, $A^3$ et $A^4$. Vérifier que $A^5 = \begin{pmatrix}8&5\\5&3\end{pmatrix}$.
- On peut démontrer, et nous admettrons, que pour tout entier naturel $n$ non nul, \[A^n = \begin{pmatrix}a_{n+1}&a_n\\a_n&a_{n-1}\end{pmatrix}.\]
- Soit $p$ et $q$ deux entiers naturels non nuls. Calculer le produit $A^p \times A^q$ et en déduire que \[a_{p+q} = a_p \times a_{q+1} + a_{p-1} \times a_q.\]
- En déduire que si un entier $r$ divise les entiers $a_p$ et $a_q$, alors $r$ divise également $a_{p+q}$.
- Soit $p$ un entier naturel non nul. Démontrer, en utilisant un raisonnement par récurrence sur $n$, que pour tout entier naturel $n$ non nul, $a_p$ divise $a_{np}$.
-
- Soit $n$ un entier supérieur ou égal à 5. Montrer que si $n$ est un entier naturel qui n'est pas premier, alors $a_n$ n'est pas un nombre premier.
- On peut calculer $a_{19} = 4181 = 37 \times 113$. Que penser de la réciproque de la propriété obtenue dans la question 4. a. ?
Correction de l'exercice de Spécialité 5 points
On définit la suite de réels $\left(a_n\right)$ par : \[\left\{\begin{array}{l c l} a_0 &= &0\\ a_1 &= &1\\ a_{n+1} &=& a_n + a_{n-1}\: \text{ pour }\: n \geqslant 1. \end{array}\right.\] On appelle cette suite la suite de Fibonacci.
- Recopier et compléter l'algorithme ci-dessous pour qu'à la fin de son exécution la variable $A$ contienne le terme $a_n$. $$\begin{array}{|c c|}\hline 1&A \gets 0\\ 2& B \gets 1\\ 3& \text{Pour } i \text{ allant de 2 à } n :\\ 4& \hspace{0.4cm} C \gets A + B \\ 5& \hspace{0.4cm} A \gets \ldots \\ 6& \hspace{0.4cm} B \gets \ldots \\ 7& \text{Fin Pour}\\ \hline \end{array} $$ On obtient ainsi les premières valeurs de la suite $a_n$ : $$ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline n &0 &1 &2 &3 &4 &5 &6 &7 &8 &9 &10\\ \hline a_n &0 & 1 &1 &2 &3 &5 &8 &13 &21 &34 &55\\ \hline \end{array} $$ On obtient l’algorithme suivant :
- Soit la matrice $A = \begin{pmatrix}1&1\\1&0\end{pmatrix}$. Calculer $A^2$, $A^3$ et $A^4$. Vérifier que $A^5 = \begin{pmatrix}8&5\\5&3\end{pmatrix}$. On a $A=\begin{pmatrix}1&1\\1&0\end{pmatrix}$
- On peut démontrer, et nous admettrons, que pour tout entier naturel $n$ non nul, \[A^n = \begin{pmatrix}a_{n+1}&a_n\\a_n&a_{n-1}\end{pmatrix}.\]
- Soit $p$ et $q$ deux entiers naturels non nuls. Calculer le produit $A^p \times A^q$ et en déduire que \[a_{p+q} = a_p \times a_{q+1} + a_{p-1} \times a_q.\] On a $A^p\times A^q=A^{p+q}$
- En déduire que si un entier $r$ divise les entiers $a_p$ et $a_q$, alors $r$ divise également $a_{p+q}$. Si $r$ divise $a_p$ et $a_q$ alors :
- Soit $p$ un entier naturel non nul. Démontrer, en utilisant un raisonnement par récurrence sur $n$, que pour tout entier naturel $n$ non nul, $a_p$ divise $a_{np}$. Initialisation : Si $n=1$ alors $a_{np}=a_p$. $a_p$ divise donc $a_{np}$
$A^p=\begin{pmatrix} a_{p+1}&a_p\\a_p&a_{p-1}\end{pmatrix}$
$A^q=\begin{pmatrix} a_{q+1}&a_p\\a_q&a_{q-1}\end{pmatrix}$
Dans le produit $A_p\times A_q$ on regarde le terme situé sur la deuxième ligne et la première colonne.
Ainsi $a_{p+q}=a_p\times a_{q+1}+a_{p-1}\times a_q$.
$\quad$
$a_p\times a_{q+1} \equiv 0~~[r]$ et $a_{p-1}\times a_q\equiv 0~~[r]$.
Donc, par somme, $a_{p+q}\equiv 0~~[r]$.
$r$ divise également $a_{p+q}$.
$\quad$
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$ non nul : $a_p$ divise $a_{np}$.
alors $a_{(n+1)p}=a_{np+p}$
$a_p$ divise $a_p$ et $a_{np}$ donc, d’après la question précédente, $a_p$ divise également $a_{(n+1)p}$.
$\quad$
Conclusion : La propriété est vraie au rang $1$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ non nul, $a_p$ divise $a_{np}$.
$\quad$ -
- Soit $n$ un entier supérieur ou égal à 5. Montrer que si $n$ est un entier naturel qui n'est pas premier, alors $a_n$ n'est pas un nombre premier. Si $n$ est un entier naturel supérieur ou égal à $5$ qui n’est pas premier alors il existe deux entiers naturels non nul $p$ et $q$ tels que $n=pq$.
- On peut calculer $a_{19} = 4181 = 37 \times 113$. Que penser de la réciproque de la propriété obtenue dans la question 4. a. ? La réciproque de la propriété obtenue à la question 4.a. est “Soit $n$ un entier naturel supérieur ou égal à $5$. Si $a_n$ n’est pas un nombre premier alors $n$ n’est pas un nombre premier.
Ainsi d’après la question précédente $a_p$ divise $a_{pq}=a_n$.
Par conséquent $a_n$ n’est pas un nombre premier.
$\quad$
Or $a_{19}$ n’est pas un nombre premier alors que $19$ l’est.
La réciproque est donc fausse.
$\quad$
$$\begin{array}{|c c|}\hline 1&A \gets 0\\ 2& B \gets 1\\ 3& \text{Pour } i \text{ allant de 2 à } n :\\ 4& \hspace{0.4cm} C \gets A + B \\ 5& \hspace{0.4cm} A \gets B \\ 6& \hspace{0.4cm} B \gets C \\ 7& \text{Fin Pour}\\ \hline \end{array} $$ On obtient ainsi les premières valeurs de la suite $a_n$ : $$ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|}\hline n &0 &1 &2 &3 &4 &5 &6 &7 &8 &9 &10\\ \hline a_n &0 & 1 &1 &2 &3 &5 &8 &13 &21 &34 &55\\ \hline \end{array} $$
Remarque : la valeur de départ $i=2$ donnée par l’énoncé est fausse. Il faut en effet que la boucle commence à $i=1$ pour que l’algorithme réponde précisément à la question posée. Une autre alternative serait par exemple de faire varier la variable $i$ de $2$ à $n+1$.
$\quad$
Donc $A^2=\begin{pmatrix} 1+1&1+0\\1+0&1+0\end{pmatrix}=\begin{pmatrix}2&1\\1&1\end{pmatrix}$
$A^3=\begin{pmatrix}2+1&1+1\\2+0&1+0\end{pmatrix}=\begin{pmatrix}3&2\\2&1\end{pmatrix}$
$A^4=\begin{pmatrix}5+2&2+1\\3+0&2+0\end{pmatrix}=\begin{pmatrix}5&3\\3&2\end{pmatrix}$
$A^5=\begin{pmatrix}5+3&3+2\\5+0&3+0\end{pmatrix}=\begin{pmatrix}8&5\\5&3\end{pmatrix}$.
$\quad$
- Vues: 39337
