Baccalauréat S Amérique du Nord 29 mai 2018 - Spécialité

Page 9 sur 10: Spécialité

Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Dans une région, on s'intéresse à la cohabitation de deux espèces animales : les campagnols et les renards, les renards étant les prédateurs des campagnols.
Au 1er juillet 2012, on estime qu'il y a dans cette région approximativement deux millions de campagnols et cent-vingt renards.
On note $u_n$ le nombre de campagnols et $v_n$ le nombre de renards au 1er juillet de l'année $2012+ n$.

Partie A - Un modèle simple

On modélise l'évolution des populations par les relations suivantes : $$\left\{\begin{array}{l c r} u_{n+1}& =& 1,1u_n - 2000 v_n\\ v_{n+1} & =& 2 \times 10^{-5}u_n + 0,6v_n \end{array}\right. \quad \text{pour tout entier }\:n \geqslant 0,\: \text{avec } \:u_0 = 2000000 \: \text{et} \: v_0 = 120.$$

1. 1. On considère la matrice colonne $U_n = \begin{pmatrix}u_n\\v_n\end{pmatrix}$ pour tout entier $n \geqslant 0$. Déterminer la matrice $A$ telle que $U_{n+1} = A \times U_n$ pour tout entier $n$ et donner la matrice $U_0$.
   2. Calculer le nombre de campagnols et de renards estimés grâce à ce modèle au 1er juillet 2018.
2. Soit les matrices $P = \begin{pmatrix} 20000 & 5000 \\1&1\end{pmatrix} , \: D = \begin{pmatrix}1&0\\0&0,7\end{pmatrix}$ et $P^{- 1} = \dfrac{1}{ 15000} \begin{pmatrix}1& -5000 \\- 1& 20000 \end{pmatrix}$. On admet que $P^{- 1}$ est la matrice inverse de la matrice $P$ et que $A = P \times D \times P^{- 1}$.
   1. Montrer que pour tout entier naturel $n$, $U_n = P \times D^n \times P^{- 1} \times U_0$.
   2. Donner sans justification l'expression de la matrice $D^n$ en fonction de $n$.
   3. On admet que, pour tout entier naturel $n$ : $$\left\{\begin{array}{l c r} u_n &=& \dfrac{2,8 \times 10^7 + 2 \times 10^6 \times 0,7^n}{15}\\ v_n &=&\dfrac{ 1400 + 400 \times 0,7^n}{15} \end{array}\right.$$ Décrire l'évolution des deux populations.

 

Partie B - Un modèle plus conforme à la réalité

Dans la réalité, on observe que si le nombre de renards a suffisamment baissé, alors le nombre de campagnols augmente à nouveau, ce qui n'est pas le cas avec le modèle précédent. On construit donc un autre modèle, plus précis, qui tient compte de ce type d'observations à l'aide des relations suivantes : $$\left\{\begin{array}{l c r} u_{n+1} &=& 1,1u_n - 0,001 u_n \times v_n\\ v_{n+1} &=& 2 \times 10^{-7} u_n \times v_n + 0,6v_n \end{array}\right.\quad \text{pour tout entier }\:n \geqslant 0,\: \text{avec }\:u_0 = 2000000 \: \text{et }\: v_0 = 120.$$
Le tableau ci-dessous présente ce nouveau modèle sur les $25$ premières années en donnant les effectifs des populations arrondis à l'unité :

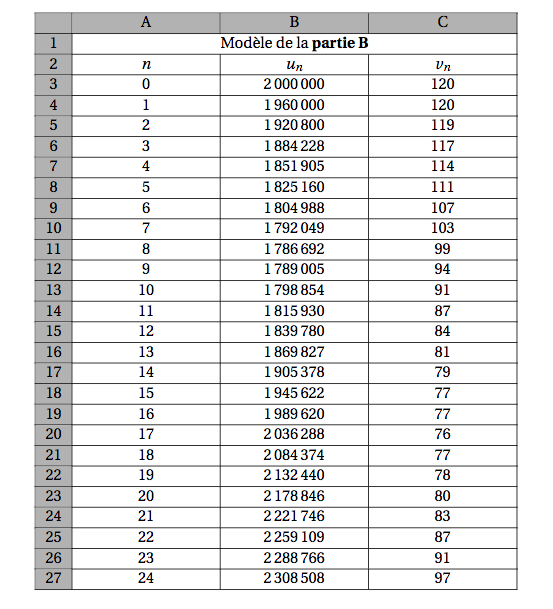
1. Quelles formules faut-il écrire dans les cellules B4 et C4 et recopier vers le bas pour remplir les colonnes B et C ?
2. Avec le deuxième modèle, à partir de quelle année observe-t-on le phénomène décrit (baisse des renards et hausse des campagnols) ?

 

Partie C

Dans cette partie on utilise le modèle de la partie B. Est - il possible de donner à $u_0$ et $v_0$ des valeurs afin que les deux populations restent stables d'une année sur l'autre, c'est-à-dire telles que pour tout entier naturel $n$ on ait $u_{n+1} = u_n$ et $v_{n+1} = v_n$ ? (On parle alors d'état stable.)