Baccalauréat S Amérique du Nord 29 mai 2018 - Correction Exercice 1

Page 2 sur 10: Correction Exercice 1

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

On étudie certaines caractéristiques d'un supermarché d'une petite ville.

Partie A - Démonstration préliminaire

Soit $X$ une variable aléatoire qui suit la loi exponentielle de paramètre $0,2$. On rappelle que l'espérance de la variable aléatoire $X$, notée $E(X)$, est égale à: \[\displaystyle\lim_{x \to + \infty}\int_{0}^{x} 0,2t\text{e}^{-0,2t}\:\text{d}t.\] Le but de cette partie est de démontrer que $E(X) = 5$.

1. On note $g$ la fonction définie sur l'intervalle $[0 ; +\infty[$ par $g(t) = 0,2t\text{e}^{-0,2t}$. On définit la fonction $G$ sur l'intervalle $[0 ; +\infty[$ par $G(t) = (- t - 5)\text{e}^{-0,2t}$. Vérifier que $G$ est une primitive de $g$ sur l'intervalle $[0 ; +\infty[$.
La fonction $G$ est dérivable sur l’intervalle $[0;+\infty[$ comme produit de fonctions dérivables sur cet intervalle.
$\begin{align*} G'(t)&=-\text{e}^{-0,2t}-0,2(-t-5)\text{e}^{-0,2t} \\
&=(-1+0,2t+1)\text{e}^{-0,2t} \\
&=0,2t\text{e}^{-0,2t} \\
&=g(t)
\end{align*}$
La fonction $G$ est bien une primitive de la fonction $g$ sur l’intervalle $[0;+\infty[$.
$\quad$
2. En déduire que la valeur exacte de $E(X)$ est 5.
   Indication : on pourra utiliser, sans le démontrer, le résultat suivant : \[\displaystyle\lim_{x \to + \infty} x \text{e}^{- 0,2x} = 0.\]
On a :
$\displaystyle \int_0^x 0,2t\text{e}^{-0,2t}\:\text{d}t =G(x)-G(0)=-x\text{e}^{-0,2x}-5\text{e}^{-0,2x}+5$.
Or $\lim\limits_{x \to +\infty} x\text{e}^{-0,2x}=0$.
De plus $\lim\limits_{x\to +\infty} -0,2x=-\infty$ et $\lim\limits_{X \to -\infty} \text{e}^X = 0$ donc $\lim\limits_{x\to +\infty}e^{-0,2x}=0$.
Ainsi $E(X)=\lim\limits_{x\to +\infty} x\text{e}^{-0,2x}-5\text{e}^{-0,2x}+5=5$.

 

Partie B - Étude de la durée de présence d'un client dans le supermarché

Une étude commandée par le gérant du supermarché permet de modéliser la durée, exprimée en minutes, passée dans le supermarché par un client choisi au hasard par une variable aléatoire $T$. Cette variable $T$ suit une loi normale d'espérance $40$ minutes et d'écart type un réel positif noté $\sigma$. Grâce à cette étude, on estime que $P(T < 10) = 0,067$.

1. Déterminer une valeur arrondie du réel $\sigma$ à la seconde près.
La variable aléatoire $Z=\dfrac{X-40}{\sigma}$ suit la loi normale centrée réduite.
$\begin{align*} P(T<10)=0,067&\iff P(T-40<-30)=0,067 \\
&\iff P\left(\dfrac{T-40}{\sigma}<-\dfrac{30}{\sigma}\right)=0,067 \\
& \iff P\left(Z<-\dfrac{30}{\sigma}\right)=0,067
\end{align*}$
À l’aide de la calculatrice, on trouve $-\dfrac{30}{\sigma}\approx -1,476$
Donc $\sigma \approx 20$.

2. Dans cette question, on prend $\sigma = 20$ minutes. Quelle est alors la proportion de clients qui passent plus d'une heure dans le supermarché ?
On veut calculer :
$P(T>60)=0,5-P(40<T<60) \approx 0,159$.
Environ $15,9\%$ des clients passent plus d’une heure dans le supermarché.
$\quad$

 

Partie C - Durée d'attente pour le paiement

Ce supermarché laisse le choix au client d'utiliser seul des bornes automatiques de paiement ou bien de passer par une caisse gérée par un opérateur.

1. La durée d'attente à une borne automatique, exprimée en minutes, est modélisée par une variable aléatoire qui suit la loi exponentielle de paramètre $0,2$ min$^{-1}$.
   1. Donner la durée moyenne d'attente d'un client à une borne automatique de paiement.
   $E(X)=\dfrac{1}{\lambda}=5$.
   En moyenne un client attend $5$ min à une borne automatique.
   
   2. Calculer la probabilité, arrondie à $10^{-3}$, que la durée d'attente d'un client à une borne automatique de paiement soit supérieure à $10$ minutes.
   $P(T>10)=\text{e}^{-0,2\times 10}=\text{e}^{-2}\approx 0,135$.
   La probabilité que la durée d’attente d’un client à une borne automatique de paiement soit supérieure à $10$ minutes est environ égal à $0,135$.
   $\quad$
2. L'étude commandée par le gérant conduit à la modélisation suivante:
   • parmi les clients ayant choisi de passer à une borne automatique, 86 % attendent moins de $10$ minutes ;
   • parmi les clients passant en caisse, 63 % attendent moins de $10$ minutes.
   
   On choisit un client du magasin au hasard et on définit les évènements suivants :
   $B$ : « le client paye à une borne automatique » ;
   $\overline{B}$ : « le client paye à une caisse avec opérateur » ;
   $S$ : « la durée d'attente du client lors du paiement est inférieure à $10$ minutes ». Une attente supérieure à dix minutes à une caisse avec opérateur ou à une borne automatique engendre chez le client une perception négative du magasin. Le gérant souhaite que plus de 75 % des clients attendent moins de $10$ minutes. Quelle est la proportion minimale de clients qui doivent choisir une borne automatique de paiement pour que cet objectif soit atteint ?
On appelle $x$ la probabilité qu’un client choisissent une borne automatique de paiement.

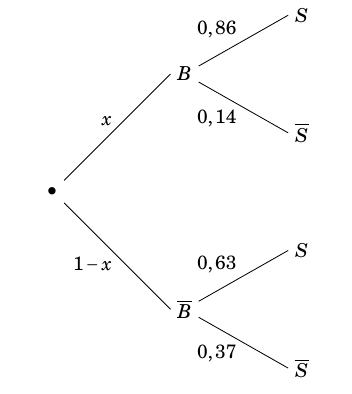
D’après la formule des probabilités totales on a :
$\begin{align*} p(S) \geq 0,75&\iff p(S\cap B)+p\left( S\cap \overline{B}\right) \\
&\iff 0,86x+0,63(1-x)\geq 0,75 \\
&\iff 0,23x \geq 0,12 \\
&\iff x \geq \dfrac{12}{23}
\end{align*}$
Il faut donc que la proportion minimale de clients qui doivent choisir une borne automatique de paiement pour que l’objectif soit atteint est donc $\dfrac{12}{23}$.

 

Partie D - Bons d'achat

Lors du paiement, des cartes à gratter, gagnantes ou perdantes, sont distribuées aux clients. Le nombre de cartes distribuées dépend du montant des achats. Chaque client a droit à une carte à gratter par tranche de $10$ € d'achats. Par exemple, si le montant des achats est 58,64 €, alors le client obtient $5$ cartes ; si le montant est 124,31 €, le client obtient $12$ cartes. Les cartes gagnantes représentent $0,5$ % de l'ensemble du stock de cartes. De plus, ce stock est suffisamment grand pour assimiler la distribution d'une carte à un tirage avec remise.

1. Un client effectue des achats pour un montant de 158,02 €. Quelle est la probabilité, arrondie à $10^{-2}$, qu'il obtienne au moins une carte gagnante ?
On appelle $C$ la variable aléatoire comptant le nombre de cartes gagnantes.
Le client effectue pour $158,02$ € d’achats. Il obtient donc $15$ cartes.
On effectue donc $15$ tirages aléatoires, identiques, indépendants. Chaque tirage possède deux issues : $G$, “la carte est gagnante”, et $\overline{G}$.
De plus $p(G)=0,005$.
La variable aléatoire $C$ suit donc la loi binomiale de paramètres $n=15$ et $p=0,005$.
Ainsi $P(C\geq 1)=1-P(C=0)=1-(1-0,005)^{15} \approx 0,07$.
$\quad$
2. À partir de quel montant d'achats, arrondi à 10 €, la probabilité d'obtenir au moins une carte gagnante est-elle supérieure à 50 % ?
On appelle $D$ la variable aléatoire comptant le nombre de cartes gagnantes.
On effectue $n$ tirages aléatoires, identiques, indépendants. Chaque tirage possède deux issues : $G$, “la carte est gagnante”, et $\overline{G}$.
De plus $p(G)=0,005$.
La variable aléatoire $D$ suit donc la loi binomiale de paramètres $n$ et $p=0,005$.
$\begin{align*} P(D\geq 1)>0,5 &\iff 1-(1-0,005)^n > 0,5 \\
&\iff 0,995^n<0,5 \\
&\iff n\ln(0,995)<\ln (0,5) \\
&\iff n>\dfrac{\ln (0,5)}{\ln(0,995)}
\end{align*}$
Or $\dfrac{\ln(0,5)}{\ln(0,995)} \approx 138,3$.
Il faut donc que $n \geq 139$.
Cela signifie que le montant d’achats soit supérieur à $1~390$ €.