Baccalauréat S Centres étrangers 11 juin 2018 - Correction Exercice 1
Correction de l'exercice 1 (4 points)
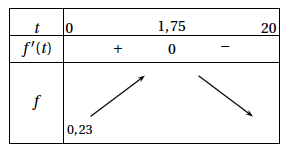
Dans une usine, on se propose de tester un prototype de hotte aspirante pour un local industriel. Avant de lancer la fabrication en série, on réalise l'expérience suivante : dans un local clos équipé du prototype de hotte aspirante, on diffuse du dioxyde de carbone (CO$_2$) à débit constant. Dans ce qui suit, $t$ est le temps exprimé en minute. À l'instant $t = 0$, la hotte est mise en marche et on la laisse fonctionner pendant $20$ minutes. Les mesures réalisées permettent de modéliser le taux (en pourcentage) de CO$_2$ contenu dans le local au bout de $t$ minutes de fonctionnement de la hotte par l'expression $f(t)$, où $f$ est la fonction définie pour tout réel $t$ de l'intervalle $[0~;~20]$ par : \[f(t) = (0,8t + 0,2)\text{e}^{-0,5t} + 0,03.\] On donne ci-dessous le tableau de variation de la fonction $f$ sur l'intervalle $[0~;~20]$. Ainsi, la valeur $f(0) = 0,23$ traduit le fait que le taux de CO$_2$ à l'instant $0$ est égal à 23 %.
- Dans cette question, on arrondira les deux résultats au millième.
- Calculer $f (20)$. $f(20)=(16+0,2)\text{e}^{-10}+0,03=16,2\text{e}^{-10}+0,03 \approx 0,031$
- Déterminer le taux maximal de CO$_2$ présent dans le local pendant l'expérience. La fonction $f$ admet, d’après le tableau de variation un maximum pour $t=1,75$.
$\quad$
$f(1,75)=1,6\text{e}^{-0,875}+0,03\approx 0,697$.
Le taux maximal de CO$_2$ est donc d’environ $69,7\%$. - On souhaite que le taux de CO$_2$ dans le local retrouve une valeur $V$ inférieure ou égale à $3,5$ %.
- Justifier qu'il existe un unique instant $T$ satisfaisant cette condition. Sur l’intervalle $[0;1,75]$ la fonction $f$ est strictement croissante. On a donc $f(t) \geqslant 0,23 > 0,035$.
- On considère l'algorithme suivant : $$ \begin{array} {|l |}\hline t \gets 1,75 \\ p \gets 0,1 \\ V \gets 0,7 \\ \text{Tant que } V > 0,035 \\ \hspace{0.75cm} t \gets t + p \\ \hspace{0.75cm} V \gets (0,8t + 0,2)\text{e}^{-0,5t} + 0,03 \\ \text{Fin Tant que}\\ \hline \end{array} $$ Quelle est la valeur de la variable $t$ à la fin de l'algorithme ? Que représente cette valeur dans le contexte de l'exercice ? À l’aide de la calculatrice on trouve que la variable $t$ à la fin de l’algorithme vaut $15,75$.
L’équation $f(x)=0,035$ ne possède donc pas de solution sur cet intervalle.
$\quad$
Sur l’intervalle $[1,75;20]$, la fonction $f$ est continue et strictement décroissante.
De plus $f(1,75)\approx 0,697 > 0,035$ et $f(20)\approx 0,031<0,035$.
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation $f(x)=0,035$ possède une unique solution $T$ sur l’intervalle $[1,75;20]$.
Par conséquent, l’équation $f(t)=0,035$ possède une unique solution sur l’intervalle $[0;20]$.
$\quad$
Cela signifie qu’il faut attendre $15$ minutes et $45$ secondes pour obtenir un taux de CO$_2$ inférieur ou égal à $3,5\%$.
$\quad$ - On désigne par $V_m$ le taux moyen ( en pourcentage) de CO$_2$ présent dans le local pendant les Il premières minutes de fonctionnement de la hotte aspirante.
- Soit $F$ la fonction définie sur l'intervalle $[0~;~11]$ par : \[F(t) = (-1,6t -3,6)\text{e}^{-0,5t} +0,03t.\] Montrer que la fonction $F$ est une primitive de la fonction $f$ sur l'intervalle $[0~;~11]$. La fonction $F$ est dérivable sur l’intervalle $[0;11]$ comme somme, produit et composée de fonctions dérivables sur cet intervalle.
- En déduire le taux moyen $V_m$, valeur moyenne de la fonction $f$ sur l'intervalle $[0~;~11]$. Arrondir le résultat au millième, soit à $0,1$ %. On a :
Pour tout réel $x$ de l’intervalle $[0;11]$ on a :
$\begin{align*} F'(t)&=-1,6\text{e}^{-0,5t}-0,5(-1,6t-3,6)\text{e}^{-0,5t}+0,03 \\
&=(-1,6+0,8t+1,8)\text{e}^{-0,5t}+0,03\\
&=(0,8t+0,2)\text{e}^{-0,5t}+0,03\\
&=f(t)
\end{align*}$
La fonction $F$ est donc une primitive de la fonction $f $sur l’intervalle $[0;11]$.
$\quad$
$\begin{align*} V_m&=\dfrac{1}{11-0}\displaystyle \int_0^{11} f(t)\;\text{d} t \\
&=\dfrac{1}{11}\left[F(11)-F(0)\right] \\
&=\dfrac{-21,2\text{e}^{-5,5}+0,33+3,6}{11}\\
&=\dfrac{-21,2\text{e}^{-5,5}+3,93}{11}\\
&\approx 0,349
\end{align*}$
Le taux moyen $V_m$ est donc envion égal à $34,9\%$.
- Vues: 24746
