Baccalauréat S Métropole 22 juin 2018 - Correction Exercice 1
Page 2 sur 10
Correction de l'exercice 1 (6 points)
Dans cet exercice, on munit le plan d'un repère orthonormé.
On a représenté ci-dessous la courbe d'équation: \[y = \dfrac{1}{2}\left(\text{e}^x + \text{e}^{-x} - 2\right).\] Cette courbe est appelée une « chaînette ». On s'intéresse ici aux « arcs de chaînette» délimités par deux points de cette courbe symétriques par rapport à l'axe des ordonnées. Un tel arc est représenté sur le graphique ci-dessous en trait plein. On définit la « largeur » et la « hauteur » de l'arc de chaînette délimité par les points $M$ et $M'$ comme indiqué sur le graphique. 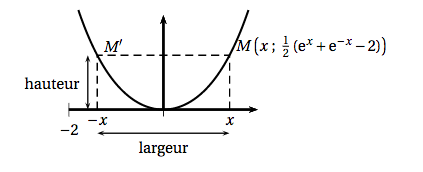
Le but de l'exercice est d'étudier les positions possibles sur la courbe du point $M$ d'abscisse $x$ strictement positive afin que la largeur de l'arc de chaînette soit égale à sa hauteur.
- Justifier que le problème étudié se ramène à la recherche des solutions strictement positives de l'équation \[(E) : \text{e}^x + \text{e}^{- x} - 2 = 0.\] La largeur de la chaînette est $MM’=2x$.
- On note $f$ la fonction définie sur l'intervalle $[0~;~ +\infty[$ par : \[f(x) = \text{e}^x + \text{e}^{- x} - 4x - 2.\]
- Vérifier que pour tout $x > 0,\: f(x) = x \left(\dfrac{\text{e}^x}{x}- 4\right) + \text{e}^{- x} - 2$. $x\left(\dfrac{\text{e}^x}{x}-4\right)+\text{e}^{-x}-2 =\text{e}^x-4x+\text{e}^{-x}-2=f(x)$.
- Déterminer $\displaystyle\lim_{x \to + \infty} f(x)$. $\lim\limits_{x \to +\infty} -x=-\infty$ et $\lim\limits_{X \to -\infty} \text{e}^X=0$
$\quad$
Donc $\lim\limits_{x \to +\infty} \text{e}^{-x}=0$.
De plus $\lim\limits_{x \to +\infty} \dfrac{\text{e}^x}{x}=+\infty$ donc $\lim\limits_{x \to +\infty} x\left(\dfrac{\text{e}^x}{x}-4\right)=+\infty$.
Par conséquent $\lim\limits_{x \to +\infty} f(x)=+\infty$.
$\quad$ -
- On note $f'$ la fonction dérivée de la fonction $f$. Calculer $f'(x)$, où $x$ appartient à l'intervalle $[0~;~ +\infty[$. La fonction $f$ est dérivable sur l’intervalle $[0;+\infty[$ comme somme de fonctions dérivables sur cet intervalle.
- Montrer que l'équation $f'(x) = 0$ équivaut à l'équation : $\left(\text{e}^x\right)^2 - 4\text{e}^x - 1 = 0$. $\begin{align*} f'(x)=0 &\iff \text{e}^x-\text{e}^{-x}-4=0 \\
- En posant $X = \text{e}^x$, montrer que l'équation $f'(x) = 0$ admet pour unique solution réelle le nombre $\ln \left(2 + \sqrt{5}\right)$. On pose $X=\text{e}^x$.
$f'(x)=\text{e}^x-\text{e}^{-x}-4$.
$\quad$
&\iff \dfrac{\text{e}{2x}-1-4\text{e}^x}{\text{e}^x}=0 \\
&\iff \dfrac{\left(\text{e}^x\right)^2-4\text{e}^x-1}{\text{e}^x}=0
&\iff \left(\text{e}^x\right)^2-4\text{e}^x-1=0 \quad \text{car } \text{e}^x >0 \text{ sur } [0;+\infty[
\end{align*}$
$\quad$
On a alors
$ \left(\text{e}^x\right)^2-4\text{e}^x-1=0 \iff \begin{cases} X=\text{e}^x\\X^2-4X-1=0 \end{cases} $
Calculons le discriminant du polynôme $X^2-4X-1$
$\Delta = (-4)^2-4\times 1\times (-1)=20>0$
Il possède donc deux racines réelles : $X_1=\dfrac{4-\sqrt{20}}{2}=2-\sqrt{5} <0$
et $X_2=\dfrac{4+\sqrt{20}}{2}=2+\sqrt{5}>0$.
Ainsi :
$\begin{cases} X=\text{e}^x\\X^2-4X-1=0 \end{cases} \iff \begin{cases} X=\text{e}^x \\X=2-\sqrt{5} \text{ou } X=2+\sqrt{5}\end{cases}$
$X_1<0$ donc la seule solution possible est celle qui vérifie $2+\sqrt{5}=\text{e}^x \iff x=\ln \left(2+\sqrt{5}\right)$.
$\quad$ - On donne ci-dessous le tableau de signes de la fonction dérivée $f'$ de $f$ :
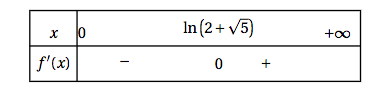
- Dresser le tableau de variations de la fonction $f$. On obtient le tableau de variation suivant :
- Démontrer que l'équation $f(x) = 0$ admet une unique solution strictement positive que l'on notera $\alpha$. $f$ est strictement décroissante sur l'intervalle $\left]0; \ln \left(2+\sqrt{5}\right)\right[$;
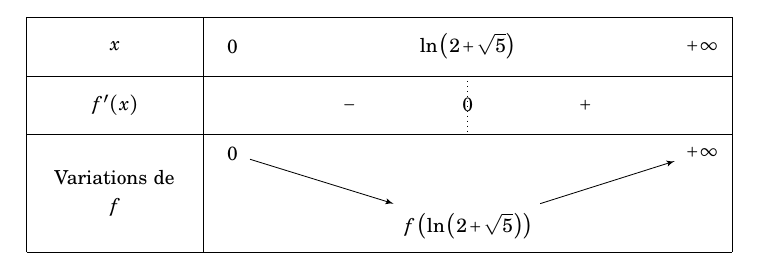
On a $f\left(\ln \left(2+\sqrt{5}\right)\right) \approx -3,3$.
$\quad$
donc si $0<x<\ln \left(2+\sqrt{5}\right)$ alors $0> f(x)$, soit $f(x)< 0$.
Sur l’intervalle $\left]0;\ln \left(2+\sqrt{5}\right)\right[$ on a $f(x)<0$.
Sur l’intervalle $\left[\ln \left(2+\sqrt{5}\right);+\infty\right[$, la fonction $f$ est continue (car dérivable) et strictement croissante.
De plus $f\left(\ln \left(2+\sqrt{5}\right)\right) \approx -3,3<0$ et $\lim\limits_{x \to +\infty} f(x)=+\infty$.
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires) l’équation $f(x)=0$ possède une unique solution $\alpha$ sur l’intervalle $\left[\ln \left(2+\sqrt{5}\right);+\infty\right[$.
Ainsi l’équation $f(x)=0$ possède une unique solution sur l’intervalle $[0;+\infty[$.
$\quad$ - On considère l'algorithme suivant où les variables $a$, $b$ et $m$ sont des nombres réels : $$\begin{array}{|l|}\hline \text{Tant que } b - a > 0,1 \text{faire:}\\ \hspace{1cm} m \gets \dfrac{a+b}{2} \\ \hspace{1cm}\text{ Si } \text{e}^m + \text{e}^{-m} - 4m - 2 > 0 \text{, alors:}\\ \hspace{2cm} b \gets m \\ \hspace{1cm}\text{Sinon :}\\ \hspace{2cm} a\gets m \\ \hspace{1cm}\text{Fin Si }\\ \text{Fin Tant que }\\ \hline \end{array}$$
- Avant l'exécution de cet algorithme, les variables $a$ et $b$ contiennent respectivement les valeurs $2$ et $3$. Que contiennent-elles à la fin de l'exécution de l'algorithme ? On justifiera la réponse en reproduisant et en complétant le tableau ci-contre avec les différentes valeurs prises par les variables, à chaque étape de l'algorithme. $$ \begin{array}{|c|c|c|c|}\hline m & a & b & b - a \\ \hline &2& 3 &1\\ \hline 2,5 &&&\\ \hline \ldots &\ldots&\ldots&\\ \hline ~ &&&\\ \hline \end{array}$$ $$\begin{array}{|c|c|c|c|}
- Comment peut-on utiliser les valeurs obtenues en fin d'algorithme à la question précédente ? On a $f(2)\approx -2,48$ et $f(3)\approx 6,14$.
\hline
m&a&b&b-a\\
\hline
&2&3&1\\
\hline
2,5&2&2,5&0,5\\
\hline
2,25&2,25&2,5&0,25\\
\hline
2,375&2,375&2,5&0,125\\
\hline
2,4375&2,4375&2,5&0,0625\\
\hline
\end{array}$$
À la fin de l’exécution de l’algorithme on a $a=2,437~5$ et $b=2,5$.
$\quad$
Par conséquent $\alpha$ appartient à l’intervalle $]2;3[$.
L’algorithme (de dichotomie) précédent nous fournit un encadrement d’amplitude au plus $0,1$ de cette valeur.
Donc $2,437~5 <\alpha < 2,5$.
$\quad$ - La Gateway Arch, édifiée dans la ville de Saint-Louis aux États-Unis, a l'allure ci-contre. Son profil peut être approché par un arc de chaînette renversé dont la largeur est égale à la hauteur.
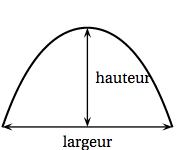
La largeur de cet arc, exprimée en mètre, est égale au double de la solution strictement positive de l'équation : \[\left(E'\right) : \text{e}^{\frac{t}{39}} + \text{e}^{-\frac{t}{39}} - 4\frac{t}{39} - 2 = 0.\] Donner un encadrement de la hauteur de la Gateway Arch. D’après la question précédente la solution de l’équation $(E’)$ vérifie :
La hauteur de la chaînette est $\dfrac{1}{2}\left(\text{e}^x+\text{e}^{-x}-2\right)$.
On veut donc résoudre :
$\begin{align*} 2x=\dfrac{1}{2}\left(\text{e}^x+\text{e}^{-x}-2\right)&\iff 4x=\text{e}^x+\text{e}^{-x}-2 \\
&\iff \text{e}^x+\text{e}^{-x}-4x-2 = 0\end{align*}$
$\quad$
$2,437~5< \dfrac{t}{39}<2,5 \iff 95,062~5<t<97,5$.
Un encadrement de la largeur de cet arc est donc $190,125<2t<195$.
$\quad$ donc la hauteur de l'arche est comprise entre 190 et 195 mètres.
- Vues: 33230
