Baccalauréat S (obligatoire) Polynésie 5 septembre 2017 - Correction Exercice 1

Page 2 sur 8: Correction Exercice 1

Correction de l'exercice 1 (6 points)

Commun à tous les candidats

 

Un parc d'attraction propose à son public un tout nouveau grand huit. Pour des raisons de sécurité, son accès n'est autorisé qu'aux personnes dont la taille est supérieure ou égale à 1,40 m et dont l'âge est compris entre 10 et 70 ans. Des études statistiques sont menées pour évaluer l'affluence et la satisfaction des visiteurs pour ce manège.
On arrondira, si nécessaire, les probabilités à  $10^{-4}$.

1. 1. La taille en centimètres d'un visiteur du parc, choisi au hasard, est modélisée par la variable aléatoire $T$ qui suit la loi normale d'espérance $165$ et d'écart-type $20$. Quelle est la probabilité qu'un visiteur ait la taille requise pour accéder à ce grand huit?
   On veut calculer :
   $P(T\geqslant 140) = 0,5+P(140 \leqslant T \leqslant 165) \approx 0,894~4$.
   La probabilité qu’un visiteur ait la taille requise pour accéder à ce grand huit est environ $0,894~4$.
   $\quad$
   Ou directement :

    

   2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
   Avec une calculatrice de type TI

   $$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$

   $$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
   2. L'âge d'un visiteur du parc, choisi au hasard, est modélisé par la variable aléatoire $X$ qui suit la loi normale d'espérance $30$ et d'écart-type $17$. Quelle est la probabilité qu'un visiteur ait l'âge requis pour accéder à ce grand huit ?
   On veut calculer :
   $P(10 \leqslant X \leqslant 70) \approx 0,871~0$
   

   2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
   Avec une calculatrice de type TI

   $$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$

   $$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$

    

   La probabilité qu’un visiteur ait l’âge requis pour accéder à ce grand huit est environ $0,871~0$.
   $\quad$
   
   3. Les études menées permettent d'établir que 89 % des visiteurs ont la taille exigée, 87 % ont l'âge requis mais 8 % n'ont ni la taille, ni l'âge obligatoires. Quelle est alors la proportion des visiteurs vérifiant les conditions requises pour essayer la nouvelle attraction ?
   On appelle $A$ l’événement “le visiteur à l’âge requis” et $B$ l’événement “le visiteur à la taille requise”.
   On sait donc que $p(A\cup B) = 1-0,08=0,92$
   De plus $P(A\cup B)=P(A)+P(B)-P(A\cap B)$
   $\iff 0,92=0,89+0,87-P(A\cap B)$
   $\iff P(A\cap B)=0,84$
   $84\%$ des visiteurs vérifient donc les 2 conditions.
   $\quad$
2. Un sondage est réalisé à la sortie du grand huit et révèle que 25 % des personnes ont attendu moins de 30 min avant de pouvoir essayer le manège. Parmi elles, 95 % sont satisfaites de l'attraction. En revanche, 22 % des personnes ayant attendu plus de $30$~min ne sont pas satisfaites de l'attraction. On choisit au hasard un visiteur à sa sortie du grand huit. On note $A$ l'évènement « le visiteur a attendu plus de $30$min » et $S$ l'évènement « le visiteur est satisfait de l'attraction ».
   1. Montrer que la probabilité qu'un visiteur soit satisfait de l'attraction vaut 0,8225.
   On peut représenter la situation à l’aide de l’arbre pondéré suivant :
   
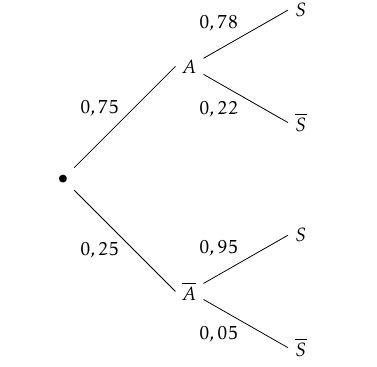
   D’après la formule des probabilités totales on a :
   $\begin{array}{c} P(S)&=P(S\cap A)+P\left(S\cap \overline{A}\right) \\
   &=0,75 \times 0,78+0,25\times 0,95 \\
   &=0,822~5
   \end{array}$
   $\quad$
   
   2. Le directeur rencontre un visiteur insatisfait. Quelle est la probabilité que ce visiteur ait attendu moins de $30$ min ?
   On veut calculer la probabilité :
   $\begin{array}{c} P_{\overline{S}}\left(\overline{A}\right) &=\dfrac{P\left(\overline{S}\cap\overline{A}\right)}{P\left(\overline{S}\right)} \\
   &=\dfrac{0,25\times 0,05}{1-0,822~5} \\
   &\approx 0,070~4
   \end{array}$
   La probabilité que ce visiteur ait attendu moins de $30$ minutes est environ $0,070~4$.
   $\quad$
3. Le directeur est soucieux de savoir si le temps d'attente, plus important les jours de grande affluence, remet en cause le taux de satisfaction des visiteurs. Pour cela, on interroge $200$ personnes au hasard à la sortie du grand huit. Parmi elles, $46$ se disent insatisfaites. Le directeur peut-il être rassuré ?
On a $n=200 \geqslant 30$ et $p=0,822~5$ donc $np=164,5 \geqslant 5$ et $n(1-p)=35,5 \geqslant 5$
Un intervalle de fluctuation asymptotique au seuil de $95\%$ de la proportion de visiteurs satisfaits est donc :
$\begin{array}{c} I_{200}&=\left[0,822~5-1,96\sqrt{\dfrac{0,822~5\times 0,177~5}{200}};0,822~5+1,96\sqrt{\dfrac{0,822~5\times 0,177~5}{200}}\right] \\
&\approx [0,655~0;0,990~0]
\end{array}$
La fréquence observée de visiteurs satisfaits est donc $f=\dfrac{200-46}{200}=0,77 \in I_{200}$.
Le directeur peut donc être rassuré.
$\quad$